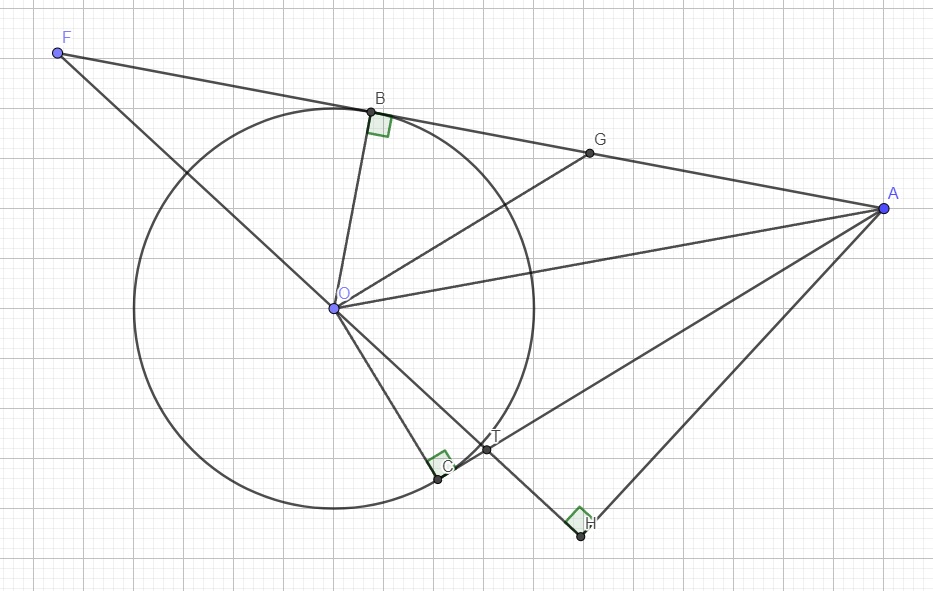
Cho (O;K). Từ A ở ngoài đường tròn vẽ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Vẽ cát tuyến (d) qua A cắt (O) tại M và N (M nằm giữa A và N). Gọi H là trugn điểm MN, OH cắt AC tại K.
a. CM tứ giác ABOC nội tiếp đường tròn. Từ đó suy ra 5 điểm A, B, O, H, C cùng thuộc 1 đtr.
b. CM \(AB^2=AM.AN\) (1)
KC. KA = KH. KO (2)
c. đường thẳng AO cắt đường tròn (O) tại điểm E. CM E cách đều AB, AC và BC.
d. đường thẳng qua O cắt AB, AC lần lượt tại F và T. XĐ vị trí A trên (d) để diện tích AFT min.
(Bày giúp em ý 2 câu b, câu c, câu d em cảm ơn ạ)
(Thầy NVL rảnh giải giúp em - nhớ chi tiết chút em đỡ làm phiền thầy)
Em kiểm tra lại đề câu d, điểm A đã cố định nên đề ko thể là xác định vị trí A được, chỉ có xác định vị trí d qua O sao cho diện tích tam giác kia min thôi
a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp đường tròn đường kính OA(1)
ΔOMN cân tại O
mà OH là trung tuyến
nên OH vuông góc MN
=>OH vuông góc HA
=>H nằm trên đường tròn đường kính OA(2)
Từ (1), (2) suy ra O,H,B,A,C cùng nằm trên đường tròn đường kính AO
b: Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AN*AM
Xét ΔKCO vuông tại C và ΔKHA vuông tại H có
góc K chung
=>ΔKCO đồng dạng với ΔKHA
=>KC/KH=KO/KA
=>KC*KA=KO*KH
c: góc ABE+góc OBE=90 độ
góc CBE+góc OEB=90 độ
mà góc OBE=góc OEB
nên góc ABE=góc CBE
=>BE là phân giác của góc ABC
mà AE là phan giác góc BAC
nên E cách đều AB,BC,AC
d.
Qua O kẻ đường thẳng song song AC cắt AB tại G, kẻ AH vuông góc TF
Do O, A, B, C cố định nên G cố định \(\Rightarrow S_{OAG}\) cố định
Áp dụng Talet: \(\dfrac{AG}{AF}=\dfrac{TO}{TF}\) \(\Rightarrow\dfrac{\dfrac{1}{2}OB.AG}{\dfrac{1}{2}OB.AF}=\dfrac{\dfrac{1}{2}AH.TO}{\dfrac{1}{2}AH.TF}\)
\(\Rightarrow\dfrac{S_{OAG}}{S_{OAF}}=\dfrac{S_{OAT}}{S_{AFT}}\Rightarrow S_{OAG}=\dfrac{S_{OAF}.S_{OAT}}{S_{AFT}}\le\dfrac{\left(S_{OAF}+S_{OAT}\right)^2}{4S_{AFT}}=\dfrac{S_{AFT}^2}{4S_{AFT}}=\dfrac{S_{AFT}}{4}\)
\(\Rightarrow S_{AFT}\ge4S_{OAG}\)
Dấu "=" xảy ra khi và chỉ khi \(S_{OAF}=S_{OAT}\Rightarrow AF=AT\)
\(\Rightarrow AO\) là trung trực FT hay \(d\perp AO\)