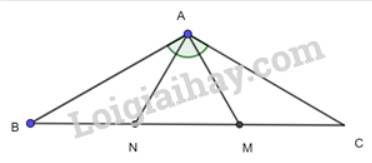
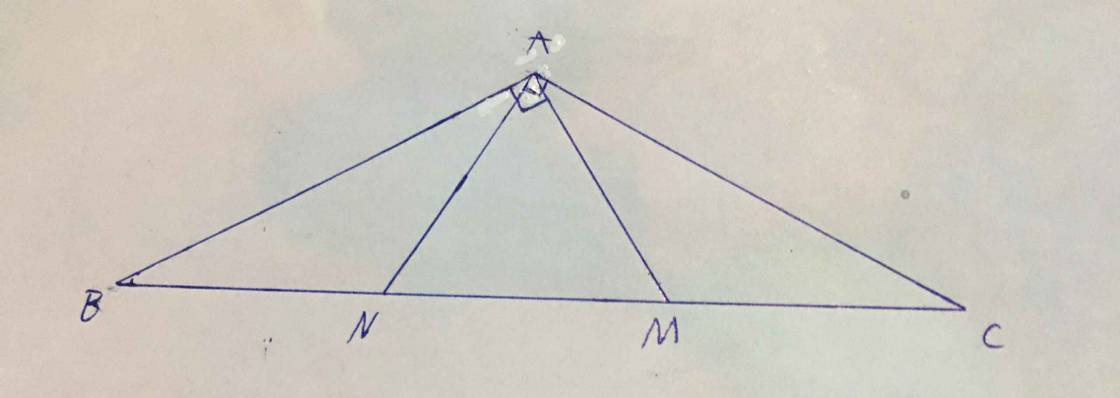
\(\Delta\)ABC can tại A (A<45 độ) .M\(\in\\\)BC , MH//AB(H thuộc AC),MI//AC(I thuộc AB) ,HI \(\perp\)MN,HI là đường trung trực của MN,NH cắt AB tại D
a)tam giác AIH=tam giác MHI
b)AI=HC
c)IN=IB
d)chu vi tam giác ADH không phụ thuộc vào vị trí điểm M.