\(\dfrac{1}{2}\)+ \(\dfrac{1}{12}\)

Những câu hỏi liên quan
VÒNG 2Bài 1: Mèo con nhanh nhẹndfrac{1}{2} + dfrac{1}{12}2 + dfrac{1}{6}dfrac{1}{20}1 - dfrac{1}{9} dfrac{1}{15} + dfrac{2}{15}dfrac{1}{2} + dfrac{2}{3}dfrac{7}{12}dfrac{4}{12} dfrac{9}{14}+ dfrac{1}{14}1 + dfrac{1}{6}dfrac{1}{4} - dfrac{1}{5}dfrac{1}{3} - dfrac{2}{9} dfrac{3}{2} + dfrac{2}{3}dfrac{1}{5}1 - dfrac{8}{9} dfrac{5}{7}1 - dfrac{2}{3}dfrac{1}{3} + dfrac{5}{9}
Đọc tiếp
VÒNG 2
Bài 1: Mèo con nhanh nhẹn
| \(\dfrac{1}{2}\) + \(\dfrac{1}{12}\) | 2 + \(\dfrac{1}{6}\) | \(\dfrac{1}{20}\) | 1 - \(\dfrac{1}{9}\) | |
| \(\dfrac{1}{15}\) + \(\dfrac{2}{15}\) | \(\dfrac{1}{2}\) + \(\dfrac{2}{3}\) | \(\dfrac{7}{12}\) | \(\dfrac{4}{12}\) | |
| \(\dfrac{9}{14}\)+ \(\dfrac{1}{14}\) | 1 + \(\dfrac{1}{6}\) | \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) | \(\dfrac{1}{3}\) - \(\dfrac{2}{9}\) | |
| \(\dfrac{3}{2}\) + \(\dfrac{2}{3}\) | \(\dfrac{1}{5}\) | 1 - \(\dfrac{8}{9}\) | ||
| \(\dfrac{5}{7}\) | 1 - \(\dfrac{2}{3}\) | \(\dfrac{1}{3}\) + \(\dfrac{5}{9}\) |
Tính (theo mẫu).Mẫu: dfrac{1}{2}-dfrac{5}{12}dfrac{6}{12}-dfrac{5}{12}dfrac{6-5}{12}dfrac{1}{12}a) dfrac{3}{4}-dfrac{1}{8} b) dfrac{2}{6}-dfrac{5}{18} c) dfrac{2}{5}-dfrac{3}{20}
Đọc tiếp
Tính (theo mẫu).
| Mẫu: \(\dfrac{1}{2}-\dfrac{5}{12}=\dfrac{6}{12}-\dfrac{5}{12}=\dfrac{6-5}{12}=\dfrac{1}{12}\) |
a) \(\dfrac{3}{4}-\dfrac{1}{8}\) b) \(\dfrac{2}{6}-\dfrac{5}{18}\) c) \(\dfrac{2}{5}-\dfrac{3}{20}\)
a) \(\dfrac{3}{4}-\dfrac{1}{8}=\dfrac{6}{8}-\dfrac{1}{8}=\dfrac{6-1}{8}=\dfrac{5}{8}\)
b) \(\dfrac{2}{6}-\dfrac{5}{18}=\dfrac{6}{18}-\dfrac{5}{18}=\dfrac{6-5}{18}=\dfrac{1}{18}\)
c) \(\dfrac{2}{5}-\dfrac{3}{20}=\dfrac{8}{20}-\dfrac{3}{20}=\dfrac{8-3}{20}=\dfrac{5}{20}=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
1/ \(\dfrac{x+4}{4}+\dfrac{3x-7}{5}=\dfrac{7x+2}{20}\)
2/ \(\dfrac{x}{6}+\dfrac{1-3x}{9}=\dfrac{-x+1}{12}\)
3/ \(\dfrac{x-3}{3}-\dfrac{x+2}{12}=\dfrac{2x-1}{4}\)
4/ \(\dfrac{x-2}{4}-\dfrac{2x+3}{3}=\dfrac{x+6}{12}\)
5/ \(\dfrac{2x-1}{12}-\dfrac{3-x}{18}=\dfrac{-1}{36}\)
1: Ta có: \(\dfrac{x+4}{4}+\dfrac{3x-7}{5}=\dfrac{7x+2}{20}\)
\(\Leftrightarrow5x+20+12x-28=7x+2\)
\(\Leftrightarrow17x-7x=2+8=10\)
hay x=1
2: Ta có: \(\dfrac{x}{6}+\dfrac{1-3x}{9}=\dfrac{-x+1}{12}\)
\(\Leftrightarrow\dfrac{6x}{36}+\dfrac{4\left(1-3x\right)}{36}=\dfrac{3\left(-x+1\right)}{36}\)
\(\Leftrightarrow6x+4-12x=-3x+3\)
\(\Leftrightarrow-6x+3x=3-4\)
hay \(x=\dfrac{1}{3}\)
3: Ta có: \(\dfrac{x-3}{3}-\dfrac{x+2}{12}=\dfrac{2x-1}{4}\)
\(\Leftrightarrow4x-12-x-2=6x-3\)
\(\Leftrightarrow3x-14-6x+3=0\)
\(\Leftrightarrow-3x=11\)
hay \(x=-\dfrac{11}{3}\)
Đúng 0
Bình luận (0)
4: Ta có: \(\dfrac{x-2}{4}-\dfrac{2x+3}{3}=\dfrac{x+6}{12}\)
\(\Leftrightarrow3x-6-8x-12=x+6\)
\(\Leftrightarrow-5x-x=6+18\)
hay x=-4
5: Ta có: \(\dfrac{2x-1}{12}-\dfrac{3-x}{18}=\dfrac{-1}{36}\)
\(\Leftrightarrow6x-3+2x-6=-1\)
\(\Leftrightarrow8x=8\)
hay x=1
Đúng 0
Bình luận (0)
Bài 6 tính
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\)
\(F=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(G=\dfrac{12}{84}+\dfrac{12}{210}+\dfrac{12}{390}+...+\dfrac{12}{210}\)
+) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\)
\(\Rightarrow2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\right)\)
\(\Rightarrow A=1-\dfrac{1}{2^{10}}=\dfrac{2^{10}-1}{2^{10}}\)
Vậy \(A=\dfrac{2^{10}-1}{2^{10}}\)
+) \(F=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(\Rightarrow\dfrac{1}{2}F=\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+...+\dfrac{1}{380}\)
\(=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{19.20}=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
\(=\dfrac{1}{5}-\dfrac{1}{20}=\dfrac{3}{20}\Rightarrow F=\dfrac{3}{20}:\dfrac{1}{2}=\dfrac{3}{10}\)
Vậy \(F=\dfrac{3}{10}\)
+) \(G=\dfrac{12}{84}+\dfrac{12}{210}+\dfrac{12}{390}+...+\dfrac{12}{2100}\)
\(=\dfrac{4}{28}+\dfrac{4}{70}+\dfrac{4}{130}+...+\dfrac{4}{700}=\dfrac{4}{4.7}+\dfrac{4}{7.10}+...+\dfrac{4}{25.28}\)
\(=\dfrac{4}{3}.\left(\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{25.28}\right)\)
\(=\dfrac{4}{3}.\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}.\left(\dfrac{1}{4}-\dfrac{1}{28}\right)=\dfrac{4}{3}.\dfrac{3}{14}=\dfrac{2}{7}\)
Vậy \(G=\dfrac{2}{7}\)
Đúng 0
Bình luận (0)
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\)
\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\)
\(2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{10}}\right)\)
\(A=1-\dfrac{1}{2^{10}}=\dfrac{1024-1}{1024}=\dfrac{1023}{1024}\)
\(F=\dfrac{1}{15}+\dfrac{1}{21}+\dfrac{1}{28}+...+\dfrac{1}{190}\)
\(=\dfrac{2}{30}+\dfrac{2}{42}+\dfrac{2}{56}+...+\dfrac{2}{380}\)
\(=\dfrac{2}{5.6}+\dfrac{2}{6.7}+\dfrac{2}{7.8}+...+\dfrac{2}{19.20}\)
\(=2\left(\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{19.20}\right)\)
\(=2\left(\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)
\(=2\left(\dfrac{1}{5}-\dfrac{1}{20}\right)=2.\dfrac{3}{20}=\dfrac{3}{10}\)
\(G=\dfrac{12}{84}+\dfrac{12}{210}+\dfrac{12}{390}+...+\dfrac{12}{2100}\)
\(=\dfrac{4}{28}+\dfrac{4}{70}+\dfrac{4}{130}+...+\dfrac{4}{700}\)
\(=\dfrac{4}{4.7}+\dfrac{4}{7.10}+\dfrac{4}{10.13}+...+\dfrac{4}{25.28}\)
\(=\dfrac{4}{3}\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}\left(\dfrac{1}{4}-\dfrac{1}{28}\right)\)
\(=\dfrac{4}{3}.\dfrac{3}{14}=\dfrac{2}{7}\)
Đúng 0
Bình luận (0)
Bài 1: tính M :N biết:
a) Ndfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+.......+dfrac{1}{2007}+dfrac{1}{2008} và M dfrac{2007}{1}+dfrac{2006}{2}+dfrac{2005}{3}+.......+dfrac{2}{2006}+dfrac{1}{2007}
b) M dfrac{1}{11.13}+dfrac{1}{13.15}+dfrac{1}{15.17}+.......+dfrac{1}{31.33}+dfrac{1}{33.35} và N dfrac{12}{11.13.15}+dfrac{12}{13.15.17}+dfrac{12}{15.17.19}+.....+dfrac{12}{31.33.35}
Đọc tiếp
Bài 1: tính M :N biết:
a) N=\(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+.......+\dfrac{1}{2007}+\dfrac{1}{2008}\) và M= \(\dfrac{2007}{1}+\dfrac{2006}{2}+\dfrac{2005}{3}+.......+\dfrac{2}{2006}+\dfrac{1}{2007}\)
b) M= \(\dfrac{1}{11.13}+\dfrac{1}{13.15}+\dfrac{1}{15.17}+.......+\dfrac{1}{31.33}+\dfrac{1}{33.35}\) và N= \(\dfrac{12}{11.13.15}+\dfrac{12}{13.15.17}+\dfrac{12}{15.17.19}+.....+\dfrac{12}{31.33.35}\)
a, Theo bài ra ta có:
\(M=\dfrac{2007}{1}+1+\dfrac{2006}{2}+1+.......+\dfrac{2}{2006}+1+\dfrac{1}{2007}+1-2007\)
( Ta thêm 1 vào mỗi một số hạng trong M nên phải bớt đi 2017 vì có 2017 số hạng ) ;'
\(=>M=2008+\dfrac{2008}{2}+\dfrac{2008}{3}+......+\dfrac{2008}{2007}+\dfrac{2008}{2007}-2007\)
\(=>M=\dfrac{2008}{2}+\dfrac{2008}{3}+\dfrac{2008}{4}+.....+\dfrac{2008}{2006}+\dfrac{2008}{2007}+1\)
Ta thấy xuất hiện 2008 chung nên đặt ra ngoài ta có:
\(=>M=2008\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2006}+\dfrac{1}{2007}+\dfrac{1}{2008}\right)\)
\(=>M:N=2008\)
Câu b đợi 1 chút nha.......
Đúng 0
Bình luận (2)
b, \(M=\dfrac{1}{11.13}+\dfrac{1}{13.15}+...+\dfrac{1}{31.33}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{11.13}+\dfrac{2}{13.15}+...+\dfrac{2}{31.33}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{11}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{15}+...+\dfrac{1}{31}-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{11}-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{33}\)
\(N=\dfrac{12}{11.13.15}+\dfrac{12}{13.15.17}+...+\dfrac{12}{31.33.35}\)
\(=3\left(\dfrac{4}{11.13.15}+\dfrac{4}{13.15.17}+...+\dfrac{4}{31.33.35}\right)\)
\(=3\left(\dfrac{1}{11.13}-\dfrac{1}{13.15}+\dfrac{1}{13.15}-\dfrac{1}{15.17}+...+\dfrac{1}{31.33}-\dfrac{1}{33.35}\right)\)
\(=3\left(\dfrac{1}{11.13}-\dfrac{1}{33.35}\right)\)
\(=\dfrac{92}{5005}\)
\(\Rightarrow M:N=\dfrac{1}{33}:\dfrac{92}{5005}=\dfrac{455}{276}\)
Vậy...
Đúng 0
Bình luận (1)
\(\dfrac{-29}{12}+1+\dfrac{19}{-12}\)\(\le\)x\(\le\dfrac{-1}{3}+\dfrac{3}{4}+\dfrac{7}{12}\)
\(\dfrac{-5}{3}+1+\dfrac{1}{-3}\le x\le\dfrac{8}{10}+\dfrac{1}{5}+2\)
Bài 2: Tính hợp lý:
\(A=\dfrac{63636337-37373763}{1+2+3+...+2006}\)
\(B=1\dfrac{6}{41}\left(\dfrac{12+\dfrac{12}{19}-\dfrac{12}{37}-\dfrac{12}{53}}{3+\dfrac{1}{3}-\dfrac{3}{37}-\dfrac{3}{53}}:\dfrac{4+\dfrac{4}{17}+\dfrac{4}{19}+\dfrac{4}{2006}}{5+\dfrac{5}{17}+\dfrac{5}{19}+\dfrac{5}{2006}}\right)\dfrac{124242423}{237373735}\)
\(A=\dfrac{636363\cdot37-373737\cdot63}{1+2+3+...+2006}\)
\(=\dfrac{37^2\cdot3^3\cdot7^2\cdot13-37^2\cdot3^3\cdot7^2\cdot13}{\left(2006+1\right)\cdot1003}\)
=0
Đúng 0
Bình luận (0)
Rút gọn:
\(\sqrt{1+\dfrac{1}{11^2}+\dfrac{1}{12^2}}+\sqrt{1+\dfrac{1}{12^2}+\dfrac{1}{13^2}}+...+1\sqrt{1+\dfrac{1}{\left(n+1\right)^2}+\dfrac{1}{\left(n+2\right)^2}}\)
Em xin lỗi, p.số cuối ở số 1 ở ngoài căn ạ, em đánh lộn:
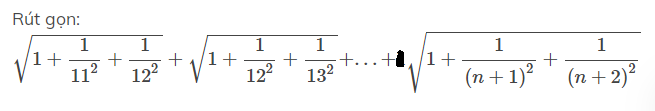
Đúng 0
Bình luận (0)
Áp dụng hằng đẳng thức: \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\) nếu \(a+b+c=0\) là ra
Đúng 0
Bình luận (0)
ĐK: \(n>0\)
Ta có: \(\left(1+\dfrac{1}{n}-\dfrac{1}{n+1}\right)^2\)
\(=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}+2\left(\dfrac{1}{n}-\dfrac{1}{n+1}-\dfrac{1}{n\left(n+1\right)}\right)\)
\(=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}+2.\dfrac{n+1-n-1}{n\left(n+1\right)}\)
\(=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}+0=1+\dfrac{1}{n^2}+\dfrac{1}{\left(n+1\right)^2}\)
Áp dụng:
\(\sqrt{1+\dfrac{1}{11^2}+\dfrac{1}{12^2}}+\sqrt{1+\dfrac{1}{12^2}+\dfrac{1}{13^2}}+...+\sqrt{1+\dfrac{1}{\left(n+1\right)^2}+\dfrac{1}{\left(n+2\right)^2}}\)
\(=\sqrt{\left(1+\dfrac{1}{11}-\dfrac{1}{12}\right)^2}+\sqrt{\left(1+\dfrac{1}{12}-\dfrac{1}{13}\right)^2}+...+\sqrt{\left(1+\dfrac{1}{n+1}-\dfrac{1}{n+2}\right)^2}\)
\(=\left|1+\dfrac{1}{11}-\dfrac{1}{12}\right|+\left|1+\dfrac{1}{12}-\dfrac{1}{13}\right|+...+\left|1+\dfrac{1}{n+1}-\dfrac{1}{n+2}\right|\)
\(=1+\dfrac{1}{11}-\dfrac{1}{12}+1+\dfrac{1}{12}-\dfrac{1}{13}+...+1+\dfrac{1}{n+1}-\dfrac{1}{n+2}\)
\(=\left(n-9\right)+\dfrac{1}{11}-\dfrac{1}{n+2}=n-\dfrac{1}{n+2}-\dfrac{98}{11}\)
Đúng 0
Bình luận (0)
a) \(\dfrac{1}{2}+\dfrac{-1}{-3}-\dfrac{5}{12}< 2x< \dfrac{12}{-31}+\dfrac{136}{31}\)
b) \(\dfrac{-2}{5}< \dfrac{x}{15}< \dfrac{1}{6}\)
HéP :)
`a)1/2+[-1]/[-3]-5/12 < 2x < 12/[-31]+136/31`
`186/372+124/372-155/372 < [744x]/372 < [-144]/372+1632/372`
`186+124-155 < 744x < -144+1632`
`155 < 744x < 1488`
`155:744 < 744x:744 < 1488:744`
`5/24 < x < 2`
Vậy `5/24 < x < 2`
__________________________________________________
`b)[-2]/5 < x/15 < 1/6`
`[-12]/30 < [2x]/30 < 5/30`
`-12 < 2x < 5`
`-12:2 < 2x:2 < 5:2`
`-6 < x < 5/2`
Vậy `-6 < x < 5/2`
Đúng 2
Bình luận (0)
Giải:
a) x - \(\dfrac{9}{25}\)= \(\dfrac{16}{25}\)
x = \(\dfrac{16}{25}\)+\(\dfrac{9}{25}\)
x = \(\dfrac{25}{25}\)
x = 1
b) \(\dfrac{-12}{30}\)<\(\dfrac{x}{30}\)<\(\dfrac{5}{30}\)
=> x có thể bằng \(\dfrac{-11}{30}\) đến \(\dfrac{4}{30}\)
=> x bằng -5; -4; -3; -2; -1;0;1;2
Đúng 0
Bình luận (2)
Giải phương trình:
a) \(\dfrac{x+5}{3x-6}-\dfrac{1}{2}=\dfrac{2x-3}{2x-4}\)
b) \(\dfrac{12}{1-9x^2}=\dfrac{1-3x}{1+3x}-\dfrac{1+3x}{1-3x}\)
c) \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
a) Ta có: \(\dfrac{x+5}{3x-6}-\dfrac{1}{2}=\dfrac{2x-3}{2x-4}\)
\(\Leftrightarrow\dfrac{2\left(x+5\right)}{6\left(x-2\right)}-\dfrac{3\left(x-2\right)}{6\left(x-2\right)}=\dfrac{3\left(2x-3\right)}{6\left(x-2\right)}\)
Suy ra: \(2x+5-3x+6=6x-9\)
\(\Leftrightarrow-x+11-6x+9=0\)
\(\Leftrightarrow20-7x=0\)
\(\Leftrightarrow7x=20\)
hay \(x=\dfrac{20}{7}\)(thỏa ĐK)
Vậy: \(S=\left\{\dfrac{20}{7}\right\}\)
Đúng 0
Bình luận (0)






























