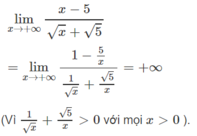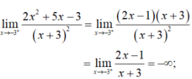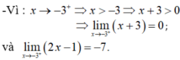tính giới hạn y= 2sin x+cõx+5x

Những câu hỏi liên quan
Tính giới hạn
lim
x
→
−
3
−
2
x
2
−
x
+
5
x
+
3
A.
lim...
Đọc tiếp
Tính giới hạn lim x → − 3 − 2 x 2 − x + 5 x + 3
A. lim x → − 3 − 2 x 2 − x + 5 x + 3 = + ∞
B. lim x → − 3 − 2 x 2 − x + 5 x + 3 = 2
C. lim x → − 3 − 2 x 2 − x + 5 x + 3 = − ∞
D. lim x → − 3 − 2 x 2 − x + 5 x + 3 = − 2
Đáp án C
lim x → − 3 − 2 x 2 − x + 5 x + 3 = − ∞
Đúng 0
Bình luận (0)
Tính các giới hạn sau: lim x → + ∞ x - 5 x + 5
Tính các giới hạn sau: lim x → 5 x - 5 x - 5
Tính giới hạn I = limx→1 (x2 − 5x + 8 / x + 1)
\(=\dfrac{1-5+8}{1+1}=\dfrac{4}{2}=2\)
Đúng 0
Bình luận (0)
Tính các giới hạn sau: lim x → - 3 + 2 x 2 + 5 x - 3 ( x + 3 ) 2
tính giá trị của giới hạn \(\lim\limits_{x\rightarrow-\infty}\left(x+\sqrt{x^2+5x}\right)\)
\(\lim\limits_{x\rightarrow-\infty}\left(x+\sqrt{x^2+5x}\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{-5x}{x-\sqrt{x^2+5x}}\\ =\lim\limits_{x\rightarrow-\infty}\dfrac{5}{-1-\sqrt{1+\dfrac{5}{x}}}=-\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
Tính giới hạn: \(A=\lim\limits_{x\rightarrow0}\dfrac{\left(x^2+2017\right)\sqrt[5]{1-5x}-2017}{x}\)
\(A=\lim\limits_{x\rightarrow0}\dfrac{\left(x^2+2017\right)\left(\sqrt[5]{1-5x}-1\right)+x^2}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-\dfrac{5x\left(x^2+2017\right)}{\sqrt[5]{\left(1-5x\right)^4}+\sqrt[5]{\left(1-5x\right)^3}+\sqrt[5]{\left(1-5x\right)^2}+\sqrt[5]{1-5x}+1}+x^2}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(-\dfrac{5\left(x^2+2017\right)}{\sqrt[5]{\left(1-5x\right)^4}+\sqrt[5]{\left(1-5x\right)^3}+\sqrt[5]{\left(1-5x\right)^2}+\sqrt[5]{1-5x}+1}+x\right)\)
\(=-2017\)
Đúng 2
Bình luận (0)
dễ thấy hàm số trên có dạng 0/0
áp dụng quy tắc l'Hôpital
\(A=_{\lim\limits_{x\rightarrow0}\dfrac{\left(x^2+2017\right)\sqrt[5]{1-5x}-2017}{x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\left(x^2+2017\right)\sqrt[5]{1-5x}-2017\right)'}{\left(x\right)'}}\)
\(A=\lim\limits_{x\rightarrow0}\dfrac{-x^2-2017}{\sqrt[5]{\left(1-5x\right)^4}}+2x\sqrt[5]{1-5x}=\dfrac{-2017}{1}=-2017\)
Đúng 0
Bình luận (0)
tính các giới hạn sau:
a. \(lim\dfrac{\sqrt{x+1}-x+1}{x^2-5x+6}\)
x->3
b. \(lim\left|x^3-3x\right|\)
x->-2
Câu a.
\(^{lim}_{x\rightarrow3}\dfrac{\sqrt{x+1}-x+1}{x^2-5x+6}\)
Nhân liên hợp ta đc:
\(^{lim}_{x\rightarrow3}\dfrac{x+1-\left(x-1\right)^2}{(x^2-5x+6)\cdot\left(\sqrt{x+1}+x-1\right)}\)
\(=^{lim}_{x\rightarrow3}\dfrac{-x^2+3x}{\left(x-3\right)\left(x-2\right)\left(\sqrt{x+1}+x-1\right)}\)
\(=^{lim}_{x\rightarrow3}\dfrac{-x}{\left(x-2\right)\cdot\left(\sqrt{x+1}+x-1\right)}\)
\(=\dfrac{-3}{\left(3-2\right)\cdot\left(\sqrt{3+1}+3-1\right)}=-\dfrac{3}{4}\)
Đúng 1
Bình luận (0)
Câu b.
\(^{lim}_{x\rightarrow-2}\left|x^3-3x\right|\)
\(=\left|\left(-2\right)^3-3\cdot\left(-2\right)\right|=\left|-2\right|=2\)
Câu này đơn giản chỉ thay số thôi nhé, nó ở dạng đa thức nữa!
Đúng 1
Bình luận (0)
Tính giới hạn
Lim\(x = {5x^2-7x+1 {} \over3-2x}\)