\(E=\dfrac{tan64^o}{cot26^o}-1\)

Những câu hỏi liên quan
\(\frac{\sin^390^o-\cot^330^o-\cos^245^o+\tan20^o}{2\sqrt{7}+\sin108^o\cos32^o\tan64^o}\)
Bài 2: ( chỉ ghi kết quả )
a) Tìm x biết : \(\dfrac{1}{2-\dfrac{3}{4+\dfrac{5}{6-\dfrac{7}{8+\dfrac{9}{10}}}}}=\dfrac{1}{x+\dfrac{1}{3+\dfrac{1}{5}}}+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{2}}}\)
b) Tính: ( kết quả lấy 4 chữ số thập phân)
\(P=\dfrac{\sin^390^0-\cot^330^0-\cos^245^0+\tan20^0}{2\sqrt{7}+\sin108^0\cos32^0\tan64^0}\)
\(\dfrac{1}{2-\dfrac{3}{4+\dfrac{5}{6-\dfrac{7}{8+\dfrac{9}{10}}}}}=\dfrac{1}{x+\dfrac{1}{3+\dfrac{1}{5}}}+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{2}}}\\ \Leftrightarrow\dfrac{767}{1070}=\dfrac{1}{x+\dfrac{5}{16}}+\dfrac{3}{5}\\ \Leftrightarrow\dfrac{25}{214}=\dfrac{1}{x+\dfrac{5}{16}}\\ \Rightarrow x+\dfrac{5}{16}=\dfrac{214}{25}\Rightarrow x=\dfrac{3299}{400}\)
Đúng 0
Bình luận (0)
1;tính A dfrac{1}{cos290^o}+dfrac{1}{sqrt{3}sin250^o}
2; tính B (1+tan 20o) ( 1+tan25o)
3; tính tan9o-tan27o-tan63o+ tan81o
4; tính D sin^2dfrac{pi}{9}+sin^2dfrac{2pi}{9}+sindfrac{pi}{9}sindfrac{2pi}{9}
5; tính E; sindfrac{pi}{32}cosdfrac{pi}{32}cosdfrac{pi}{16}cosdfrac{pi}{8}
Đọc tiếp
1;tính A= \(\dfrac{1}{\cos290^o}+\dfrac{1}{\sqrt{3}\sin250^o}\)
2; tính B = (1+tan 20o) ( 1+tan25o)
3; tính tan9o-tan27o-tan63o+ tan81o
4; tính D= \(\sin^2\dfrac{\pi}{9}+\sin^2\dfrac{2\pi}{9}+\sin\dfrac{\pi}{9}\sin\dfrac{2\pi}{9}\)
5; tính E;= \(\sin\dfrac{\pi}{32}\cos\dfrac{\pi}{32}\cos\dfrac{\pi}{16}\cos\dfrac{\pi}{8}\)
tu 1 diem A ngoai dton (O) ke tiep tuyen AB,Ac den (O) ,duong thang qua A cat (O) tai D,C (Dnam giua A va E) .H la trung diem DE cat BC tai K
cm\(\dfrac{2}{AK}=\dfrac{1}{AD}+\dfrac{1}{Ae}\)

\(\text{Chứng minh rằng: }\dfrac{2}{AK}=\dfrac{1}{AD}+\dfrac{1}{AE}\)
➤➤➤ Chứng minh:
➤ Vì H là trung điểm của ED (gt) nên DE = 2HD
Ta có: \(\dfrac{1}{AD}+\dfrac{1}{AE}=\dfrac{AE+AD}{AD\times AE}=\dfrac{\left(AD+DE\right)+AD}{AD\times AE}=\dfrac{2\left(AD+DH\right)}{AD\times AE}=\dfrac{2AH}{AD\times AE}\) (1)
➤ Xét ΔABD và ΔAEB có:
\(\widehat{A_1}\text{ chung}\)
\(\widehat{B_1}=\widehat{E_1}\left(\text{cùng chắn }\stackrel\frown{BD}\right)\)
⇒ ΔABD và ΔAEB (g - g)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\)
\(\Rightarrow AB^2=AD\times AE\) (2)
➤ Vì H là trung điểm của ED (gt) OH ⊥ ED
⇒ O, H, A, B, C cùng thuộc đường tròn đường kính OA
\(\Rightarrow\widehat{H_1}=\widehat{C_1}\)
Mặt khác: 2 tiếp tuyến AB và AC của (O) cắt nhau tại A ⇒ AB = AC
⇒ ΔABC cân tại A
\(\Rightarrow\widehat{C_1}=\widehat{ABC}\)
Suy ra: \(\widehat{H_1}=\widehat{ABK}\)
⇒ ΔABK và ΔAHB (g - g)
\(\Rightarrow\dfrac{AB}{AH}=\dfrac{AK}{AB}\)
\(\Rightarrow AB^2=AH\times AK\) (3)
➤➤ Từ (1), (2), (3) \(\Rightarrow\dfrac{1}{AD}+\dfrac{1}{AE}=\dfrac{2AH}{AH\times AK}=\dfrac{2}{AK}\left(đpcm\right)\)
Đúng 0
Bình luận (1)
Anh Thịnh ơi cứu em với anh sáng e đi học rồiCho hình thang ABCD (AB//CD), O là giao điểm của 2 đường chéo qua O. Kẻ đường thẳng song song với AB cắt DA tại E, BC tại F a) CM:S_{AOD}S_{BOC} b) CM:dfrac{1}{AB}+dfrac{1}{CD}dfrac{2}{EF}c) Gọi K là điểm bất kì thuộc OE. Nêu cách dựng đường thẳng đi qua K chia đôi diện tích DEF
Đọc tiếp
Anh Thịnh ơi cứu em với anh sáng e đi học rồi
Cho hình thang ABCD (AB//CD), O là giao điểm của 2 đường chéo qua O. Kẻ đường thẳng song song với AB cắt DA tại E, BC tại F
a) \(CM:S_{AOD}=S_{BOC}\)
b) \(CM:\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{EF}\)
c) Gọi K là điểm bất kì thuộc OE. Nêu cách dựng đường thẳng đi qua K chia đôi diện tích DEF
Từ O kẻ đường thẳng song song với AB hay như nào vậy bạn.
Đúng 1
Bình luận (0)
a) 2sinleft(x+dfrac{pi}{3}right)+10b) 1+2sinleft(x-30^oright)0c) sqrt{3}+2sinleft(x-dfrac{pi}{6}right)0d) 2sinleft(x+10^oright)+sqrt{3}0e) sqrt{2}+2sinleft(x-15^oright)0f) sqrt{2}sinleft(x-dfrac{pi}{3}right)+10g) 3+sqrt{5}sinleft(x+dfrac{pi}{3}right)0h) 1+sinleft(x-30^oright)0i) 3+sqrt{5}sinleft(x-dfrac{pi}{6}right)0k) 2sqrt{2}sin^2x-sin2x0
Đọc tiếp
a) \(2sin\left(x+\dfrac{\pi}{3}\right)+1=0\)
b) \(1+2sin\left(x-30^o\right)=0\)
c) \(\sqrt{3}+2sin\left(x-\dfrac{\pi}{6}\right)=0\)
d) \(2sin\left(x+10^o\right)+\sqrt{3}=0\)
e) \(\sqrt{2}+2sin\left(x-15^o\right)=0\)
f) \(\sqrt{2}sin\left(x-\dfrac{\pi}{3}\right)+1=0\)
g) \(3+\sqrt{5}sin\left(x+\dfrac{\pi}{3}\right)=0\)
h) \(1+sin\left(x-30^o\right)=0\)
i) \(3+\sqrt{5}sin\left(x-\dfrac{\pi}{6}\right)=0\)
k) \(2\sqrt{2}sin^2x-sin2x=0\)
a: =>2sin(x+pi/3)=-1
=>sin(x+pi/3)=-1/2
=>x+pi/3=-pi/6+k2pi hoặc x+pi/3=7/6pi+k2pi
=>x=-1/2pi+k2pi hoặc x=2/3pi+k2pi
b: =>2sin(x-30 độ)=-1
=>sin(x-30 độ)=-1/2
=>x-30 độ=-30 độ+k*360 độ hoặc x-30 độ=180 độ+30 độ+k*360 độ
=>x=k*360 độ hoặc x=240 độ+k*360 độ
c: =>2sin(x-pi/6)=-căn 3
=>sin(x-pi/6)=-căn 3/2
=>x-pi/6=-pi/3+k2pi hoặc x-pi/6=4/3pi+k2pi
=>x=-1/6pi+k2pi hoặc x=3/2pi+k2pi
d: =>2sin(x+10 độ)=-căn 3
=>sin(x+10 độ)=-căn 3/2
=>x+10 độ=-60 độ+k*360 độ hoặc x+10 độ=240 độ+k*360 độ
=>x=-70 độ+k*360 độ hoặc x=230 độ+k*360 độ
e: \(\Leftrightarrow2\cdot sin\left(x-15^0\right)=-\sqrt{2}\)
=>\(sin\left(x-15^0\right)=-\dfrac{\sqrt{2}}{2}\)
=>x-15 độ=-45 độ+k*360 độ hoặc x-15 độ=225 độ+k*360 độ
=>x=-30 độ+k*360 độ hoặc x=240 độ+k*360 độ
f: \(\Leftrightarrow sin\left(x-\dfrac{pi}{3}\right)=-\dfrac{1}{\sqrt{2}}\)
=>x-pi/3=-pi/4+k2pi hoặc x-pi/3=5/4pi+k2pi
=>x=pi/12+k2pi hoặc x=19/12pi+k2pi
Đúng 1
Bình luận (0)
g) \(3+\sqrt[]{5}sin\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=-\dfrac{3}{\sqrt[]{5}}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin\left[arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)\right]\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\\x+\dfrac{\pi}{3}=\pi-arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}-arcsin\left(-\dfrac{3}{\sqrt[]{5}}\right)+k2\pi\end{matrix}\right.\)
h) \(1+sin\left(x-30^o\right)=0\)
\(\Leftrightarrow sin\left(x-30^o\right)=-1\)
\(\Leftrightarrow sin\left(x-30^o\right)=sin\left(-90^o\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-30^o=-90^0+k360^o\\x-30^o=180^o+90^0+k360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-60^0+k360^o\\x=300^0+k360^o\end{matrix}\right.\)
\(\Leftrightarrow x=-60^0+k360^o\)
Đúng 1
Bình luận (0)
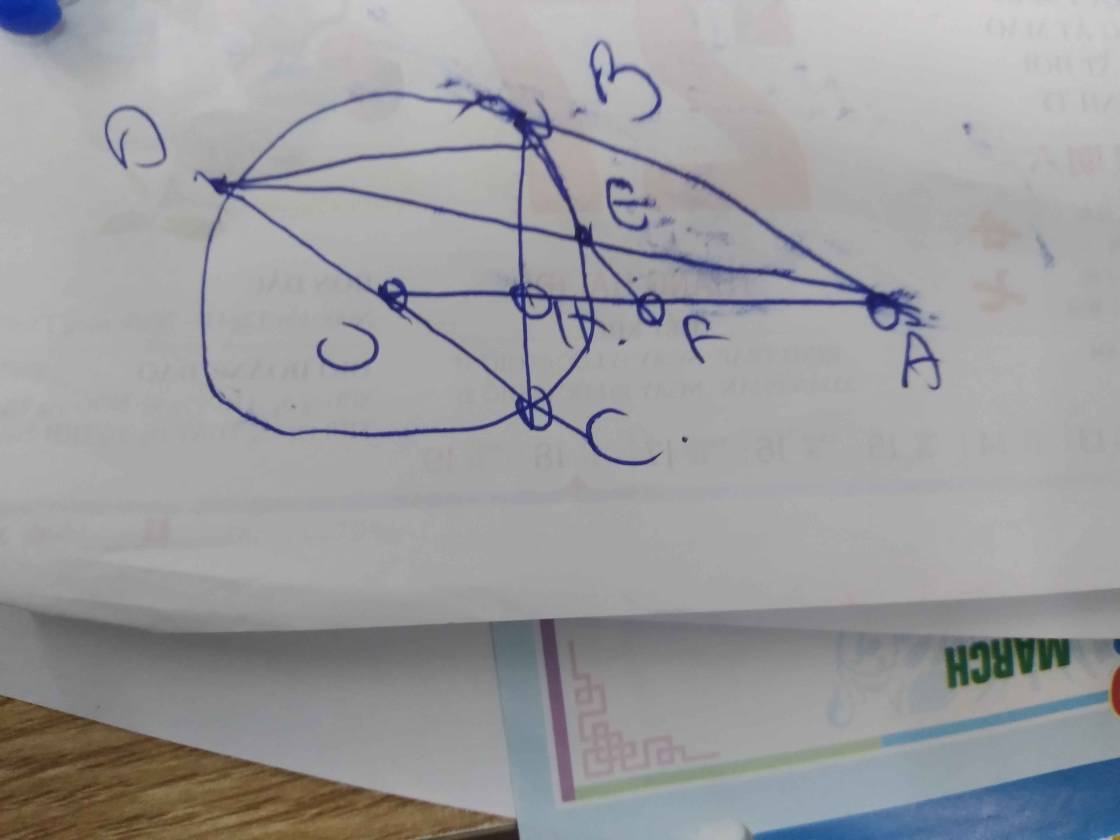
cho đt (O) và A nằm ngoài đt. Từ A kẻ tiếp tuyến AB,AC (B,C là tiếp điểm). Đường thẳng CO cắt (O) tại D (D≠C). AD cắt (O) tại E (E≠A). BE cắt AO tại F, AO cắt BC tại H.
Chứng minh HE vuông góc BF. Và \(\dfrac{HC^2}{AF^2-È^2}-\dfrac{DE}{AE}=1\\ \)
1) Cho hcn ABCD, O thuộc dg chéo AD dg thẳng qua AO cắt cạnh AB, CD tại E,F dg thẳng qua O cắt BC,AD tại M,N cm tỉ số \(\dfrac{OE}{OP}=\dfrac{ON}{OM}\)
Trong mp xOy, cho elip (E):\(\dfrac{x^2}{25}+\dfrac{y^2}{9}=1\). Điểm M\(\varepsilon\)(E) sao cho \(F_1MF_2=90^o\). Tìm BK đg tròn nội tiếp tam giác \(MF_1F_2\)