Ôn thi vào 10
Các câu hỏi tương tự
B1 : Tìm m để (d): y = 2x + m2 + 1 song song với (d') : y = 2m2x + m2 + m
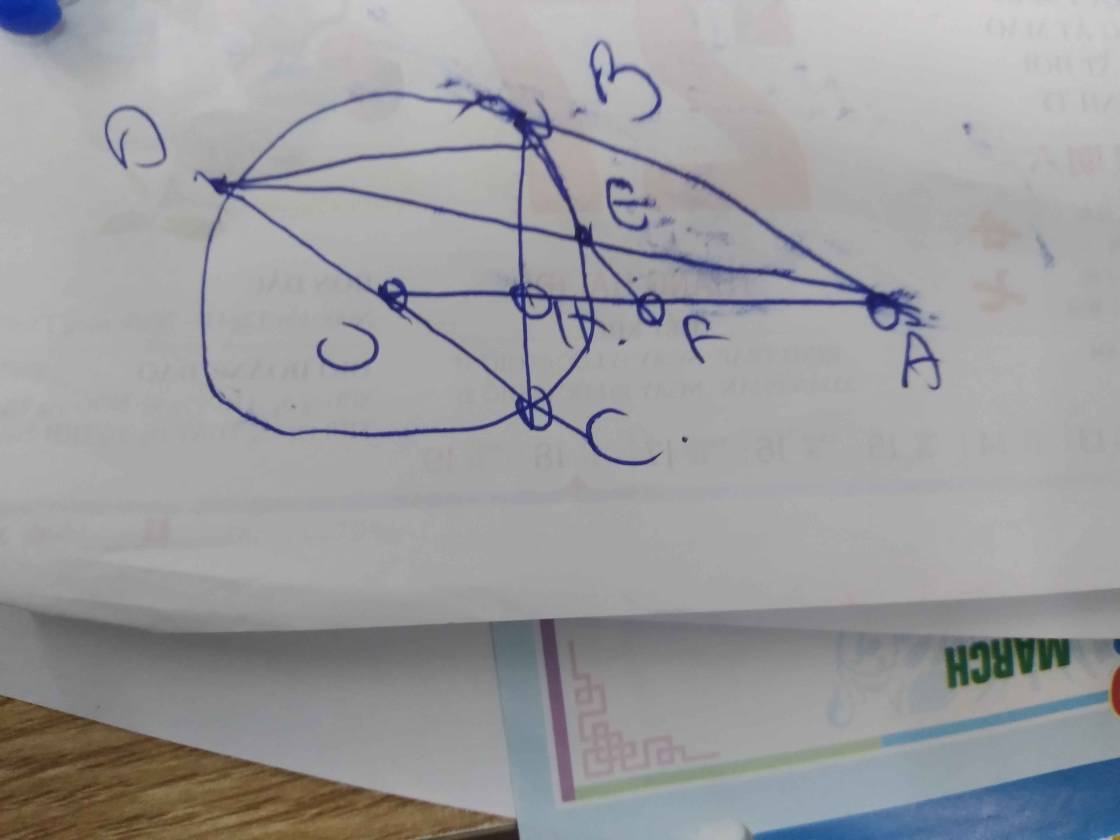
B2 : Cho (O) và A ở ngoài (O). Từ A kẻ hai tiếp tuyến AB , AC với (O) (B,C là tiếp điểm ). Đường thẳng CO cắt (O) tại điểm thứ 2 là D, AD cắt (O) tại E; BE cắt AO tại F. {H} là giao của AO với BC. Cmr :
a, ABOC nội tiếp
b, AE x AD = AH x AO
C, HE ⊥ BF
Cho (O), điểm A nằm ngoài (O) kẻ 2 tiếp tuyến AB và AC của (O) (B, C là dây). H là giao điểm của AO và BC. a) Chứng minh OA BC tại H. b) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt (O) tại E. (E ± D). Chứng minh AE . AD= AH . AO c) Qua O vẽ đường thẳng AD tại K cắt đường thẳng BC tại F. Chứng minh FD là tiếp tuyến (O) d) Gọi I là trung điểm AB. Qua I vẽ đường thẳng OA tại M. Chứng minh ND=NA
Xem chi tiết
Cho (O) qua điểm A nằm ngoài đường tròn,kẻ tiếp tuyến AB và AC với đường tròn.(BC là tiếp điểm).Kể đường kính BD,đường thẳng DC cắt BA tại E,AO cắt BC tại H,đường thẳng qua C và vuông góc với BD cắt AD tại K. Chứng minh rằng AB = AE
Cho (O) qua điểm A nằm ngoài đường tròn,kẻ tiếp tuyến AB và AC với đường tròn.(BC là tiếp điểm).Kể đường kính BD,đường thẳng DC cắt BA tại E,AO cắt BC tại H,đường thẳng qua C và vuông góc với BD cắt AD tại K. Chứng minh rằng AB = AE
Cho (O) qua điểm A nằm ngoài đường tròn,kẻ tiếp tuyến AB và AC với đường tròn.(BC là tiếp điểm).Kể đường kính BD,đường thẳng DC cắt BA tại E,AO cắt BC tại H,đường thẳng qua C và vuông góc với BD cắt AD tại K. Chứng minh rằng : a) AO vuông góc với BC b) AB = AE c) HK // BD
từ điểm A nằm ngoài đt (O) kẻ tiếp tuyến AB,AC. Đường thẳng qua cắt (O) tại D;E (D nằm giữa A và E). M là trung điểm AC, BM cắt (O) tại N (N≠B). K là tâm đtron ngoại tiếp tam giác ANC. Cm: CK vuông góc với BC.
bài cho mng tham khảo ạ
Từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC (B,C là các tiếp điểm ), đường thẳng qua A cắt đường tròn (O) tại D và E (D nằm giữa A và E, dây DE không đi qua tâm O). Gọi H là trung điẻm của DE, AE cắt BC tại Ka) Chứng minh tứ giác ABOC nội tiếp, xác định tâm đường tròn nội tiếp tứ giác ABOCb) Chứng minh HA là tia phân giác của góc BHCc) Chứng minh dfrac{2}{AK}dfrac{1}{AD}+dfrac{1}{AE}
Đọc tiếp
Từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC (B,C là các tiếp điểm ), đường thẳng qua A cắt đường tròn (O) tại D và E (D nằm giữa A và E, dây DE không đi qua tâm O). Gọi H là trung điẻm của DE, AE cắt BC tại K
a) Chứng minh tứ giác ABOC nội tiếp, xác định tâm đường tròn nội tiếp tứ giác ABOC
b) Chứng minh HA là tia phân giác của góc BHC
c) Chứng minh \(\dfrac{2}{AK}\)=\(\dfrac{1}{AD}\)+\(\dfrac{1}{AE}\)
từ một điểm A nằm ngoài đường tròn (O;R), kẻ 2 tiếp tuyến AB, AC với (O;R)(B và C là tiếp điểm). Vẽ đường kính BD a) chứng minh AO vuông góc BC tại H và CD song song OA b)AD cắt đường tròn tại K. chứng minh AD.AK=AH.AO
Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (O) ( B và C là các tiếp điểm). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai là D) ; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E .a) Chứng minh tứ giác ABOC nội tiếp đường tròn.b) Gọi H là giao điểm của A0 và BC . Chứng minh AE.AD AH.AO AB^2.c) Đường thẳng BE cắt AO tại F. Chứng minh HE vuông góc với BF.giúp tớ với ạ tớ đang cần luôn phần b và c. tớ cảm ơn nhiều ạ
Đọc tiếp
Cho đường tròn (O) và điểm A nằm ngoài đường tròn (O). Từ A kẻ hai tiếp tuyến AB, AC với đường tròn (O) ( B và C là các tiếp điểm). Đường thẳng CO cắt đường tròn (O) tại điểm thứ hai là D) ; đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là E .
a) Chứng minh tứ giác ABOC nội tiếp đường tròn.
b) Gọi H là giao điểm của A0 và BC . Chứng minh AE.AD = AH.AO = AB^2.
c) Đường thẳng BE cắt AO tại F. Chứng minh HE vuông góc với BF.
giúp tớ với ạ tớ đang cần luôn phần b và c. tớ cảm ơn nhiều ạ