đặt nhân tử chung ạ

Những câu hỏi liên quan
đặt nhân tử chung ạ
Đọc tiếp
đặt nhân tử chung ạ
\(=\left(x^2+y^2-5\right)^2-\left[2\left(xy+2\right)\right]^2\\ =\left(x^2+y^2-5-2xy-4\right)\left(x^2+y^2-5+2xy+4\right)\\ =\left[\left(x-y\right)^2-9\right]\left[\left(x+y\right)^2-1\right]\\ =\left(x-y-3\right)\left(x-y+3\right)\left(x+y-1\right)\left(x+y+1\right)\)
Đúng 2
Bình luận (0)
\(\left(x^2+y^2-5\right)^2-4\left(x^2y^2+4xy+4\right)\)
\(=\left(x^2+y^2-5\right)^2-4\left(xy+2\right)^2\)
\(=\left(x^2+y^2-5\right)^2-\left(2xy+4\right)^2=\left(x^2+y^2-5-2xy-4\right)\left(x^2+y^2-5+2xy+4\right)\)
\(=\left(x^2+y^2-2xy-9\right)\left(x^2+y^2+2xy-1\right)\)
\(=\left[\left(x-y\right)^2-9\right]\left[\left(x+y\right)^2-1\right]=\left(x-y-3\right)\left(x-y+3\right)\left(x+y-1\right)\left(x+y+1\right)\)
Đúng 2
Bình luận (0)
\(=\left(x^2+y^2-5\right)^2-4\left(xy+2\right)^2\)
\(=\left(x^2+y^2-5\right)^2-\left(2xy+4\right)^2\)
\(=\left(x^2+y^2-5-2xy-4\right)\left(x^2+y^2-5+2xy+4\right)\)
\(=\left[\left(x-y\right)^2-9\right]\left[\left(x-y\right)^2-1\right]\)
\(=\left(x-y-3\right)\left(x-y+3\right)\left(x-y-1\right)\left(x-y+1\right)\)
Đúng 2
Bình luận (0)
2x2y+xy2-xy giúp mik ạ phân tích các đa thức sau thành phân tử bằng cách đặt nhân tử chung![]()
=xy*2x+xy*y-xy*1
=xy(2x+y-1)
Đúng 0
Bình luận (0)
Tìm x
3(x-1)^2 - 3x(x-5)=1
mình đặt nhân tử chung là 3 nhưng không giả được , giải hộ mình ạ
\(3\left(x-1\right)^2-3x\left(x-5\right)=1\)
⇔ \(3\left(x^2-2x+1\right)-3x\left(x-5\right)=1\)
⇔ \(3x^2-6x+3-3x^2+15x=1\)
⇔ \(9x+3=1\)
⇔ \(9x=1-3\)
⇔ \(9x=-2\)
⇔ \(x=\dfrac{-2}{9}\)
Đúng 2
Bình luận (0)
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
6a(x+y)+3a+3bGiải hộ mik vs ạ
Bạn dặt 3 làm nhân tử chung là xong, dơn giản thui :)))))
k nha!!!!
Đúng 0
Bình luận (0)
\(6a\left(x+y\right)+3a+3b\)
\(=3\left[a\left(x+y\right)+a+b\right]\)
\(=3\left(ax+ay+a+b\right)\)
Đúng 0
Bình luận (0)
Đặt tính
a) (6x^3 - 7x^2 - x + 2) : (2x + 1)
b) (x^4 - x^3 + x^2 + 3x) : (x^2 - 2x + 3)
c) (x^2 - y^2 + 6x + 9) : (x + y + 3) ( đăth nhân tử chung)
d) (x^2 - y^2 - 4x + 4) : (x + y + 2) ( đặt nhân tử chung )
em cần gấp luôn ạ :((
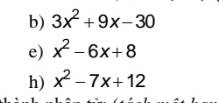
đặt nhân tử chung
h: =3(x^2+3x-10)
=3(x^2+5x-2x-10)
=3[x(x+5)-2(x+5)]
=3(x+5)(x-2)
e: =x^2-2x-4x+8
=x(x-2)-4(x-2)
=(x-2)(x-4)
h: =x^2-3x-4x+12
=x(x-3)-4(x-3)
=(x-3)(x-4)
Đúng 0
Bình luận (0)
Lời giải:
b. $3x^2+9x-30=3(x^2+3x-10)$
$=3[(x^2-2x)+(5x-10)]=3[x(x-2)+5(x-2)]=3(x-2)(x+5)$
e. $x^2-6x+8=(x^2-2x)-(4x-8)=x(x-2)-4(x-2)=(x-4)(x-2)$
h. $x^2-7x+12=(x^2-3x)-(4x-12)=x(x-3)-4(x-3)=(x-3)(x-4)$
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Xem thêm câu trả lời
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung:
-x2-4xy-4y2
= \(-\left(x^2+4xy+4y^2\right)\)
= \(-\left(x+2y\right)^2\)
Đúng 1
Bình luận (0)
Biến đa thức thành nhân tử bằng phowung pháp đặt nhân tử chung.
3xy-21x2y2
3x2y-5xy2+7xy
\(3xy-21x^2y^2=3xy\left(1-7xy\right)\)
\(3x^2y-5xy^2+7xy\)
\(=xy\left(3x-5y+7\right)\)
Đúng 1
Bình luận (0)
\(3xy-21x^2y^2\\ =3xy-3xy.7xy\\ =3xy\left(1-7xy\right)\)
Cái thứ hai không phân tích bằng đặt nhân tử chung được đâu nha=)
Đúng 0
Bình luận (0)






























