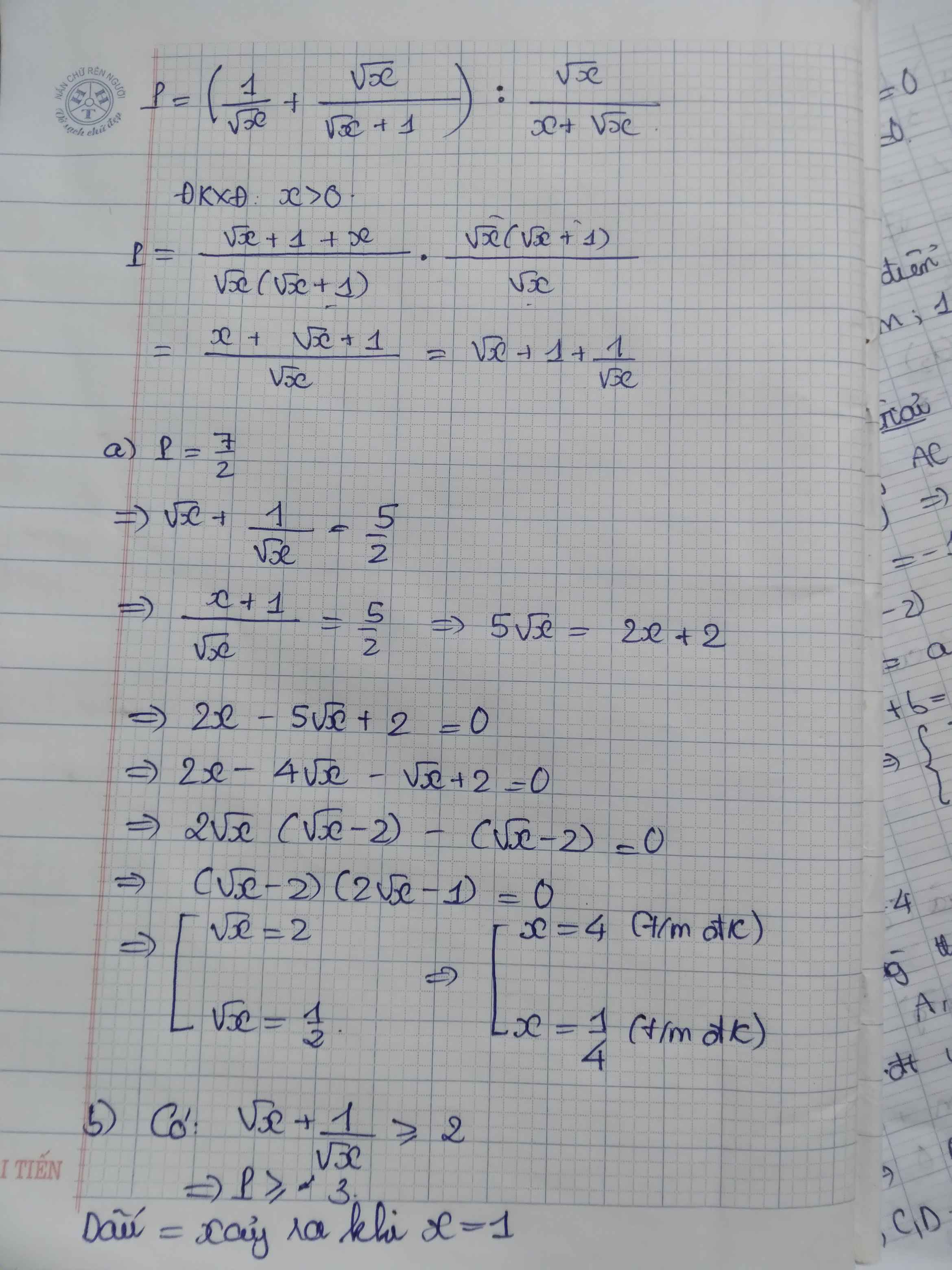ĐKXĐ: \(x\ge0;x\ne1\)

\(A=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}+\dfrac{x+2}{x\sqrt{x}-1}\)

\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{x-1-\left(x+\sqrt{x}+1\right)+x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

\(A=\dfrac{2}{7}\Rightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}+1}=\dfrac{2}{7}\)

\(\Rightarrow2\left(x+\sqrt{x}+1\right)=7\sqrt{x}\)

\(\Leftrightarrow2x-5\sqrt{x}+2=0\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{4}\end{matrix}\right.\)

\(N=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}+\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1}{x-1}\)

\(=2+\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{2x+2}{x-1}=2+\dfrac{2x+2}{\sqrt{x}}=\dfrac{2x+2\sqrt{x}+2}{\sqrt{x}}\)

N=7

=>2x+2căn x+2=7căn x

=>2x-5căn x+2=0

=>(2căn x-1)(căn x-2)=0

=>x=4 hoặc x=1/4

a) Điều kiện: \(x\ge0;x\ne1;x\ne\dfrac{1}{4}\)\(E=\left(\dfrac{2x\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt[]{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{2\sqrt{x}-1}\)

\(E=\left(\dfrac{2x\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\right).\dfrac{\sqrt{x}-1}{2\sqrt{x}-1}+\dfrac{\sqrt{x}}{2\sqrt{x}-1}\)

\(E=\dfrac{2x\sqrt{x}+x-\sqrt{x}-x\sqrt{x}-x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{2\sqrt{x}-1}+\dfrac{\sqrt{x}}{2\sqrt{x}-1}\)

\(E=\dfrac{x\sqrt{x}-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{2\sqrt{x}-1}+\dfrac{\sqrt{x}}{2\sqrt{x}-1}\)

\(E=\dfrac{x\sqrt{x}-2\sqrt{x}}{\left(x+\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{2\sqrt{x}-1}\)

\(E=\dfrac{x\sqrt{x}-2\sqrt{x}+x\sqrt{x}+x+\sqrt{x}}{\left(x+\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(E=\dfrac{2x\sqrt{x}-\sqrt{x}+x}{\left(x+\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(E=\dfrac{\sqrt{x}\left(2x+\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(E=\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}\)

b)Vì \(x\ge0\) nên \(x+\sqrt{x}\ge0\) và \(x+\sqrt{x}+1>0\)

Do đó: \(E\ge0\). Dấu "=" xảy ra \(\Leftrightarrow x=0\)

c)\(E\ge\dfrac{6}{7}\Leftrightarrow\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}\ge\dfrac{6}{7}\Leftrightarrow7x+7\sqrt{x}\ge6x+6\sqrt{x}+6\)

                \(\Leftrightarrow x+\sqrt{x}-6\ge0\Leftrightarrow x-2\sqrt{x}+3\sqrt{x}-6\ge0\)

                 \(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)\ge0\)

                  \(\Leftrightarrow\sqrt{x}-2\ge0\Leftrightarrow\sqrt{x}\ge2\Leftrightarrow x\ge4\)

1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)

\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)

\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)

Để \(P=\dfrac{7}{2}\) thì \(2x+2\sqrt{x}+2-7\sqrt{x}=0\)

\(\Leftrightarrow2x-4\sqrt{x}-\sqrt{x}+2=0\)

\(\Leftrightarrow2\sqrt{x}\left(\sqrt{x}-2\right)-\left(\sqrt{x}-2\right)=0\)

\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{4}\end{matrix}\right.\)

a)ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)

 \(\Rightarrow A=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(\Rightarrow A=\dfrac{x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(\Rightarrow A=\dfrac{x+\sqrt{x}-2\sqrt{x}+2-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(\Rightarrow A=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(\Rightarrow A=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(\Rightarrow A=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)

b) \(x=9\Rightarrow A=\dfrac{3}{3+1}=\dfrac{3}{4}\)

\(x=7-4\sqrt{3}\Rightarrow A=\dfrac{\sqrt{7-4\sqrt{3}}}{\sqrt{7-4\sqrt{3}}+1}=\dfrac{\sqrt{7-2\sqrt{12}}}{\sqrt{7-2\sqrt{12}}+1}=\dfrac{\sqrt{4-2\sqrt{3}\sqrt{4}+3}}{\sqrt{4-2\sqrt{3}\sqrt{4}+3}+1}=\dfrac{2-\sqrt{3}}{2-\sqrt{3}+1}=\dfrac{2-\sqrt{3}}{3-\sqrt{3}}=\dfrac{\left(2-\sqrt{3}\right)\left(3+\sqrt{3}\right)}{\left(3-\sqrt{3}\right)\left(3+\sqrt{3}\right)}=\dfrac{3-\sqrt{3}}{6}\)

a: \(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{x-9}\cdot\dfrac{\sqrt{x}-7+\sqrt{x}+1}{\sqrt{x}+1}\)

\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{x-9}\cdot\dfrac{2\sqrt{x}-6}{\sqrt{x}+1}\)

\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+1}\cdot\dfrac{2}{\sqrt{x}+3}=-\dfrac{6}{\sqrt{x}+3}\)

b: P>=-1/2

=>P+1/2>=0

=>\(\dfrac{-6}{\sqrt{x}+3}+\dfrac{1}{2}>=0\)

=>\(\dfrac{-12+\sqrt{x}+3}{2\left(\sqrt{x}+3\right)}>=0\)

=>căn x-9>=0

=>x>=81

c: căn x+3>=3

=>6/căn x+3<=6/3=2

=>-6/căn x+3>=-2

Dấu = xảy ra khi x=0

\(a,\) Rút gọn 

\(A=\dfrac{3}{\sqrt{7}-2}+\sqrt{\left(\sqrt{7}-3\right)^2}\)

\(=\dfrac{3}{\sqrt{7}-2}+\left|\sqrt{7}-3\right|\)

\(=\dfrac{3}{\sqrt{7}-2}+3-\sqrt{7}\)

\(=\dfrac{3+\left(3-\sqrt{7}\right)\left(\sqrt{7}-2\right)}{\sqrt{7}-2}\)

\(=\dfrac{3+3\sqrt{7}-6-7+2\sqrt{7}}{\sqrt{7}-2}\)

\(=\dfrac{5\sqrt{7}-10}{\sqrt{7}-2}\)

\(=\dfrac{5\left(\sqrt{7}-2\right)}{\sqrt{7}-2}\)

\(=5\)

Vậy \(A=5\)

\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{x-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{x-1}\left(dkxd:x\ge0,x\ne1\right)\)

\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right).\left(\dfrac{x-1}{\sqrt{x}+1}\right)\)

\(=\dfrac{\sqrt{x}.\sqrt{x}-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)

\(=\dfrac{x-\sqrt{x}}{x-\sqrt{x}}.\left(\sqrt{x}-1\right)\)

\(=\sqrt{x}-1\)

Vậy \(B=\sqrt{x}-1\)

\(b,\) Để \(B< A\) thì \(\sqrt{x}-1< 5\)

\(\Leftrightarrow\sqrt{x}< 6\)

\(\Leftrightarrow x< 36\)

8: Để \(P< \dfrac{1}{4}\) thì \(P-\dfrac{1}{4}< 0\)

\(\Leftrightarrow\dfrac{4\sqrt{x}-8-\sqrt{x}-1}{\sqrt{x}+1}< 0\)

\(\Leftrightarrow3\sqrt{x}< 9\)

hay x<9

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne1\end{matrix}\right.\)

7.

\(P< 1\Leftrightarrow\dfrac{x+\sqrt{x}}{\sqrt{x}-1}< 1\)

\(\Leftrightarrow\dfrac{x+\sqrt{x}}{\sqrt{x}-1}-1< 0\)

\(\Leftrightarrow\dfrac{x+\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\dfrac{x+1}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\sqrt{x}-1< 0\)

\(\Leftrightarrow x< 1\)

Vậy \(0\le x< 1\)

8.

\(P< \dfrac{1}{4}\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< \dfrac{1}{4}\)

\(\Leftrightarrow4\left(\sqrt{x}-2\right)< \sqrt{x}+1\)

\(\Leftrightarrow4\sqrt{x}-8< \sqrt{x}+1\)

\(\Leftrightarrow3\sqrt{x}< 9\)

\(\Leftrightarrow x< 9\)

Vậy \(0\le x< 9;x\ne1\)

a) \(A=\sqrt{28}-\sqrt{63}+\dfrac{7+\sqrt{7}}{\sqrt{7}}-\sqrt{\left(\sqrt{7}+1\right)^2}\)

\(=2\sqrt{7}-3\sqrt{7}+\dfrac{\sqrt{7}\left(\sqrt{7}+1\right)}{\sqrt{7}}-\left|\sqrt{7}+1\right|\)

\(=-\sqrt{7}+\sqrt{7}+1-\sqrt{7}-1=-\sqrt{7}\)

\(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\dfrac{4\sqrt{x}+12}{\sqrt{x}}\)

\(=\dfrac{\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}\)

\(=\dfrac{8}{\sqrt{x}-3}\)

b) \(A>B\Rightarrow-\sqrt{7}>\dfrac{8}{\sqrt{x}-3}\Rightarrow\dfrac{8}{\sqrt{x}-3}+\sqrt{7}< 0\)

\(\Rightarrow\dfrac{\sqrt{7x}+8-3\sqrt{7}}{\sqrt{x}-3}< 0\)

Ta có: \(\left\{{}\begin{matrix}8=\sqrt{64}\\3\sqrt{7}=\sqrt{63}\end{matrix}\right.\Rightarrow8-3\sqrt{7}>0\Rightarrow8-3\sqrt{7}+\sqrt{7x}>0\)

\(\Rightarrow\sqrt{x}-3< 0\Rightarrow\sqrt{x}< 3\Rightarrow x< 9\Rightarrow0< x< 9\)