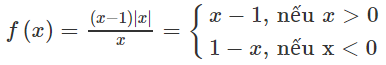Vẽ đồ thị của hàm số \(y=\dfrac{\left|x\right|}{x}\)

Những câu hỏi liên quan
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
vẽ đồ thị của hàm số sau
a) \(y=3^x\)
b) \(y=\left(\dfrac{1}{2}\right)^x\)
a: Bảng giá trị:
| x | 1 | 2 | 3 |
| \(y=3^x\) | 3 | 9 | 27 |
Vẽ đồ thị:
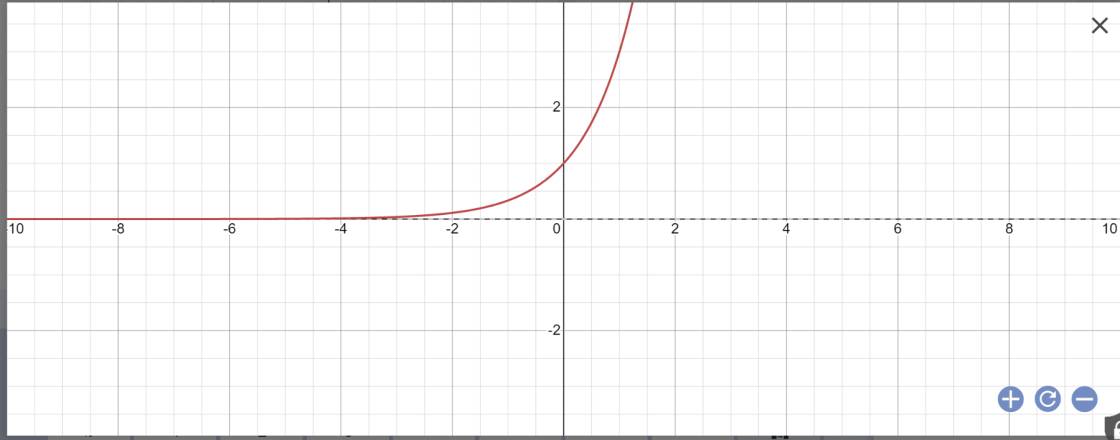
b: Bảng giá trị:
| x | 2 | 3 | 4 |
| \(y=\left(\dfrac{1}{2}\right)^x\) | 1/4 | 1/8 | 1/16 |
vẽ đồ thị:
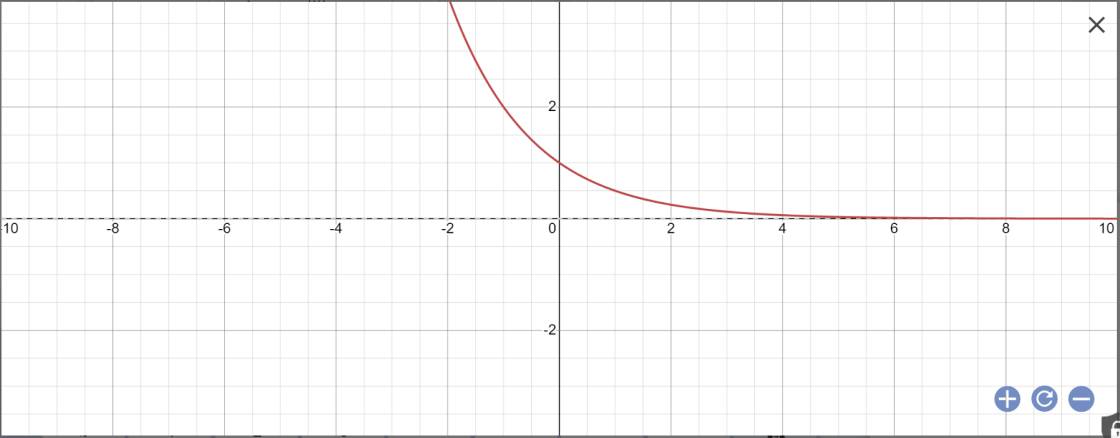
Đúng 1
Bình luận (0)
Cho hàm số \(y=-\dfrac{5}{2}x\)
a) Xác định vị trí của điểm \(A\left(1,-\dfrac{5}{2}\right)\) trên mặt phẳng tọa độ , và vẽ đồ thị hàm số đó.
b) Xét xem trong các điểm sau , điểm nào thuộc đồ thị hàm số ? \(B\left(2,-5\right),C\left(3,7\right),D\left(l,\dfrac{5}{2}\right),E\left(0,4\right)\)
a: Thay x=1 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)
Vậy: \(A\left(1;-\dfrac{5}{2}\right)\) thuộc đồ thị hàm số y=-5/2x
b: Thay x=2 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot2=-5\)
=>B(2;-5) thuộc đồ thị hàm số y=-5/2x
Thay x=3 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot3=-\dfrac{15}{2}\)<>7
=>\(C\left(3;7\right)\) không thuộc đồ thị hàm số y=-5/2x
Thay x=1 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)<>5/2
=>\(D\left(1;\dfrac{5}{2}\right)\) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)
Thay x=0 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot0=0\)<>4
=>E(0;4) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)
Đúng 1
Bình luận (0)
bài1a) hãy xác định hàm số yax^2 bt rằng đồ thị của nó đi qua điểm M(-2;2) b) vẽ đồ thị hàm số y dfrac{1}{2}x^2bài 2 a)left{{}begin{matrix}4x+5y3x-3y5end{matrix}right. b) left{{}begin{matrix}dfrac{1}{x}+dfrac{1}{y}dfrac{4}{5}dfrac{1}{x}-dfrac{1}{y}dfrac{1}{5}end{matrix}right. giải hộ tui với
Đọc tiếp
bài1
a) hãy xác định hàm số y=ax\(^2\) bt rằng đồ thị của nó đi qua điểm \(M(-2;2)\)
b\()\) vẽ đồ thị hàm số y= \(\dfrac{1}{2}x^2\)
bài 2
a)\(\left\{{}\begin{matrix}4x+5y=3\\x-3y=5\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{4}{5}\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\)
giải hộ tui với ![]()
Bài 1:
a: Thay x=-2 và y=2 vào hàm số, ta được:
4a=2
hay a=1/2
Bài 2:
a: \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\3y=x-5=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(2;\dfrac{10}{3}\right)\)
Đúng 2
Bình luận (0)
Cho hàm số ymx+3 có đồ thị là left(d_1right) và hàm số ydfrac{-1}{m}x+3left(mne0right) có đồ thị là left(d_2right)
1) Với m 1
a) Vẽ đồ thị left(d_1right) và left(d_2right) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của left(d_1right) và left(d_2right).
Đọc tiếp
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị là \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
Với m = 1
(d1) có dạng y = x + 3
(d2) có dạng y = -x + 3
Phương trình hoành độ giao điểm
-x + 3 = x + 3
<=> x = 0
Với x = 0 <=> y = 3
Tọa độ giao điểm A(0;3)
Đúng 1
Bình luận (0)
Cho hàm số ymx+3 có đồ thị là left(d_1right) và hàm số ydfrac{-1}{m}x+3left(mne0right) có đồ thị left(d_2right)1) Với m 1 a) Vẽ đồ thị left(d_1right) và left(d_2right) trên cùng một mặt phẳng tọa độ b) Tìm tọa độ giao điểm của left(d_1right) và left(d_2right).
Đọc tiếp
Cho hàm số \(y=mx+3\) có đồ thị là \(\left(d_1\right)\) và hàm số \(y=\dfrac{-1}{m}x+3\left(m\ne0\right)\) có đồ thị \(\left(d_2\right)\)
1) Với m = 1
a) Vẽ đồ thị \(\left(d_1\right)\) và \(\left(d_2\right)\) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\).
1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3
a: 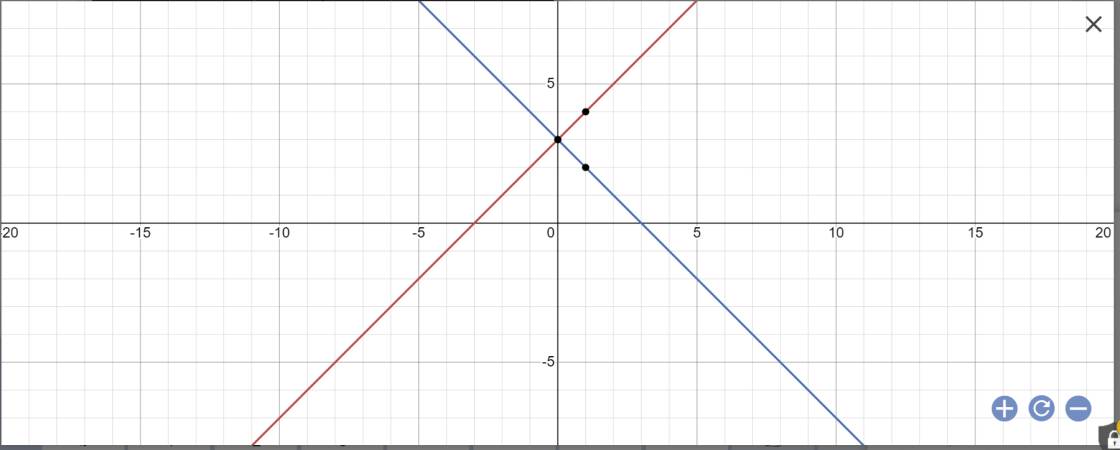
b: Tọa độ giao điểm là:
x+3=-x+3 và y=x+3
=>x=0 và y=3
Đúng 2
Bình luận (0)
cho hàm số: \(y=\left(2m-1\right)x+n\) với \(\left(m\ne\dfrac{1}{2}\right)\)
Tìm giá trị của m, n biết n=2m và đồ thị hàm số \(y=\left(2m-1\right)x+n\) cắt đồ thị hàm số \(y=\dfrac{1}{2}x-4\) tại một điểm trên trục tung
Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2
Đúng 0
Bình luận (0)
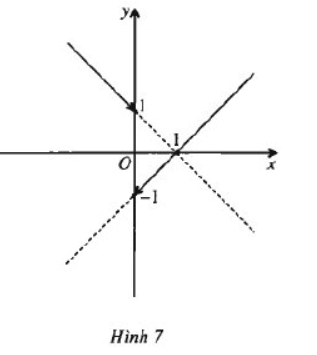
Cho hàm số \(f\left(x\right)=\dfrac{\left(x-1\right)\left|x\right|}{x}\)
Vẽ đồ thị của hàm số này. Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó ?
Hàm số này có tập xác định là R \ {0}

Đúng 0
Bình luận (0)
c2a/ ko sử dụng mt cầm tay, giải hptleft{{}begin{matrix}x+2y43x-y5end{matrix}right.b/ cho hàm số y-dfrac{1}{2}x^2có đồ thị (P)- vẽ đồ thị (P) của hàm số- cho đường thẳng ymx+nleft(Deltaright). tìm m.n để đường thẳng (Delta) song song vs đường thẳng y-2x+5left(dright) và có duy nhất 1 điểm chung vs đồ thị (P)
Đọc tiếp
c2
a/ ko sử dụng mt cầm tay, giải hpt
\(\left\{{}\begin{matrix}x+2y=4\\3x-y=5\end{matrix}\right.\)
b/ cho hàm số \(y=-\dfrac{1}{2}x^2\)có đồ thị (P)
- vẽ đồ thị (P) của hàm số
- cho đường thẳng \(y=mx+n\left(\Delta\right)\). tìm m.n để đường thẳng (\(\Delta\)) song song vs đường thẳng \(y=-2x+5\left(d\right)\) và có duy nhất 1 điểm chung vs đồ thị (P)
b: Vì (Δ)//(d) nên m=-2
Vậy: (Δ): y=-2x+n
Phương trình hoành độ giao điểm là
\(-\dfrac{1}{2}x^2+x-n=0\)
\(\text{Δ}=1^2-4\cdot\dfrac{-1}{2}\cdot\left(-n\right)=1-2n\)
Để (d) tiếp xúc với (P) thì -2n+1=0
hay n=1/2
Đúng 0
Bình luận (0)
Tịnh tiến đồ thị hàm số y= cos x sang phải \(\dfrac{\pi}{2}\) ta được đồ thị hàm số nào
A. \(y=sinx\)
B.\(y=-cosx\)
C.\(y=\)\(cos\left(x+\dfrac{\pi}{2}\right)\)
D.\(y=sin\left(x-\dfrac{\pi}{2}\right)\)