Hàm số này có tập xác định là R \ {0}

Hàm số này có tập xác định là R \ {0}


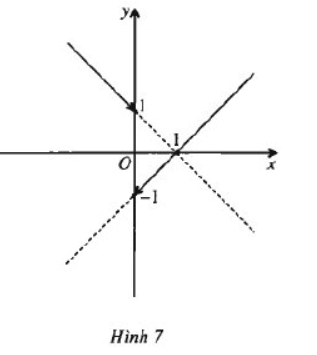
Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}3x+2;\left(x< -1\right)\\x^2-1;\left(x\ge-1\right)\end{matrix}\right.\)
a) Vẽ đồ thị hàm số \(y=f\left(x\right)\). Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó ?
b) Khẳng định nhận xét trên bằng một chứng minh ?
Cho hàm số \(f\left(x\right)=\dfrac{x+1}{x^2+x-6}\) và \(g\left(x\right)=\tan x+\sin x\)
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục ?
tìm các khoảng và nửa khoảng mà trên đó mỗi hàm số liên tục:
f(x)=\(\left\{{}\begin{matrix}2x+1\left(0< x< 2\right)\\2\left(x\ge2\right)\\\left(x-1\right)^2\left(x\le0\right)\end{matrix}\right.\)
f(x)=\(\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{x-1}\left(x\ne1\right)\\\dfrac{-1}{2}\left(x=1\right)\end{matrix}\right.\)
Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng (a; b) chứa điểm \(x_0\)
Chứng minh rằng nếu \(\lim\limits_{x\rightarrow x_0}\dfrac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=L\) thì hàm số \(f\left(x\right)\) liên tục tại điểm \(x_0\) ?
Tìm a để hàm số liên tục trên R
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{\left|x-2\right|},x\ne2\\a,x=2\end{matrix}\right.\)
tìm m để hàm số
\(f\left(x\right)\left\{{}\begin{matrix}\dfrac{\sqrt[3]{3x+5}-2}{1-x^3},x< 1\\\dfrac{2m\sqrt{x}+3}{5},x>=1\end{matrix}\right.\)liên tục trên r
Tìm giá trị của tham số m để hàm số \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{x}-1}{x^2-1};\left(x\ne1\right)\\m^2;\left(x=1\right)\end{matrix}\right.\) liên tục trên \(\left(0;+\infty\right)\) ?
1/ Xét tính liên tục của hàm số tại một điểm:
a) \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-4}{x^2+x-2},x\ne2\\2x+1,x=2\end{matrix}\right.\left(x_0=2\right)}\)
Xác định tính liên tục của hàm số trên R\(f\left(x\right)=\left\{{}\begin{matrix}2x^2-3khi\left|x\right|< 2\\5khi\left|x\right|=2\\3x-1khi\left|x\right|>2\end{matrix}\right.\)