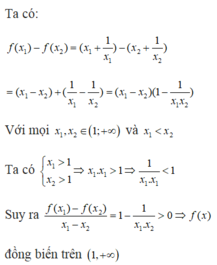1 nghịch biến(a<0) 

2 đồng biến

3,4 thay các g trị tm đk vào

hojk tốt

a) Đk:\(x\in R\)

TH1:Xét \(x\in\left(3;+\infty\right)\)

Lấy \(x_1;x_2\in\left(3;+\infty\right)\) thỏa mãn \(x_1\ne x_2\)

Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{2x_1^2-4x_1+3-\left(2x_2^2-4x_2+3\right)}{x_1-x_2}\)\(=2\left(x_1+x_2\right)-4\)

Do \(x_1;x_2\in\left(3;+\infty\right)\)\(\Rightarrow2\left(x_1+x_2\right)>12\Leftrightarrow2\left(x_1+x_2\right)-4>8>0\)

\(\Rightarrow I>0\)

Hàm đồng biến trên \(\left(3;+\infty\right)\)

TH2:Xét \(x\in\left(-10;1\right)\)

Lấy \(x_1;x_2\in\left(-10;1\right):x_1\ne x_2\)

Xét \(I=2\left(x_1+x_2\right)-4\)

Do \(x_1< 1;x_2< 1\Rightarrow2\left(x_1+x_2\right)< 4\Rightarrow I=2\left(x_1+x_2\right)-4< 0\)

Hàm nb trên khoảng \(\left(-10;1\right)\)

b)Làm tương tự,hàm nb trên \(\left(1;+\infty\right)\) và đb trên \(\left(-10;-2\right)\)

c)Đk: \(x\in R\backslash\left\{2\right\}\)

=>Hàm số xác định trên \(\left(-\infty;2\right)\)

Lấy \(x_1;x_2\in\left(-\infty;2\right):x_1\ne x_2\)

Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{x_1}{x_1-2}-\dfrac{x_2}{x_2-2}}{x_1-x_2}=\dfrac{-2}{\left(x_1-2\right)\left(x_2-2\right)}\)

Do \(x_1;x_2< 2\Rightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)

\(\Rightarrow I=-\dfrac{2}{\left(x_1-2\right)\left(x_2-2\right)}< 0\)

Hàm nb trên ​\(\left(-\infty;2\right)\)​

d)\(I=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)

Hàm đb trên \(\left(-1;+\infty\right)\) ; \(\left(-3;-2\right)\)

e)TXĐ:D=R

Lấy \(x_1;x_2\in\left(0;+\infty\right):x_1< x_2\)

​​\(T=f\left(x_1\right)-f\left(x_2\right)=x_1^{2020}+x_1^2-3-x_2^{2020}-x_2^2+3=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2\)

Do \(x_1< x_2\Rightarrow x_1^{2020}< x_2^{2020};x_1^2< x_2^2\)

​\(\Rightarrow T=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2< 0\)​

Hàm đb trên \(\left(0;+\infty\right)\)

a: TXĐ: D=R

Khi \(x\in D\Rightarrow-x\in D\)

\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)

\(=-x^2+2x+3\)

\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)

Vậy: Hàm số không chẵn không lẻ

Áp dụng bất đẳng thức AM - GM ta có:

\(f\left(x\right)=x+\left(2x+\dfrac{1}{2x}\right)\ge1+2\sqrt{2x.\dfrac{1}{2x}}=3\).

Dấu "=" xảy ra khi và chỉ khi x = 1.

Vậy...

a)

\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)

\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)

Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).

\( \Rightarrow {x_1} - {x_2} < 0\)

\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)

Ta có:

\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)

=> Hàm số nghịch biến trên (-2;-1)

Vậy hàm số giảm khi x tăng từ -2 đến -1

b)

\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)

Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).

\( \Rightarrow {x_1} - {x_2} < 0\)

\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)

Ta có:

\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)

=> Hàm số đồng biến trên (1;2)

Vậy hàm số tăng khi x tăng từ 1 đến 2.

\(y'=\dfrac{2x^2-4mx-m^2+2m-1}{\left(x-m\right)^2}\)

Hàm đồng biến trên khoảng đã cho khi với mọi \(x>1\) ta có:

\(\left\{{}\begin{matrix}2x^2-4mx-m^2+2m-1\ge0\left(1\right)\\m\le1\end{matrix}\right.\)

Xét (1): ta có \(\Delta'=4m^2-2\left(-m^2+2m-1\right)=6m^2-4m+2>0\) ; \(\forall m\)

\(\Rightarrow\) (1) thỏa mãn khi: \(x_1< x_2\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)\ge0\\\dfrac{x_1+x_2}{2}< 1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_2\right)+1\ge0\\x_1+x_2< 2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-m^2+2m-1}{2}-2m+1\ge0\\2m< 2\end{matrix}\right.\) \(\Rightarrow-1-\sqrt{2}\le m\le-1+\sqrt{2}\)

Đáp án A