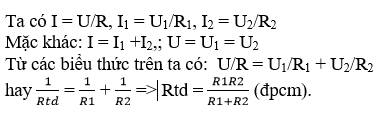CMR: \(\dfrac{1}{R_{tđ_{ }}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\)

Những câu hỏi liên quan
Hãy chứng minh công thức tính điện trở tương đương của đoạn mạch gồm hai điện trở R2, R3 mắc song song là: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\)
Trong mạch gồm hai điện trở R2, R3 mắc song song, cường độ dòng điện chạy qua các điện trở là: \(I_1=\dfrac{U_1}{R_1}\) và \(I_2=\dfrac{U_2}{R_2}\), trong đó U1 = U2.
Cường độ dòng điện chạy qua đoạn mạch là I = I1 + I2 = \(\dfrac{U}{R_1}+\dfrac{U}{R_2}\) = \(\dfrac{U}{R_{td}}\). Từ đó ta có \(\dfrac{1}{R_{td}}\) = \(\dfrac{1}{R_1}+\dfrac{1}{R_2}\)
Suy ra: \(R_{td}=\dfrac{R_1R_2}{R_1+R_2}\)
Đúng 0
Bình luận (0)
CMR: Rtđ=\(\dfrac{R_1.R_2}{R_1+R_2}\)
Ta có
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}=\dfrac{R_2}{R_1.R_2}+\dfrac{R_1}{R_1.R_2}=\dfrac{R_1+R_2}{R_1.R_2}\\ \Rightarrow\dfrac{1}{R_{tđ}}=\dfrac{R_1+R_2}{R_1.R_2}\\ \Rightarrow R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, M là trung điểm BC, biết BC = a. Gọi r, r1, r2 theo thứ tự là bán kính đường tròn nội tiếp các tam giác ABC, ABM, ACM.
CMR : \(\dfrac{1}{r_1}+\dfrac{1}{r_2}\ge2\left(\dfrac{1}{r}+\dfrac{2}{a}\right)\)
Chứng minh công thức: \(\dfrac{R_1}{R_2}=\dfrac{l_1}{l_2}.\dfrac{S_2}{S_1}\)
Mọi người giúp em với!!!!!!!!!!
đề này bạn thiếu nhưng do mình đọc cái chủ đề nên:
công thức \(\dfrac{R_1}{R_2}=\dfrac{l_1}{l_2}.\dfrac{S_2}{S_1}\) tồn tại khi có chung Điện trở suất là ρ\
Ta có: \(R_1=\rho\dfrac{l_1}{S_1}\)(1)
\(R_2=\rho\dfrac{l_2}{S_2}\)(2)
Lập tỉ số \(\dfrac{\left(1\right)}{\left(2\right)}\) Ta được: \(\dfrac{R_1}{R_2}=\dfrac{\rho.\dfrac{l_1}{S_1}}{\rho.\dfrac{l_2}{S_2}}=\dfrac{\dfrac{l_1}{S_1}}{\dfrac{l_2}{S_2}}=\dfrac{l_1}{S_1}.\dfrac{S_2}{l_2}=\dfrac{l_1}{l_2}.\dfrac{S_2}{S_1}\)
Đúng 0
Bình luận (0)
I1=\(\dfrac{R_2}{R_1+R_2}\times I_{12}\)
cm giúp mình vs cố gáng nhanh nhanh giúp mình
Vì R1//R2 nên
U=U1=U2
Mà U=Rtđ*I=\(\frac{R1\cdot R2}{R1+R2}\cdot I12\)
⇒U1=U2=\(\frac{R1\cdot R2}{R1+R2}\cdot I12\)
Ta có I1=\(\frac{U1}{R1}=\frac{\frac{R1\cdot R2}{R1+R2}\cdot I12}{R1}=\frac{\frac{R1\cdot R2}{R1+R2}}{R1}\cdot I12=\frac{R2}{R1+R2}\cdot I12\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Cho 2 đường tròn (O_1,R_1) và (O_2,R_2) tiếp tuyến tại A .Hai điểm B,C di chuyển trên (O_1) và (O_2) sao cho góc BAC90^0.Vẽ AH perpBC tại H .Chứng minh AH ledfrac{2R_1.R_2}{R_1+R_2}
Đọc tiếp
Cho 2 đường tròn (\(O_1\),\(R_1\)) và (\(O_2\),\(R_2\)) tiếp tuyến tại A .Hai điểm B,C di chuyển trên (\(O_1\)) và (\(O_2\)) sao cho góc BAC=\(90^0\).Vẽ AH \(\perp\)BC tại H .Chứng minh AH \(\le\)\(\dfrac{2R_1.R_2}{R_1+R_2}\)
Thứ nhất: $(O_1); (O_2)$ tiếp xúc nhau tại $A$ chứ không phải tiếp tuyến tại $A$.
Thứ hai: $(O_1)$ và $(O_2)$ tiếp xúc trong, tiếp xúc ngoài hay đề chỉ nói chung chung là tiếp xúc thôi hả bạn?
Đúng 0
Bình luận (1)
tính tỉ số \(\dfrac{S_2}{S_1}=\dfrac{d^2_2}{d^2_1}\) và so sánh vơi tỉ số \(\dfrac{R_1}{R_2}\)
Hãy chứng minh rằng điện trở tương đương \(R_{tđ}\) của một đoạn mạch song song ,chẳng hạn gồm ba điện trở \(R_1,R_2,R_3\) mắc song song với nhau, thì nhỏ hơn mỗi điện trở thành phần (\(R_{tđ}< R_1;R_{tđ}< R_2;R_{tđ}< R_3\))
Xét đoạn mạch gồm ba điện trở \(R_1,R_2,R_3\) mắc song song :
Ta có : \(I=I_1+I_2+I_3\)
\(U=U_1=U_2=U_3\) hay \(IR_{tđ}=I_1R_1=I_2R_2=I_3R_3\)
Vì \(I_1< I\), do đó \(R_{tđ}< R_1\).
Do \(I_2< I\) nên \(R_{tđ}< R_2\), tương tự với \(I_3< I\Rightarrow R_{tđ}< R_3\). (đpcm)
Đúng 0
Bình luận (0)
Cách khác cách của Minh :v
Trong đoạn mạch song song mắc n điện trở:
\(\dfrac{1}{R_{rđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}+...+\dfrac{1}{R_n}\)
Ta có: \(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_1}\Rightarrow R_{tđ}< R_1\)
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_2}\Rightarrow R_{tđ}< R_2\)
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_3}\Rightarrow R_{tđ}< R_3\)
...
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_n}\Rightarrow R_{tđ}< R_n\)
Do đó điện trở tương đương của đoạn mạch song song nhỏ hơn điện trở mỗi thành phần.
Đúng 0
Bình luận (0)
Cho 3 điện trở \(R_1,R_2,R_3.\) Hỏi có bao nhiêu cách mắc điện trở này thành mạch điện. Với mỗi mạch điện tính \(R_{tươngđương}\) ; với \(R_1=2ôm\) ,\(R_2=4ôm,\) \(R_3=6ôm\)