Cho hình vuông ABCD có cạnh bằng a.Đường thẳng qua đỉnh C cắt AB và AD kéo dài tại F và E.
a.Chứng minh rằng :DE.BF không đổi
b. Chứng minh :\(\dfrac{DE}{BF}=\dfrac{AE^2}{ÀF^2}\)
Qua đỉnh A của hình vuông ABCD cạnh bằng a, vẽ đường thẳng cắt BC ở E và cắt đường thẳng DC ở F. Chứng minh: \(\dfrac{1}{AE^{2^{ }}}+\dfrac{1}{ÀF^2}=\dfrac{1}{a^2}\)
help me
Cho hình thang ABCD (AB //CD)
Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự tại E và F
Chứng minh rằng :
a) \(\dfrac{AE}{ED}=\dfrac{BF}{FC}\)
b) \(\dfrac{AE}{AD}=\dfrac{BF}{BC}\)
c) \(\dfrac{DE}{DA}=\dfrac{CF}{CB}\)
Giải:
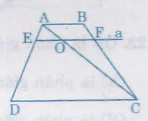
a) Nối AC cắt EF tại O
∆ADC có EO // DC => = (1)
∆ABC có OF // AB => = (2)
Từ 1 và 2 => =
b) Từ = => =
hay =
c) Từ = => =
=>
CHO HÌNH VUÔNG ABCD CÓ ĐỘ DÀI CẠNH LÀ a. MỘT ĐG THẲNG d QUA ĐỈNH C CẮT TIA AB Ở E, CẮT TIA AD Ở F
A) CM \(BE\cdot DF=a^2\) VÀ \(BE:DF=AE^2:AF^2\)
B) CM KHI d QUAY QUANH C SAO CHO TỒN TẠI CÁC ĐIỂM E VÀ F THÌ \(\dfrac{1}{AE}+\dfrac{1}{AF}\) KHÔNG THAY ĐỔI GIÁ TRỊ
Cho hình vuông ABCD. Lấy điểm E trên cạnh BC. Tia AE cắt đường thẳng CD tại G. Trên mặt phẳng bờ là đg thẳng AE chứa tia AD, kẻ AF vuông góc AE và AF= AE.
b. chứng minh \(\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AG^2} \)
a. chứng minh F, D, C thẳng hàng
c. Biết AD= 13cm, AF : AG= 1:3. Tính độ dài của FG
Cho tam giác ABC và G là trọng tâm của nó. Một đường thẳng d đi qua trọng tâm G cắt cạnh AB tại D, cắt cạnh AC tại E.
a) chứng minh rằng khi đường thẳng d thay đổi tổng AB/AD + AC/AE luôn không đổi
b) gọi E,F,P lần lượt là hình chiếu của B,C trên đường thẳng DE. Chứng minh rằng BF+CP=AH.
c) xác định vị trí của đường thẳng d để tổng diện tích hai tam giác BDE và CDE bé nhất.
cho đt (O) và A nằm ngoài đt. Từ A kẻ tiếp tuyến AB,AC (B,C là tiếp điểm). Đường thẳng CO cắt (O) tại D (D≠C). AD cắt (O) tại E (E≠A). BE cắt AO tại F, AO cắt BC tại H.
Chứng minh HE vuông góc BF. Và \(\dfrac{HC^2}{AF^2-È^2}-\dfrac{DE}{AE}=1\\ \)
Cho hình vuông ABCD , một điểm E bất kỳ trên cạnh BC . Tia Ax AE cắt cạnh CD
kéo dài tại F . Kẻ trung tuyến AI của tam giác AEF và kéo dài cắt cạnh CD tại K .
Đường thẳng qua E và song song với AB cắt AI tại G .
a) Tam giác AEF là tam giác gì?
b) Tứ giác EGFK là hình gì?
c) Chứng minh B I D , , thẳng hàng.
d) Cho AB a , tính chu vi tam giác ECK .
e) Chứng minh diện tích 1 2
2
S a AKE .
f) Dựng hình bình hành AEPF , chứng minh đỉnh P luôn chạy trên một đoạn
thẳng cố định.
Cho tam giác ABC vuông ở B, trên cạnh AC lấy điểm E sao cho AE = AB. Tia phân giác của góc A cắt BC tại D.
a, Chứng minh Δ ADB = ΔADE
b, Chứng minh DE\(\perp\)AC
c, Một đường thẳng qua C và vuông góc với AD cắt đường thẳng AB ở F. Chứng minh BF=CE
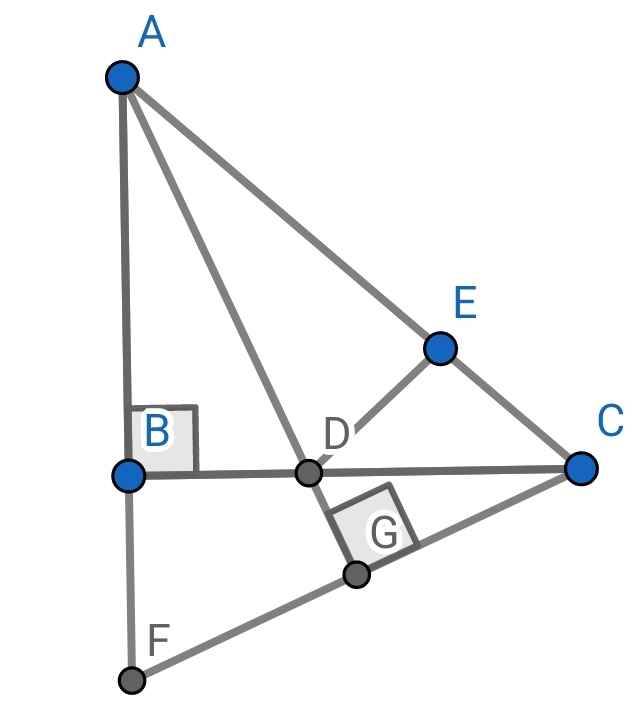
a) Xét ∆ADB và ∆ADE có:
AD chung
Góc BAD = góc EAD (AD là tia phân giác của góc BAC)
AB = AE (gt)
⇒∆ADB = ∆ADE (c-g-c)
b) Do ∆ADB = ∆ADE (c-g-c)
⇒góc ABD = góc AED (hai góc tương ứng)
⇒góc AED = 90⁰
Hay DE vuông góc AC
c) Gọi G là giao điểm của CF và AD
Do góc BAD = góc EAD (cmt)
⇒góc FAG = góc CAG
Xét hai tam giác vuông: ∆AGF và ∆AGC có:
AG chung
góc FAG = góc CAG (cmt)
⇒∆AGF = ∆AGC (cạnh góc vuông - góc nhọn kề)
⇒AF = AC (hai cạnh tương ứng)
Mà AF = AB + BF
AC = AE + EC
AB = AE
⇒BF = CE
Cho hình thoi ABCD. Lấy điểm E trên cạnh AB sao cho \(\dfrac{AE}{AB}=\dfrac{2}{3}\) và điểm F trên cạnh CD sao cho \(\dfrac{DF}{DC}=\dfrac{1}{3}\)
a) Tứ giác AECF, EBFD là hình gì?
b) AD và EF kéo dài gặp nhau ở H. Tính \(\dfrac{HD}{HA}\)
c) Chứng minh HC vuông góc với AC và F là trọng tâm tam giác HDB
a) -Có: \(\dfrac{DF}{DC}=\dfrac{1}{3}\) mà \(AE+EB=AB\) nên \(\dfrac{CF}{DC}=\dfrac{2}{3}\).
\(AB=DC\)(ABCD là hình thoi) \(\Rightarrow\dfrac{CF}{AB}=\dfrac{2}{3}\)
Mà \(\dfrac{AE}{AB}=\dfrac{2}{3}\) (gt) nên \(AE=CF\).
Mà EB//DF (ABCD là hình thoi) nên \(AECF\) là hình hình bình.
-Tương tự như vậy, EBFD là hình bình hành.
b) -Có: \(\dfrac{AE}{AB}=\dfrac{2}{3}\) mà \(AE+EB=AB\) nên \(\dfrac{EB}{AB}=\dfrac{1}{3}\Rightarrow\dfrac{EB}{AE}=\dfrac{1}{2}\).
-Có: \(\dfrac{DF}{DC}=\dfrac{1}{3}\) mà \(\dfrac{EB}{DC}=\dfrac{1}{3}\left(\dfrac{EB}{AB}=\dfrac{1}{3};AB=CD\right)\)
\(\Rightarrow DF=EB\) nên \(\dfrac{DF}{AE}=\dfrac{1}{2}\).
-Xét △AEH có: DF//AE (ABCD là hình thoi).
\(\Rightarrow\dfrac{DF}{AE}=\dfrac{HD}{HA}=\dfrac{DH}{AH}=\dfrac{1}{2}\) (định lí Ta-let).
c) -Có \(\dfrac{DH}{AH}=\dfrac{1}{2}\) nên D là trung điểm AH.
\(\Rightarrow AD=DH=CD=\dfrac{1}{2}AH\)
-Xét △ACH có:
CD là trung tuyến ứng với cạnh AH (D là trung điểm AH)
Mà \(CD=\dfrac{1}{2}AH\) (cmt)
Nên △ACH vuông tại C.
\(\Rightarrow\) HC vuông góc với AC.
-Gọi G là giao điểm của CD và BH.
-Có \(DH=CD\) (cmt) và \(CD=BC\) (ABCD là hình thoi)
Nên \(DH=BC\) mà DH//BC (ABCD là hình thoi).
\(\Rightarrow\) BDHC là hình bình hành.
-Mà G là giao điểm của CD và BH nên G là trung điểm CD và BH
\(\Rightarrow GD=\dfrac{1}{2}DC=\dfrac{1}{2}.3DF=\dfrac{3}{2}DF\)
\(\Rightarrow DF=\dfrac{2}{3}GD\).
-Xét △HDB có:
DG là trung tuyến (G là trung điểm BH).
F thuộc DG.
\(DF=\dfrac{2}{3}GD\) (cmt).
Nên F là trọng tâm của tam giác HDB.