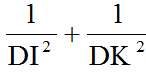Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.a) ΔANM là tam giác gì?b) Cmr: khi điểm M di động trên cạnh BC thì dfrac{1}{AM^2}+dfrac{1}{AE^2}không đổi A B C D N M
Đọc tiếp
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.
a) ΔANM là tam giác gì?
b) Cmr: khi điểm M di động trên cạnh BC thì \(\dfrac{1}{AM^2}+\dfrac{1}{AE^2}\)không đổi
Cho hình vuông ABCD . Lấy I thuộc BC.
Qua A kẻ đường thẳng vuông góc với AI cắt DC tại N
AI cắt đường thẳng DC tại M
a,CM : tam giác ANI cân
b,CM : AI\(\cdot\)AM=AB\(\cdot\)NM
c,CM : Khi điểm I thay đổi trên BC thì \(\dfrac{1}{AI^2}+\dfrac{1}{AM^2}\) không đổi
Cho hình bình hành ABCD. Hai đường thẳng đi qua tâm của hình bình hành chia nó thành bốn tứ giác có diện tích bằng nhau. Đường thẳng thứ nhất cắt BC tại E, đường thẳng thứ 2 cắt CD tại F. Chứng minh E chia cạnh BC và F chia cạnh CD theo cùng một tỉ số.
Cho hình vuông ABCD và điểm M thuộc cạnh BC. AM cắt DC tại N.
Chứng minh rằng: \(\dfrac{1}{AB^2}\)= \(\dfrac{1}{AM^2}\)+\(\dfrac{1}{AN^2}\)
cho hình vuông ABC , E à điểm năm giữa A và B . Tia DEvà tia CB cắt nhau ở K. kẻ qua D 1 đường thẳng vuống góc với DE cắt đường thẳng BC tại H
CMR: 1) tam giác DEH cân
2) 1 phần DE mũ 2 cộng 1 phần DK mũ 2 không đổi khi E thay đổi trên cạnh AB
Cho tam giác ABC (AB<AC) có đường cao AH và đường phân giác AD. Trên cạnh AC, lấy 1 điểm E sao cho AE=AB. Nối BE cắt AH tại I.
a) Chứng minh \(\dfrac{HB}{HC}=\dfrac{IB^2}{IE^2}\)
b) Cho DB= 15cm, DC=20cm. Tính chu vi và diện tích của tứ giác AEDI
Cho hình thoi ABCD có góc A = 120 độ . Vẽ tia Ax nằm trong hình thoi sao cho góc xAB = 15 độ . Tia Ax cắt BC tại I và cắt đường thẳng CD tại K . CMR \(\dfrac{4}{3AB^2}=\dfrac{1}{AI^2}+\dfrac{1}{AK^2}\)
giúp mk bài này vs Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổngkhông đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
giúp mk bài này vs
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
không đổi khi I thay đổi trên cạnh AB.
Cho hình vuồn ABCD, M ∈ BC, AM cắt tia DC tại N. Chứng minh \(\dfrac{1}{AB^2}=\dfrac{1}{AM^2}+\dfrac{1}{AN^2}\)