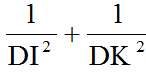Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.a) ΔANM là tam giác gì?b) Cmr: khi điểm M di động trên cạnh BC thì dfrac{1}{AM^2}+dfrac{1}{AE^2}không đổi A B C D N M
Đọc tiếp
Cho hình vuông ABCD lấy điểm M ∈ BC vẽ AN ⊥ AM; N ∈ CD; tia AM cắt đường thẳng CD tại E.
a) ΔANM là tam giác gì?
b) Cmr: khi điểm M di động trên cạnh BC thì \(\dfrac{1}{AM^2}+\dfrac{1}{AE^2}\)không đổi
cho hình vuông ABC , E à điểm năm giữa A và B . Tia DEvà tia CB cắt nhau ở K. kẻ qua D 1 đường thẳng vuống góc với DE cắt đường thẳng BC tại H
CMR: 1) tam giác DEH cân
2) 1 phần DE mũ 2 cộng 1 phần DK mũ 2 không đổi khi E thay đổi trên cạnh AB
Cho hình vuông ABCD và điểm M thuộc cạnh BC. AM cắt DC tại N.
Chứng minh rằng: \(\dfrac{1}{AB^2}\)= \(\dfrac{1}{AM^2}\)+\(\dfrac{1}{AN^2}\)
(2,5 điểm) Cho triangle ABC vuông tại A, đường cao AH, đường trung tuyến. AM 1 ) Biết BC = 10 cm, BH = 3.6cm Tỉnh độ dài đoạn thẳng AB, AH và số đo góc HAM ( làm ròn số đo góc đến phút) b) từ B kẻ BE vuông góc AM (E thuộc AM ) BE cắt cắt AH tại D. Chứng minh rằng DM II AC HD = DM * sin C Lấy điểm K trên cạnh BE sao cho hat AKM = 90 deg Chứng minh AE. ME = BE .DE VÀ S² AMK =S² AMB. S AMD
giúp mk bài này vs Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổngkhông đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
giúp mk bài này vs
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
không đổi khi I thay đổi trên cạnh AB.
Cho hình vuông ABCD trên CD lấy điểm I, AI cắt BC tại N
Cmr: \(\dfrac{1}{AB^2}\) = \(\dfrac{1}{AI^2}\) +\(\dfrac{1}{AN^2}\)
AB2 = BN . DI
Giúp mình với ạ mình đang cần gấp !!!!!
Qua đỉnh A của hình vuông ABCD cạnh bằng a, vẽ đường thẳng cắt BC ở E và cắt đường thẳng DC ở F. Chứng minh: \(\dfrac{1}{AE^{2^{ }}}+\dfrac{1}{ÀF^2}=\dfrac{1}{a^2}\)
help me
cho tam giác ABC vuông tại A có đường cao AH. Gọi E và F lần lượt là hình chiếu của H trên AB,AC. cho BH= 3cm, CH= 12cm
a, tính độ dài các cạnh AB,AC
b, chứng minh HF= 2HE
c, từ C kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AB tại I, kẻ AK vuông góc với CI tại K. chứng minh
CI^3/CB^3= IK/BH
Cho hình chữ nhật ABCD (AB lớn hơn AC) . Kẻ AH vuông góc BD tại H . AH cắt DC tại K và cắt đường thẳng BC tại M A) Chứng minh DH.DB=AH.AK và BC.BD=AH.AM B) Chứng minh AD bình = DK.DC C) Chứng minh AH bình= HK.HM