Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

Xét tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\).

Đặt cạnh huyền \(BC=a\), các cạnh góc vuông \(AB=c;AC=b\); đường cao ứng với cạnh huyền \(AH=h\); các đoạn \(BH=c';CH=b'\) lần lượt là hình chiếu của \(AB,AC\) trên cạnh huyền.

1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

Xét tam giác \(ABH\) và tam giác \(CBA\) có:

\(\widehat{B}\) chung;

\(\widehat{AHB}=\widehat{CAB}=90^0\)

\(\Rightarrow\Delta ABH\) đồng dạng với \(\Delta CBA\) (góc - góc)

\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BC}{AB}\Rightarrow AB^2=BC.BH\Rightarrow c^2=ac'\).

Hoàn toàn tương tự, ta chứng minh được \(\Delta ACH\) đồng dạng với \(\Delta BCA\) (góc - góc)

\(\Rightarrow\dfrac{AC}{CH}=\dfrac{BC}{AC}\Rightarrow AC^2=CH.BC\Rightarrow b^2=ab'\).

Như vậy, ta có Định lí 1:

Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu tương ứng của cạnh góc vuông đó trên cạnh huyền.

\(b^2=ab';c^2=ac'\)

Ví dụ: Tam giác \(ABC\) vuông tại \(A\), cạnh huyền \(BC=8\). Kẻ \(AH\) vuông góc \(BC\). Biết \(BH=3\). Tính độ dài các cạnh \(AB,AC\)?

Lời giải: 

Ta có: \(BH+CH=BC\Rightarrow CH=BC-BH=8-3=5\).

Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta có: 

\(\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB^2=8.3=24\\AC^2=8.5=40\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{24}=2\sqrt{6}\\AC=\sqrt{40}=2\sqrt{10}\end{matrix}\right.\).

2. Một số hệ thức liên quan tới đường cao

Xét tam giác \(AHB\) và tam giác \(CHA\) có:

\(\widehat{AHB}=\widehat{CHA}=90^0\);

\(\widehat{BAH}=\widehat{ACH}\) (cùng phụ với góc \(ABH\))

\(\Rightarrow\Delta AHB\) đồng dạng \(\Delta CHA\) (góc - góc)

\(\Rightarrow\dfrac{AH}{HB}=\dfrac{CH}{AH}\Rightarrow AH^2=BH.CH\Rightarrow h^2=b'.c'\).

Như vậy ta có Định lí 2:

Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.

\(h^2=b'.c'\)

Mặt khác, ta lại có: 

\(\left\{{}\begin{matrix}S_{ABC}=\dfrac{1}{2}AB.AC\\S_{ABC}=\dfrac{1}{2}AH.BC\end{matrix}\right.\Rightarrow AB.AC=AH.BC\Rightarrow bc=ah\)

Do đó, ta có Định lí 3: 

Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng với nó.

\(bc=ah\)

Từ định lí 3, ta có: \(ah=bc\Rightarrow a^2h^2=b^2c^2\)

Mà \(a^2=b^2+c^2\) (theo định lí Pytago) \(\Rightarrow\left(b^2+c^2\right)h^2=b^2c^2\)

\(\Rightarrow\dfrac{1}{h^2}=\dfrac{b^2+c^2}{b^2c^2}\Rightarrow\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\).

Như vậy, ta có Định lí 4:

Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.

\(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\)

Ví dụ: Xác định các giá trị \(x\) và \(y\) trong hình vẽ sau

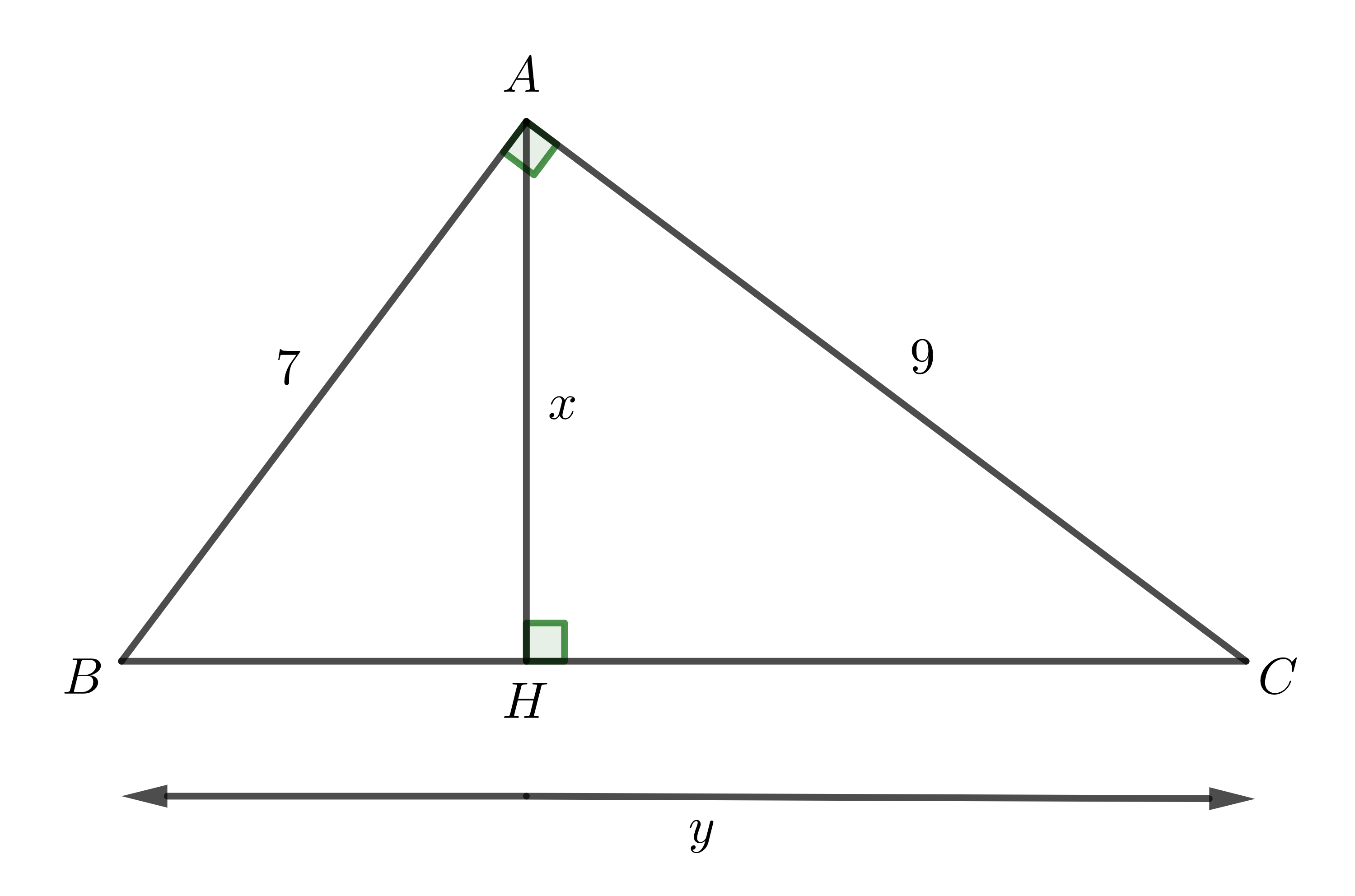
Lời giải:

Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta có:

\(\dfrac{1}{x^2}=\dfrac{1}{7^2}+\dfrac{1}{9^2}\Rightarrow\dfrac{1}{x^2}=\dfrac{130}{3969}\)

\(\Rightarrow x^2=\dfrac{3969}{130}\Rightarrow x=\dfrac{63}{\sqrt{130}}\).

Mặt khác: \(xy=7.9\Rightarrow y=\dfrac{7.9}{x}=\dfrac{63}{\dfrac{63}{\sqrt{130}}}\Rightarrow y=\sqrt{130}\).

Vậy \(x=\dfrac{63}{\sqrt{130}};y=\sqrt{130}\).