Bài 2: Tỉ số lượng giác của góc nhọn

1. Khái niệm tỉ số lượng giác của một góc nhọn

a) Mở đầu

- Cho tam giác \(ABC\) vuông tại \(A\). Xét góc nhọn \(B\) của nó. Khi đó: \(AB\) được gọi là cạnh kề của góc \(B\), \(AC\) được gọi là cạnh đối của góc \(B\).

- Ta đã biết, hai góc vuông đồng dạng với nhau khi và chỉ khi chúng có cùng số đo một góc nhọn, hoặc tỉ số giữa cạnh đối và cạnh kề của một góc nhọn trong tam giác là như nhau. Như vậy, tỉ số giữa cạnh đối và cạnh kề của một góc nhọn trong tam giác vuông đặc trưng cho độ lớn của góc  nhọn đó. 

Ví dụ: Với tam giác vuông cân, ta có hai cạnh góc vuông bằng nhau, hai góc nhọn đều bằng \(45^0\), như vậy tỉ số giữa cạnh đối và cạnh kề của góc \(45^0\) là 1.

- Ngoài ra, ta còn xét tỉ số giữa cạnh kề với cạnh đối, cạnh đối với cạnh huyền, cạnh kề với cạnh huyền của một góc nhọn trong tam giác vuông. Các tỉ số này chỉ thay đổi khi độ lớn của góc nhọn đang xét thay đổi. Ta gọi chúng là tỉ số lượng giác của góc nhọn đó.

b) Định nghĩa

Cho tam giác vuông với một góc nhọn là \(\alpha\). Trên hình vẽ, ta xác định được cạnh đối và cạnh kề của \(\alpha\).

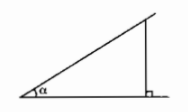
Khi đó:

• Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha\), kí hiệu \(\sin\alpha\).
• Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha\), kí hiệu \(\cos\alpha\).
• Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha\), kí hiệu \(\tan\alpha\).
• Tỉ số giữa cạnh kề và cạnh đối gọi là côtang của góc \(\alpha\), kí hiệu \(\cot\alpha\).

Ví dụ: với tam giác \(ABC\) vuông tại \(A\) (hình vẽ trên), ta có:

\(\sin B=\dfrac{AC}{BC};\cos B=\dfrac{AB}{BC};\tan B=\dfrac{AC}{AB};\cot B=\dfrac{AB}{AC}\)

Chú ý: Từ định nghĩa, ta thấy: Tỉ số lượng giác của một góc nhọn luôn là số dương. Hơn nữa, với \(\alpha\) là góc nhọn thì \(\sin\alpha< 1;\cos\alpha< 1\).

Quay trở lại ví dụ trên, ta có thể thấy:

+) \(\sin^2B+\cos^2B=\dfrac{AC^2}{BC^2}+\dfrac{AB^2}{BC^2}=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\) (áp dụng định lí Pytago).

+) \(\tan B=\dfrac{AC}{AB}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{\sin B}{\cos B}\).

+) \(\cot B=\dfrac{AB}{AC}=\dfrac{AB}{BC}:\dfrac{AC}{BC}=\dfrac{\cos B}{\sin B}\).

+) \(\tan B=\dfrac{1}{\cot B}=\dfrac{AC}{AB}\Rightarrow\tan B.\cot B=1\).

Các biểu thức trên không phụ thuộc vào vị trí và độ lớn của góc \(B\). Như vậy, một cách tổng quát:

Với \(\alpha\) là góc nhọn, ta luôn có: 

• \(\sin^2\alpha+\cos^2\alpha=1\).
• \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\); \(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}\).
• \(\tan\alpha.\cot\alpha=1\).

Từ các đẳng thức trên, khi biết một tỉ số lượng giác của một góc nhọn, ta có thể tìm được các tỉ số còn lại.

Ví dụ: Cho góc nhọn \(\beta\) có \(\sin\beta=\dfrac{3}{5}\). Tính các tỉ số lượng giác còn lại của \(\beta\)?

Ta có: \(\sin^2\beta+\cos^2\beta=1\)\(\Rightarrow\cos^2\beta=1-\sin^2\beta=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)

Mà \(0< \cos\beta< 1\Rightarrow\cos\beta=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}\).

\(\Rightarrow\tan\beta=\dfrac{\sin\beta}{\cos\beta}=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4};\cot\beta=\dfrac{1}{\tan\beta}=\dfrac{4}{3}\).

Chú ý:

• Nếu hai góc nhọn \(\alpha,\beta\) có \(\sin\alpha=\sin\beta\) (hoặc \(\cos\alpha=\cos\beta\), \(\tan\alpha=\tan\beta\), \(\cot\alpha=\cot\beta\)) thì \(\alpha=\beta\) và chúng là hai góc nhọn tương ứng của hai góc vuông đồng dạng.
• Khi biết một góc nhọn, ta có thể tính được các tỉ số lượng giác của nó (bằng cách ghép vào tam giác vuông có góc nhọn tương ứng). Ngược lại, khi biết một tỉ số lượng giác, ta có thể dựng góc nhọn đó.

2. Tỉ số lượng giác của hai góc phụ nhau

Cho tam giác \(ABC\) vuông tại \(A\), kí hiệu góc \(B\) là \(\alpha\), góc \(C\) là \(\beta\).

Ta thấy:

\(\sin\alpha=\dfrac{AC}{BC};\cos\beta=\dfrac{AC}{BC}\Rightarrow\sin\alpha=\cos\beta\);

\(\cos\alpha=\dfrac{AB}{BC};\sin\beta=\dfrac{AB}{BC}\Rightarrow\cos\alpha=\sin\beta\);

\(\tan\alpha=\dfrac{AC}{AB};\cot\beta=\dfrac{AC}{AB}\Rightarrow\tan\alpha=\cot\beta\);

\(\cot\alpha=\dfrac{AB}{AC};\tan\beta=\dfrac{AB}{AC}\Rightarrow\cot\alpha=\tan\beta\).

\(\alpha,\beta\) là các góc phụ nhau. Ta thấy hai góc phụ nhau bất kì bao giờ cũng là các góc nhọn trong một tam giác vuông, nên các đẳng thức trên không phụ thuộc vào đại diện \(\alpha,\beta\).

Do đó, ta có định lí:

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Ví dụ: Do \(30^0+60^0=90^0\) nên \(\sin30^0=\cos60^0;\tan30^0=\cot60^0\). Do \(25^0+65^0=90^0\) nên \(\cos25^0=\sin65^0;\cot25^0=\tan65^0\); ...

Thông qua thực hành, ta tìm được bảng tỉ số lượng giác của một số góc nhọn đặc biệt như sau: