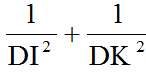Question

giúp mk bài này vs

 Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:

a) Tam giác DIL là một tam giác cân

b) Tổng

không đổi khi I thay đổi trên cạnh AB.

Answer 1

a) \(_{\Delta}\) ADI và  \(\Delta\)  DCL có:

góc DAI = góc DCL = \(90^0\) (gt)

AD=CD( gt)

góc ADI = góc CDL ( cùng phụ góc IDC)

=>  \(\Delta\)  ADI = \(\Delta\) CDL ( ch-gn) => DI =DL ( cạnh tương ứng) 

=> Tam giác DIL cân 

b)  Tam giác DLK vuông tại D=>  \(\dfrac{1}{C\text{D}^2}=\dfrac{1}{DK^2}+\dfrac{1}{DL^2}\)

=> \(\dfrac{1}{C\text{D}^2}=\dfrac{1}{DK^2}+\dfrac{1}{DI^2}\)  ( DI = DL)