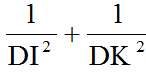18 tháng 7 2023 lúc 19:05
Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
cho tam giác MNP vuông tại a đường cao MI TỪ I kẻ IE vuông góc với MN , IF vuông góc với MP . O là trung điểm của NP . có tam giác MEF đồng dạng với tam giác MPN .CMR MO vuông góc với EF
cho tam giác MNP vuông tại a đường cao MI TỪ I kẻ IE vuông góc với MN , IF vuông góc với MP . O là trung điểm của NP . Có tam giác MEF đồng dạng với tam giác MPN .CMR MO vuông góc với EF
cho tam giác MNP vuông tại a đường cao MI TỪ I kẻ IE vuông góc với MN , IF vuông góc với MP . O là trung điểm của NP . có tam giác MEF đồng dạng với tam giác MPN .CMR MO vuông góc với EF
cho tam giác MNP vuông tại a đường cao MI TỪ I kẻ IE vuông góc với MN , IF vuông góc với MP . O là trung điểm của NP . có tam giác MEF đồng dạng với tam giác MPN .CMR MO vuông góc với EF
cho tam giác MNP vuông tại a đường cao MI TỪ I kẻ IE vuông góc với MN , IF vuông góc với MP . O là trung điểm của NP . có tam giác MEF đồng dạng với tam giác MPN .CMR MO vuông góc với EF Giai bài này hộ e vs ạ
21 tháng 9 2021 lúc 16:58
giúp mk bài này vs Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổngkhông đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
giúp mk bài này vs
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
không đổi khi I thay đổi trên cạnh AB.
cho tam giác ABC vuông tại A có đường cao AH. Gọi E và F lần lượt là hình chiếu của H trên AB,AC. cho BH= 3cm, CH= 12cm
a, tính độ dài các cạnh AB,AC
b, chứng minh HF= 2HE
c, từ C kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AB tại I, kẻ AK vuông góc với CI tại K. chứng minh
CI^3/CB^3= IK/BH
Cho tam giác ABC nhọn có AH là đường cao kẻ HM vuông góc với AB tại M, HN vuông góc với AC tại N. Chứng minh AB.AM=AC.AN.
Cho tam giác 𝐴𝐵𝐶 có ba góc nhọn, đường cao 𝐵𝐸. Từ E kẻ 𝐸𝐻, 𝐸𝐾 vuông góc với 𝐵𝐴, 𝐵𝐶. a) Chứng minh 𝐵𝐻. 𝐵𝐴 = 𝐵𝐾. 𝐵𝐶 b) Chứng minh ∆𝐵𝐻𝐾~∆𝐵𝐶𝐴. c) Kẻ 𝐶𝐹 vuông góc với 𝐴𝐵, gọi 𝐼 là trung điểm của 𝐸𝐹. Chứng minh ba điểm 𝐻,𝐼,𝐾 thẳng hàng.