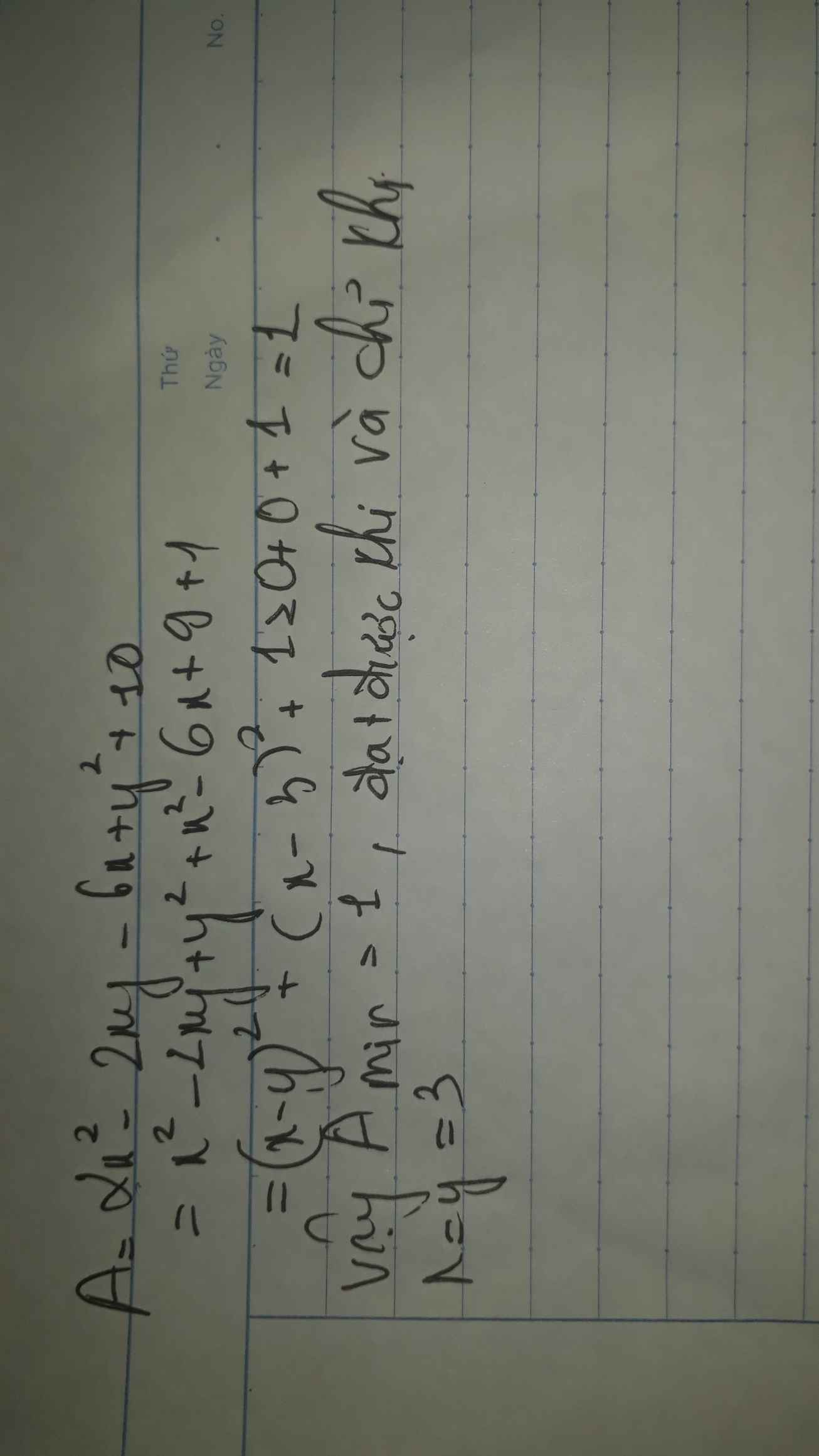A= 2x^2 + y^2 - 2xy -2x+3

A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2

A= (x-y)^2 + (x-1)^2 + 2

(x-y)^2> hoặc = 0 với mọi giá trị của x

(x-1)^2 > hoặc =0 với mọi giá trị của x

=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x

=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2

=> A lớn hơn hoặc bằng 2

=> GTNN của A=2 tại x=y=1

A= -x²+2x+3

=>A= -(x²-2x+3)

=>A= -(x²-2.x.1+1+3-1)

=>A=-[(x-1)²+2]

=>A= -(x+1)²-2

Vì -(x+1)² ≤0=> A≤-2

Dấu "=" xảy ra khi

-(x+1)²=0 => x=-1

Vây A lớn nhất= -2 khi x= -1

B=x²-2x+4y²-4y+8

=> B= (x²-2x+1)+(4y²-4y+1)+6

=> B=(x-1)²+(2y+1)²+6

=> B lớn nhất=6 khi x=1 và y=-1/2

Xét biểu thức \(A=x\left(x-3\right)\left(x-4\right)\left(x-7\right)=\left(x^2-7x\right)\left(x^2-7x+12\right)\)

Đặt \(x^2-7x+6\rightarrow t\)Khi đó \(A=\left(t-6\right)\left(t+6\right)=t^2-36\ge-36\)

Dấu "=" xảy ra khi và chỉ khi \(t=0\)hay \(x^2-7x+6=0=>\left(x-6\right)\left(x-1\right)=0=>\orbr{\begin{cases}x=6\\x=1\end{cases}}\)

Vậy GTNN của biểu thức \(A=-36\)đạt được khi \(x=6orx=1\)

Xét biểu thức \(B=2x^2+y^2-2xy-2x+3=\left(x^2-2xy+y^2\right)+x^2-2x+1+2\)

\(=\left(x-y\right)^2+\left(x-1\right)^2+2\ge2\)

Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-y=0\\x-1=0\end{cases}< =>\hept{\begin{cases}1-y=0\\x=1\end{cases}}< =>\hept{\begin{cases}x=1\\y=1\end{cases}< =>x=y=1}}\)

Vậy GTNN của biểu thức \(B=2\)đạt được khi \(x=y=1\)

Xét biểu thức \(C=x^2+y^2-3x+3y=\left(x^2-3x+\frac{9}{4}\right)+\left(y^2+3y+\frac{9}{4}\right)-\frac{9}{2}\)

\(=\left(x^2-3x+\frac{3^2}{2^2}\right)+\left(y^2+3y+\frac{3^2}{2^2}\right)-\frac{9}{2}=\left(x-\frac{3}{2}\right)^2+\left(y+\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)

Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-\frac{3}{2}=0\\y+\frac{3}{2}=0\end{cases}}< =>\hept{\begin{cases}x=\frac{3}{2}\\y=-\frac{3}{2}\end{cases}< =>x=-y=\frac{3}{2}}\)

Vậy GTNN của biểu thức \(C=-\frac{9}{2}\)đạt được khi \(x=-y=\frac{3}{2}\)

\(A=2x^2+y^2-2x+2xy+2y+3=y^2+2y\left(x+1\right)+\left(x+1\right)^2+\left(x^2-4x+4\right)-2=\left(y+x+1\right)^2+\left(x-2\right)^2-2\ge-2\)

\(minA=-2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)

\(P=x^3+2021xy+y^3\)

\(=\left(x+y\right)^3-3xy\left(x+y\right)+2021xy\)

\(=\left(\dfrac{2021}{3}\right)^3\)

\(=\dfrac{8254655261}{27}\)

b) Ta có: \(B=x^2+2x+y^2-4y+6\)

\(=x^2+2x+1+y^2-4y+4+1\)

\(=\left(x+1\right)^2+\left(y-2\right)^2+1\ge1\forall x,y\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)

Vậy: \(B_{min}=1\) khi (x,y)=(-1;2)

c) Ta có: \(C=4x^2+4x+9y^2-6y-5\)

\(=4x^2+4x+1+9y^2-6y+1-7\)

\(=\left(2x+1\right)^2+\left(3y-1\right)^2-7\ge-7\forall x,y\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Vậy: \(C_{min}=-7\) khi \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)

\(A=2x^2+x=2\left(x^2+\dfrac{1}{2}x\right)=2\left(x^2+2.\dfrac{1}{4}x+\dfrac{1}{16}-\dfrac{1}{16}\right)\)

\(=2\left[\left(x+\dfrac{1}{4}\right)^2-\dfrac{1}{16}\right]\ge-\dfrac{1}{8}\) dấu"=' xảy ra<=>x=\(-\dfrac{1}{4}\)

\(B=x^2+2x+y^2-4y+6\)

\(=x^2+2x+1+y^2-4y+4+1=\left(x+1\right)^2+\left(y-2\right)^2+1\)

\(\ge1\) dấu"=" xảy ra<=>x=-1;y=2

\(C=4x^2+4x+9y^2-6y-5\)

\(=4x^2+4x+1+9y^2-6y+1-7\)

\(=\left(2x+1\right)^2+\left(3y-1\right)^2-7\ge-7\)

dấu"=" xảy ra<=>x=\(-\dfrac{1}{2},y=\dfrac{1}{3}\)

\(D=\left(2+x\right)\left(x+4\right)-\left(x-1\right)\left(x+3\right)^2\)

=\(x^2+6x+8-\left(x-1\right)\left(x+3\right)^2\)

\(=\left(x+3\right)^2-1-\left(x-1\right)\left(x+3\right)^2\)

\(=\left(x+3\right)^2\left(2-x\right)-1\ge-1\)

dấu"=" xảy ra\(< =>\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)

\(a,A=x\left(x-3\right)\left(x-4\right)\left(x-7\right)\)

\(=x\left(x-7\right)\left(x-3\right)\left(x-4\right)\)

\(=\left(x^2-7x\right)\left(x^2-7x+12\right)\)

Đặt \(x^2-7x+6=t\)ta có:

\(A=\left(t-6\right)\left(t+6\right)=t^2-36\ge-36\)

Vậy \(Min_A=-36\)khi \(t=0\Leftrightarrow x^2-7x+6=0\)

\(\Leftrightarrow x^2-6x-x+6=0\)

\(\Leftrightarrow x\left(x-6\right)-\left(x-6\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-6\right)=0\Rightarrow\left[{}\begin{matrix}x-1=0\\x-6=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\)\(b,B=2x^2+y^2-2xy-2x+3\)

\(=\left(x^2-2xy+y^2\right)+\left(x^2-2x+1\right)+2\)

\(\Leftrightarrow\left(x-y\right)^2+\left(x-1\right)^2+2\ge2\)

Vậy \(Min_B=2\)khi \(\left[{}\begin{matrix}x-y=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y=1\\x=1\end{matrix}\right.\)

\(c,C=x^2+y^2-3x+3y\)

\(=\left(x^2-3x+\dfrac{9}{4}\right)+\left(y^2+3y+\dfrac{9}{4}\right)-\dfrac{9}{2}\)

\(=\left(x-\dfrac{3}{2}\right)^2+\left(y+\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge\dfrac{-9}{2}\)

Vậy \(Min_C=\dfrac{-9}{2}\)khi \(\left[{}\begin{matrix}x-\dfrac{3}{2}=0\\y+\dfrac{3}{2}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\y=-\dfrac{3}{2}\end{matrix}\right.\)

\(a.\left(x^2+4x+4\right)+\left(x^2-6x+9\right)=2x^2+14x\)

\(x^2+4x+4+x^2-6x+9-2x^2-14x=0\)

\(-18x+13=0\)

\(x=\dfrac{13}{18}\)

Vậy \(S=\left\{\dfrac{13}{18}\right\}\)

\(b.\left(x-1\right)^3-125=0\)

\(\left(x-1\right)^3=125\)

\(x-1=5\)

\(x=6\)

Vậy \(S=\left\{6\right\}\)

\(c.\left(x-1\right)^2+\left(y +2\right)^2=0\)

\(Do\left(x-1\right)^2\ge0\forall x;\left(y+2\right)^2\ge0\forall y\)

\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2\ge0\forall x,y\)

Mà \(\left(x-1\right)^2+\left(y+2\right)^2=0\)

\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

Vậy \(S=\left\{1;-2\right\}\)

\(d.x^2-4x+4+x^2-2xy+y^2=0\)

\(\left(x-2\right)^2+\left(x-y\right)^2=0\)

\(\Rightarrow\left[{}\begin{matrix}\left(x-2\right)^2=0\\\left(x-y\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

Vậy \(S=\left\{2;2\right\}\)

`A=2x^2-2xy-6x+y^2+10`

`A=x^2-2xy+y^2+x^2-6x+10`

`A=(x-y)^2+x^2-6x+9+1`

`A=(x-y)^2+(x-3)^2+1`

Vì `(x-y)^2+(x-3)^2>=0=>A>=1`

Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`

A=\(\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)+1=\left(x-y\right)^2+\left(x-3\right)^2+1\ge1\\ \)

dấu= xảy ra khi x=y=3

tick mik nha

\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)

Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)

\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)