Cho \(B=\dfrac{5}{\sqrt{x}-1}\). Tìm \(x\in\mathbb{Z}\) để B có giá trị nguyên ?

Những câu hỏi liên quan
Cho \(B=\dfrac{2}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
Tìm \(x\in Z\) để B có giá trị nguyên
\(B=\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}-2+2\sqrt{x}+x-3\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
Để B nguyên thì \(\sqrt{x}-3\in\left\{1;-1;5\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;8\right\}\)
hay \(x\in\left\{16;4;64\right\}\)
Đúng 0
Bình luận (0)
Cho \(B=\dfrac{5}{\sqrt{x}-1}\) Tìm x thuộc Z để B có giá trị nguyên.
Để B có nghĩa thì x ≥ 0 và x ≠ 1
\(B=\dfrac{5}{\sqrt{x}-1}\) nguyên khi \(\sqrt{x}-1\) thuộc ước của 5
⇒ \(\sqrt{x}-1\) ∈ \(\left\{1,-1,5,-5\right\}\)
\(TH1:\sqrt{x}-1=1\Rightarrow x=4\)
\(TH2:\sqrt{x}-1=-1\Rightarrow x=0\)
\(TH3:\sqrt{x}-1=5\Rightarrow x=36\)
\(TH4:\sqrt{x}-1=-5\Rightarrow x=-4\) (loại vì x ≥ 0)
Vậy \(x\in\left\{0,4,36\right\}\)
Đúng 3
Bình luận (0)
\(ĐK:x\ge0;x\ne1\\ B\in Z\Leftrightarrow\sqrt{x}-1\inƯ\left(5\right)=\left\{-1;1;5\right\}\left(\sqrt{x}-1\ge-1\right)\\ \Leftrightarrow\sqrt{x}\in\left\{0;2;6\right\}\\ \Leftrightarrow x\in\left\{0;4;36\right\}\left(tm\right)\)
Đúng 3
Bình luận (0)
Cho \(A=\dfrac{\sqrt{x}-3}{2}\). Tìm \(x\in\mathbb{Z}\) và \(x< 30\) để A có giá trị nguyên ?
\(A=\dfrac{\sqrt{x}-3}{2}\) có giá trị nguyên nên \(\left(\sqrt{x}-3\right)⋮2.\)
Suy ra \(x\) là số chính phương lẻ.
Vì \(x< 30\) nên \(x\in\left\{1^2;3^2;5^2\right\}\)hay \(x\in\left\{1;9;25\right\}.\)
Đúng 0
Bình luận (0)
a, cho A dfrac{sqrt{x+1}}{sqrt{x-3}}. tìm x để A có giá trị nguyên ( x ϵ Z)b, Thực hiện phép tính: {[(2sqrt{2})^2 : 2,4] x [5,25 : (sqrt{7})^2]} : {[2dfrac{1}{7} : dfrac{left(sqrt{5}right)^2}{7}] : [2^2 : dfrac{left(2sqrt{2}right)^2}{sqrt{81}}]}
Đọc tiếp
a, cho A = \(\dfrac{\sqrt{x+1}}{\sqrt{x-3}}\). tìm x để A có giá trị nguyên ( x ϵ Z)
b, Thực hiện phép tính: {[(2\(\sqrt{2}\))\(^2\) : 2,4] x [5,25 : (\(\sqrt{7}\))\(^2\)]} : {[2\(\dfrac{1}{7}\) : \(\dfrac{\left(\sqrt{5}\right)^2}{7}\)] : [2\(^2\) : \(\dfrac{\left(2\sqrt{2}\right)^2}{\sqrt{81}}\)]}
a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
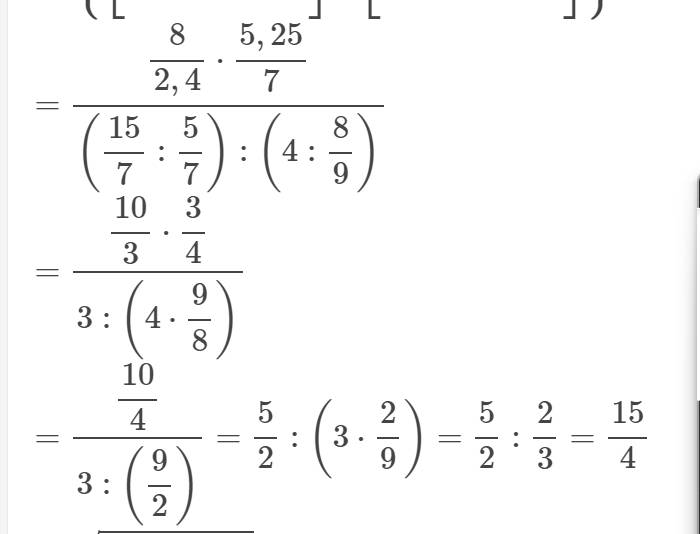
Đúng 0
Bình luận (0)
Cho biểu thức: Q = \(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-3\dfrac{\sqrt{x}-1}{x-5\sqrt{x}+6}\).
a) Tìm điều kiện xác định và rút gọn Q.
b) Tìm các giá trị của x để Q < -1.
c) Tìm các giá trị của x \(\in\) Z sao cho 2Q \(\in\) Z.
a, đk: \(x\ge0,x\ne9,x\ne4\)
\(Q=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-4-x+3\sqrt{x}-\sqrt{x}+3-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2-\sqrt{x}}{-\left(\sqrt{x}-3\right)\left(2-\sqrt{x}\right)}=\dfrac{-1}{\sqrt{x}-3}\)
b,\(Q< -1=>\dfrac{-1}{\sqrt{x}-3}+1< 0< =>\dfrac{-1+\sqrt{x}-3}{\sqrt{x}-3}< 0\)
\(< =>\dfrac{\sqrt{x}-4}{\sqrt{x}-3}< 0\)
\(=>\left\{{}\begin{matrix}\left[{}\begin{matrix}\sqrt{x}-4>0\\\sqrt{x}-3< 0\end{matrix}\right.\\\left[{}\begin{matrix}\sqrt{x}-4< 0\\\sqrt{x}-3>0\end{matrix}\right.\end{matrix}\right.\)\(< =>\left[{}\begin{matrix}\left\{{}\begin{matrix}x>16\\x< 9\end{matrix}\right.\\\left\{{}\begin{matrix}x< 16\\x>9\end{matrix}\right.\end{matrix}\right.\)\(< =>9< x< 16\)
c, \(=>2Q=\dfrac{-2}{\sqrt{x}-3}=1+\dfrac{1}{\sqrt{x}-3}\in Z\)
\(< =>\sqrt{x}-3\inƯ\left(1\right)=\left\{\pm1\right\}\)\(=>x\in\left\{16;4\right\}\)(loại 4)
=>x=16
Đúng 0
Bình luận (0)
a) \(Q=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-3\dfrac{\sqrt{x}-1}{x-5\sqrt{x}+6}\)
Ta có \(x-5\sqrt{x}+6=\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)\)
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\\sqrt{x}-3>0\\\sqrt{x}-2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x>9\\x>2\end{matrix}\right.\) \(\Leftrightarrow x>9\)
\(Q=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-3\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\left(x-4\right)-\left(x-2\sqrt{x}-3\right)-\left(3\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\) \(=\dfrac{-\sqrt{x}+2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\) \(=\dfrac{-\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\) \(=\dfrac{-1}{\left(\sqrt{x}-3\right)}=\dfrac{1}{3-\sqrt{x}}\)
b) \(Q< -1\Leftrightarrow\dfrac{1}{3-\sqrt{x}}< -1\) \(\Leftrightarrow\dfrac{1}{3-\sqrt{x}}+1< 0\) \(\Leftrightarrow\dfrac{4-\sqrt{x}}{3-\sqrt{x}}< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4-\sqrt{x}>0\\3-\sqrt{x}< 0\end{matrix}\right.\\\left\{{}\begin{matrix}4-\sqrt{x}< 0\\3-\sqrt{x}>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 16\\x>9\end{matrix}\right.\\\left\{{}\begin{matrix}x>16\\x< 9\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow9< x< 16\)
Vậy để \(Q< -1\) thì \(S=\left\{x/9< x< 16\right\}\)
c) \(2Q\in Z\Leftrightarrow\dfrac{2}{3-\sqrt{x}}\in Z\)
\(\Rightarrow3-\sqrt{x}\inƯ\left(2\right)\)\(\Leftrightarrow\left\{{}\begin{matrix}3-\sqrt{x}=2\\3-\sqrt{x}=-2\\3-\sqrt{x}=1\\3-\sqrt{x}=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\x=25\\x=4\\x=16\end{matrix}\right.\)
Kết hợp với ĐKXĐ,ta có để \(2Q\in Z\) thì \(x\in\left\{16;25\right\}\)
Đúng 0
Bình luận (0)
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{9;4\right\}\end{matrix}\right.\)
Ta có: \(Q=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{3\sqrt{x}-3}{x-5\sqrt{x}+6}\)
\(=\dfrac{x-4-x+2\sqrt{x}+2-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-\sqrt{x}+2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-1}{\sqrt{x}-3}\)
c) Để 2Q là số nguyên thì \(-2⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{4;2;5;1\right\}\)
\(\Leftrightarrow x\in\left\{16;25;1\right\}\)
Đúng 0
Bình luận (0)
Bài 1: Cho \(A=\frac{\sqrt{x}-3}{2}\) Tìm \(x\in Z\)và \(x< 30\)để A có giá trị nguyên
Bài 2: Cho \(B=\frac{5}{\sqrt{x}-1}\)Tìm \(x\in Z\)để B có giá trị nguyên
Cho hai bt A=\(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)và B=\(\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}+2}{x-4}\)
a) rút gọn B
b)tìm x thuộc Z để C= A(B-2) có giá trị nguyên
a) \(B=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}+2}{x-4}\left(đk:x\ge0,x\ne4\right)\)
\(=\dfrac{\sqrt{x}+\sqrt{x}+2}{x-4}.\dfrac{x-4}{\sqrt{x}+2}=\dfrac{2\sqrt{x}+2}{\sqrt{x}+2}\)
c) \(C=A\left(B-2\right)=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\left(\dfrac{2\sqrt{x}+2}{\sqrt{x}+2}-2\right)\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}.\dfrac{-2}{\sqrt{x}+2}=\dfrac{-2}{\sqrt{x}-2}\in Z\)
\(\Rightarrow\sqrt{x}-2\inƯ\left(2\right)=\left\{1;-1;2-2\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{3;1;4;0\right\}\)
\(\Rightarrow x\in\left\{0;1;9;16\right\}\)
Đúng 1
Bình luận (0)
Bài 8:Cho A=\(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)và B=\(\dfrac{\sqrt{x}+3}{\sqrt{x}+1}-\dfrac{5}{1-\sqrt{x}}+\dfrac{4}{x-1}\)(x≥0;x≠1)
a)Tính giá trị của A khi x=\(4+2\sqrt{3}\)
b)Rút gọn B
c)Tìm x để P=A.B có giá trị nguyên
Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên
A=\(\dfrac{x+2}{x-5}\) B=\(\dfrac{3x+1}{2-x}\) C=\(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\) D=\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+3}\)
\(A=\) \(\dfrac{x+2}{x-5}\)
\(=\dfrac{\left(x-5\right)+7}{x-5}\)
\(=1+\dfrac{7}{x-5}\)
để \(\dfrac{7}{x-5}\) ∈Z thì 7⋮x-5
⇒x-5∈\(\left(^+_-1,^+_-7\right)\)
Còn lại thì bạn tự tính nha
Đúng 1
Bình luận (0)























