Cho A=x^2-2mx+(m+1) tìm m để bt A có gtnn là 11
Ôn tập hệ hai phương trình bậc nhất hai ẩn
Lời giải:
$A=x^2-2mx+m+1=(x-m)^2+m+1-m^2\geq m+1-m^2$
$A_{\min}=m+1-m^2=11$
$\Leftrightarrow m^2-m+10=0$
$\Leftrightarrow (m-\frac{1}{2})^2=\frac{-39}{4}<0$ (vô lý)
Vậy hông tồn tại $m$ để $A_{\min}=11$
Đúng 1
Bình luận (0)
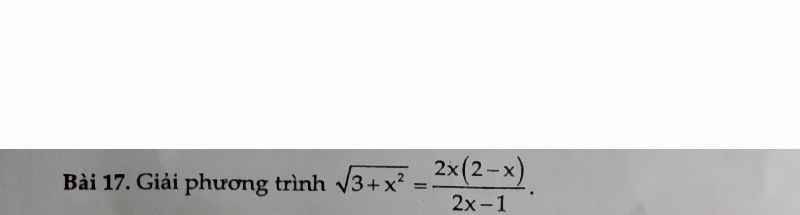 mn oi,giúp mình với
mn oi,giúp mình với
ĐKXĐ:\(x\ne\dfrac{1}{2}\)
PT đã cho tương đương với:
\(\sqrt{3+x^2}-2=\dfrac{2x\left(2-x\right)}{2x-1}-2\)
\(\Leftrightarrow\dfrac{x^2-1}{\sqrt{3+x^2}+2}=2\left[\dfrac{x\left(2-x\right)}{2x-1}-1\right]\)
\(\Leftrightarrow\dfrac{x^2-1}{\sqrt{3+x^2}+2}+\dfrac{2\left(x^2-1\right)}{2x-1}=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(\dfrac{1}{\sqrt{3+x^2}+2}+\dfrac{2}{2x-1}\right)=0\)
TH1:\(x^2-1=0\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
TH2:\(\dfrac{1}{\sqrt{3+x^2}+2}+\dfrac{2}{2x-1}=0\)
\(\Rightarrow2x-1+4+2\sqrt{3+x^2}=0\)
\(\Leftrightarrow2x+3+2\sqrt{3+x^2}=0\)
Ta có: \(2x+3+2\sqrt{3+x^2}\ge2x+3+2\sqrt{x^2}=2x+3+2\left|x\right|\ge2x+3-2x=3>0\)
nên trong TH2, pt vô nghiệm
Vậy pt đã cho có tập nghiệm \(S=\left\{-1;1\right\}\)
Đúng 2
Bình luận (0)
Trong một buổi liên hoan văn nghệ, phòng họp chỉ có 320 chỗ ngồi, nhưng số người tới dự hôm đó là 420 người. Do đó phải đặt thêm 1 dãy ghế và thu xếp mỗi dãy ghế thêm được 4 người ngồi nữa mới đủ. Hỏi lúc đầu trong phòng đó có bao nhiêu dãy ghế? ( Biết mỗi ghế chỉ có một người ngồi )
Gọi số dãy ghế ban đầu trong phòng là x(dãy)(ĐK: x>4)
Số dãy ghế lúc sau là x+1(dãy)
Số người ngồi trên 1 dãy ghế lúc đầu là \(\dfrac{320}{x}\left(người\right)\)
Số người ngồi trên 1 dãy ghế lúc sau là \(\dfrac{420}{x+1}\left(người\right)\)
Theo đề, ta có: \(\dfrac{420}{x+1}-\dfrac{320}{x}=4\)
=>\(\dfrac{420x-320x-320}{x\left(x+1\right)}=4\)
=>4x(x+1)=100x-320
=>x(x+1)=25x-80
=>x^2+x-25x+80=0
=>x^2-24x+80=0
=>(x-4)(x-20)=0
=>\(\left[{}\begin{matrix}x=4\left(loại\right)\\x=20\left(loại\right)\end{matrix}\right.\)
Vậy: ban đầu có 20 dãy ghế
Đúng 0
Bình luận (0)
Cho B=mx+n/x^2+1 tìm mn để B có gtnn là -1 gtln là 4 help meee
Bài 8: Cho hàm số y(2m-1)x+3 (d). Đi I) Vẽ đồ thị hàm số khi mfrac{3}{2}2) Tính góc tạo bởi đường thẳng d với trục Ox3) Tìm giá trị của m để (d) song song với đường thẳng y3x+1(d^{prime}) .4) Tìm m để (d) cắt (d1) y2x-3 tại điểm có hoành độ bằng 15) Tìm m để (d) cắt (d2) y2x-3 tại điểm có tung độ bằng 16) Gọi hai điểm A, B lần lượt là giao điểm của (d) với trục Ox và Oy. Tìm m để diện tích tam giác OAB bằng 3 (đvdt)7) Tìm m để khoảng cách từ gốc tọa độ O đến d là lớn nhất.Em cần gấp ạ
Đọc tiếp
Bài 8: Cho hàm số y=(2m-1)x+3 (d). Đi I) Vẽ đồ thị hàm số khi m=\frac{3}{2}
2) Tính góc tạo bởi đường thẳng d với trục Ox
3) Tìm giá trị của m để (d) song song với đường thẳng y=3x+1(d^{\prime}) .
4) Tìm m để (d) cắt (d1) y=2x-3 tại điểm có hoành độ bằng 1
5) Tìm m để (d) cắt (d2) y=2x-3 tại điểm có tung độ bằng 1
6) Gọi hai điểm A, B lần lượt là giao điểm của (d) với trục Ox và Oy. Tìm m để diện tích tam giác OAB bằng 3 (đvdt)
7) Tìm m để khoảng cách từ gốc tọa độ O đến d là lớn nhất.
Em cần gấp ạ
1: Khi m=3/2 thì \(\left(d\right):y=\left(2\cdot\dfrac{3}{2}-1\right)x+3=2x+3\)
2: \(tanx=a=2m-1\)
3:
Để hai đồ thị (d) và (d') song song với nhau thì:
\(2m-1=3\)
=>2m=4
=>m=2
4: Thay x=1 vào (d1), ta được:
\(y=2\cdot1-3=-1\)
Thay x=1 và y=-1 vào (d), ta được:
\(1\left(2m-1\right)+3=-1\)
=>2m+2=-1
=>2m=-3
=>\(m=-\dfrac{3}{2}\)
5: y=1
=>2x-3=1
=>2x=4
=>x=2
Thay x=2 và y=1 vào (d),ta được:
\(2\left(2m-1\right)+3=1\)
=>2(2m-1)=-2
=>2m-1=-1
=>2m=0
=>m=0
Đúng 0
Bình luận (0)
giải hệ phương trình bằng phương pháp đặt ẩn phụ
Đọc tiếp
giải hệ phương trình bằng phương pháp đặt ẩn phụ
\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{3}{2}+\dfrac{1}{y}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{24}\end{matrix}\right.\) (Đk: x,y ≠ 0)
Đặt: \(\dfrac{1}{x}=u;\dfrac{1}{y}=v\)
Hệ trở thành:
\(\left\{{}\begin{matrix}u=\dfrac{3}{2}+v\\u+v=\dfrac{1}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{3}{2}+v\\\dfrac{3}{2}+v+v=\dfrac{1}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{3}{2}+v\\2v=-\dfrac{35}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{37}{48}\\v=-\dfrac{35}{48}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{37}{48}\\\dfrac{1}{y}=\dfrac{-35}{48}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{48}{37}\\y=-\dfrac{48}{35}\end{matrix}\right.\)
Vậy: \(\left(x;y\right)=\left(\dfrac{48}{37};-\dfrac{48}{35}\right)\)
Đúng 2
Bình luận (0)
Đổi \(6mm=0,006\left(m\right)\)
a.
Do ở nhiệt độ 40 độ C thanh có chiều dài 5m nên:
\(5=40a+b\) (1)
Ở nhiệt độ 140 độ thì chiều dài thanh là: \(5+0,006=5,006\left(m\right)\)
\(\Rightarrow5,006=140a+b\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}40a+b=5\\140a+b=5,006\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=0,00006\\b=4,9976\end{matrix}\right.\)
b.
Từ câu a ta có \(y=0,00006x+4,9976\)
Nên chiều dài thanh kim loại ở 100 độ là:
\(y=0,00006.100+4,9976=5,0036\left(m\right)\)
Đúng 1
Bình luận (0)
Vật kính của một máy ảnh có tiêu cự f=10cma. Vât cách máy 60cm. Phim phải đặt ở đâub. Phim chỉ dịch chuyển trong đoạn cách vật kính từ 10 đến 12,5cm. Hỏi máy ảnh có thể chụp được các vật cách máy ảnh một khoảng bao nhiêu
Vẽ hình thôi ạ
Xem chi tiết
Vẽ hình thôi ạ
Gọi số học sinh của lớp chuyên Văn là x (x nguyên dương và \(x< 75\))
Do 2 lớp có tổng cộng 75 học sinh nên số học sinh của lớp chuyên Sử là: \(75-x\)
Số học sinh của lớp chuyên Văn sau khi chuyển đi 15 em là: \(x-15\)
Số học sinh của lớp chuyên Sử sau khi nhận thêm 15 em là:
\(75-x+15=90-x\)
Do khi đó số học sinh chuyên Sử bằng 8/7 số học sinh chuyên Văn nên ta có pt:
\(90-x=\dfrac{8}{7}\left(x-15\right)\)
\(\Leftrightarrow630-7x=8x-120\)
\(\Leftrightarrow15x=750\)
\(\Leftrightarrow x=50\)
Vậy lớp chuyên Văn có 50 học sinh và chuyên Sử có 25 học sinh
Đúng 1
Bình luận (0)
2:
Thay x=1 và y=2 vào hệ phương trình, ta được:
2*2-a*2=b và a*1+b*2=1
=>-2a-b=-4 và a+2b=1
=>a=7/3 và b=-2/3
3:
Gọi chiều dài, chiều rộng lần lượt là a,b
Nửa chu vi là 216/2=108
Theo đề, ta có hệ phương trình:
a+b=108 và 0,8a+1,25b=a+b
=>a+b=108 và -0,2a=-0,25b
=>a+b=108 và 0,2a-0,25b=0
=>a=60 và b=48
Đúng 1
Bình luận (0)


















