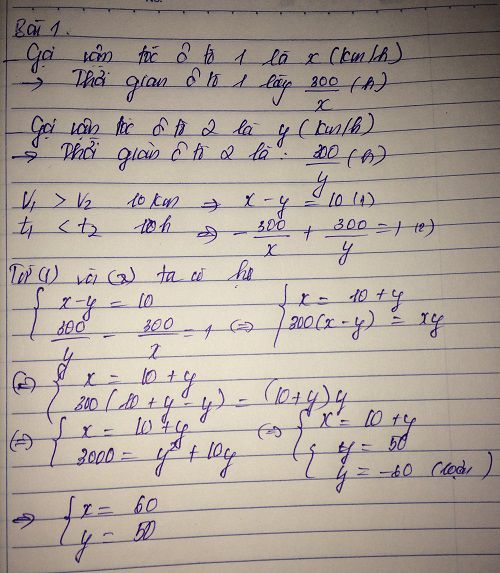Một người đi bộ từ A đến B dài 100km. Lúc về người đó chọn con đường khác để đi dài hơn con đường cũ 20km, vì đi với vận tốc lớn hơn 5km/h nhưng thời gian về vẫn nhiều hơn thời gian đi là 10 phút. tính vận đi.
Bài 6: Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)
Hai ô tô khởi hành cùng một lúc từ A đến B cách nhau 300km.Ô tô thứ nhất mỗi giờ chạy nhanh hơn ô tô thứ hai 1 giờ.Tính vận tốc mỗi xe ô tô
Một lớp có 40 học sinh được xếp ngồi cạnh nhau trên các ghế băng.Nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh .Tính số ghế băng lúc đầu
Gọi số ghế băng ban đầu là x(ghế)(x thuộc N*).
số học sinh/ghế là 40/x(học sinh).
số ghế khi bớt đi là : x-2(ghế)
số học sinh/ghế khi bớt ghế là : 40/x-2 (học sinh)
Do khi bớt đi 2 ghế ,số học sinh phải thêm 1 vào mỗi hàng nên ta có pt sau:
40/x-2 - 40/x = 1
<=>40x/x(x-2) - 40(x-2 ) /x(x-2) = x(x-2)/x(x-2)
==>40x - 40 (x-2) =x(x-2)
<=> 40x - 40x + 80 = x2 - 2x
<=> x2 - 2x - 80 = 0
Giải đenta ' ta có: đenta ' = (-1)2 - 1(-80)=1 + 80 = 81>0
==>Phương trình có hai nghiệm phân biệt
x1 =(-b' + 9)/a=(1 + 9 )/1=10.(thỏa mãn)
x2 =(-b' - 9)/a =( 1 - 9)/1 = -8(loại).
Vậy số ghế băng ban đầu là 10 ghế.
Đúng 0
Bình luận (0)
Cho đường tròn (O) và đường thẳng d không giao nhau với đường tròn (O).Gọi A là hình chiếu vuông góc của O trên đường thẳng d.Đường thẳng đi qua A (không đi qua O) cắt đường tròn (O) tại B và C (B nằm giữa A,C) .Tiếp tuyến tại B và C của đường tròn (O) cắt d lần lượt tại D và E.Đường thẳng BD cắt OA,CE lần lượt tại F và M,OE cắt AC ở N a) c/m tứ giác AOCE nội tiếp b) c/m AB.ENAF.EC...
Đọc tiếp
Cho đường tròn (O) và đường thẳng d không giao nhau với đường tròn (O).Gọi A là hình chiếu vuông góc của O trên đường thẳng d.Đường thẳng đi qua A (không đi qua O) cắt đường tròn (O) tại B và C (B nằm giữa A,C) .Tiếp tuyến tại B và C của đường tròn (O) cắt d lần lượt tại D và E.Đường thẳng BD cắt OA,CE lần lượt tại F và M,OE cắt AC ở N a) c/m tứ giác AOCE nội tiếp b) c/m AB.EN=AF.EC Giải giúp mk câu b.câu a bình thườg oy.cảm ơn các bạn!!!❤️
Một hình chữ nhật có đường chéo là 17m , biết chiều dài hơn chiều rộng là 7m. Tìm chiều dài , chiều rộng của hình chữ nhật.
Gọi chiều rộng của hcn là x (x\(\ge0\)) (m) Chiều rộng của hcn là x+7 (m) Do đường chéo của hcn dài 17m nên ta có pt: x2 + (x+7)2=172 ( Py-ta-go) <=> 2x2+14x-240=0 <=> x2+7x-120=0 <=> (x-8)(x+15)=0 <=> x=8 ( Do x>0) => chiều rộng của hcn là 8m, chiều dài của hcn là : 8+7=15 (m) Vậy .....
Đúng 0
Bình luận (0)
Để chở hết 1 số hàng có thể dùng thuyền lớn trở 4 chuyến hoặc dùng thuyền bé trở 6 chuyến. Thuyền lớn chỉ chở 1 số chuyến rồi làm việc khác, thuyền nhỏ làm tiếp cho xong. Như vậy 2 thuyền chở tổng cộng 5 chuyến Hỏi mỗi thuyền chở bao nhiêu chuyến ???
Một khu vườn hình chữ nhật có chu vi là 46 mét,nếu tăng chiều dài 5 mét và giảm chiều rộng 3 mét thì chiều dài gấp 4 lần chiều rộng. Hỏi kích thước khu vườn đó là bao nhiêu
Gọi x(m) là chiều dài hình chữ nhật
Gọi y(m) là chiều dài hình chữ nhật
ĐK: x>y; y>3
Chu vi của mảnh vườn hình chữ nhật là:
\((x+y).2=46 \) hay \(x+y=23(1)\)
Khi tăng chiều dài 5m : x+5(m)
Khi giảm chiều rộng 3m : y-3(m)
Thì chiều dài gấp 4 lần chiều rộng ta có:
\(x+5=4(y-3)\) hay \(x-4y=7(2)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=23\\x-4y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=23\\5y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=23\\y=\dfrac{16}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{16}{5}=23\\y=\dfrac{16}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{99}{5}\left(TM\right)\\y=\dfrac{16}{5}\left(TM\right)\end{matrix}\right.\)
Vậy chiều dài của mảnh vườn là \(\dfrac{99}{5}\)(m) và chiều rộng của mảnh vườn là \(\dfrac{16}{5}\)(m)
Đúng 0
Bình luận (0)
Một khu vườn HCN có chu vi 450m.Nếu ta giảm chiều dài đi 1/5 so với chiều dài cũ và tăng chiều rộng thêm 1/4 so với chiều rộng cũ thì chu vi HCN không đổi.Tính chiều dài và chiều rộng của khu vườn.
Nhờ các bạn chỉ cho mình bài này nha? Cám ơn các bạn
Gọi chiều dài là x (mét ,x>0)
=> Chu vi hcn là: 450 => nửa chu vi là: 225 => chiều rộng là: 225-y mét
chiều dài mới là: \(\frac{4x}{5}\) mét, chiều rộng mới là: \(\frac{5\left(225-x\right)}{4}\) mét
Chu vi mới không đổi nên: \(\frac{4x}{5}+\frac{5\left(225-x\right)}{4}=225\) <=> x=125
Vậy chiều rộng là: 225-125=100
Đúng 0
Bình luận (0)
Câu 1: a) Cho biết a2+sqrt{3} và b2-sqrt{3} .Tính giá trị biểu thức :Pa+b-ab
b) Giải hệ phương trình: left{{}begin{matrix}3x+y5x-2y-3end{matrix}right.
Câu 2: Cho biểu thức Pleft(dfrac{1}{x-sqrt{x}}+dfrac{1}{sqrt{x}-1}right):dfrac{sqrt{x}}{x-2sqrt{x}+1} (với xo,xne
a) Rút gọn biểu thức P
b) Tìm các giá trị của x để Pdfrac{1}{2}
Câu 3: Cho phương trình: x2-5x+m0 (m là tham số)
a) Giải phương trình khi m6...
Đọc tiếp
Câu 1: a) Cho biết a=2+\(\sqrt{3}\) và b=2-\(\sqrt{3}\) .Tính giá trị biểu thức :P=a+b-ab
b) Giải hệ phương trình: \(\left\{{}\begin{matrix}3x+y=5\\x-2y=-3\end{matrix}\right.\)
Câu 2: Cho biểu thức P=\(\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}\) (với x>o,x\(\ne\)
a) Rút gọn biểu thức P
b) Tìm các giá trị của x để P>\(\dfrac{1}{2}\)
Câu 3: Cho phương trình: x2-5x+m=0 (m là tham số)
a) Giải phương trình khi m=6
b) Tìm m để phương trình trên có nghiệm x1,x2 thỏa mãn:|x1-x2|=3
Câu 4: Cho đường tròn tâm O đường kính AB.Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O) .Lấy điểm E trên cung nhỏ BC (E khác B và C) ,AE cắt CD tại F .Chứng minh:
a) BEFI là tứ giác nội tiếp đường tròn
b) AE.AF=AC2
c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp \(\Delta\)CEF luôn thuộc một đường thẳng cố định
Câu 5: Cho hai số dương a,b thỏa mãn : a+b\(\le\) \(2\sqrt{2}\). .Tìm giá trị nhỏ nhất của biểu thức : P=\(\dfrac{1}{a}+\dfrac{1}{b}\)
Câu 1:
a, \(P=a+b-a.b\\ < =>P=2+\sqrt{3}+2-\sqrt{3}-\left(2+\sqrt{3}\right).\left(2-\sqrt{3}\right)\\ < =>P=4-\left(4-2\sqrt{3}+2\sqrt{3}-3\right)\\ < =>P=4-4+2\sqrt{3}-2\sqrt{3}+3\\ P=3\)
b, Gỉai hptrình:
\(\left\{{}\begin{matrix}3x+5=5\\x-2y=-3\end{matrix}\right.\)
Giaỉ hpt là tìm: x= 1; y=2
Đúng 0
Bình luận (0)
Câu 1b/ ta có: \(\left\{{}\begin{matrix}3x+y=5\\x-2y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(-3+2y\right)+y=5\\x-2y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y-9=5\\x-2y=-3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x-2y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
câu 2:
ta có:
\(P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{x-2\sqrt{x}+1}\)
\(P=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\)
\(P=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}\)
\(P=\dfrac{x-1}{x}\)
câu 5; ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\ge\dfrac{4}{2\sqrt{2}}=\sqrt{2}\)
Đúng 0
Bình luận (0)
5) Áp dụng BĐT Cô-si,ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}\) \(\geq\) \(\dfrac{4}{a+b}\) \(\geq\) \(\dfrac{4}{2\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow\) MinP=\(\sqrt{2}\) khi a=b=\(\sqrt{2}\)
Đúng 0
Bình luận (0)
các bạn giải giùm mình bài này( một người đi từ A>B trong một giờ lúc trở về đi được 1/3 quãng đường với vận tốc lớn hơn vận tốc lúc đi là 2km/h, phần đường còn lại người đó đi với vận tốc nhỏ hơn lúc đi là 1km/h nên lúc về chậm hơn lúc đi là 40s. Tính đoạn đường AB.cảm ơn trước