a) 2x - 3 > 3(x - 2)

⇔ 2x - 3 > 3x - 6

⇔ 2x - 3x > -6 + 3

⇔ -x > -3

⇔ x < 3

Vậy S = {x | x < 3}

b) (12x + 1)/12 ≤ (9x + 1)/3 - (8x + 1)/4

⇔ 12x + 1 ≤ 4(9x + 1) - 3(8x + 1)

⇔ 12x + 1 ≤ 36x + 4 - 24x - 3

⇔ 12x - 36x + 24x ≤ 4 - 3 - 1

⇔ 0x ≤ 0 (luôn đúng với mọi x)

Vậy S = R

a: =>2x-3>3x-6

=>-x>-3

=>x<3

b: =>12x+1<=36x+4-24x-3

=>12x+1<=12x+1

=>0x<=0(luôn đúng)

a) \(2x-3>3\left(x-2\right)\)

\(\Leftrightarrow2x-3>3x-6\)

\(\Leftrightarrow2x-3x>-6+3\)

\(\Leftrightarrow-x>-3\)

\(\Leftrightarrow x< 3\)

Vậy bất phương trình có nghiệm là \(x< 3\)

b) \(\dfrac{12x+1}{12}\le\dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)

\(\Leftrightarrow\dfrac{12x+1}{12}\le\dfrac{\left(9x+1\right).4}{3.4}-\dfrac{\left(8x+1\right)3}{4.3}\)

\(\Leftrightarrow12x+1\le36x+4-24x-3\)

\(\Leftrightarrow12x-36x+24x\le4-3-1\)

\(\Leftrightarrow0x\le0\)

Vậy bất phương trình vô nghiệm

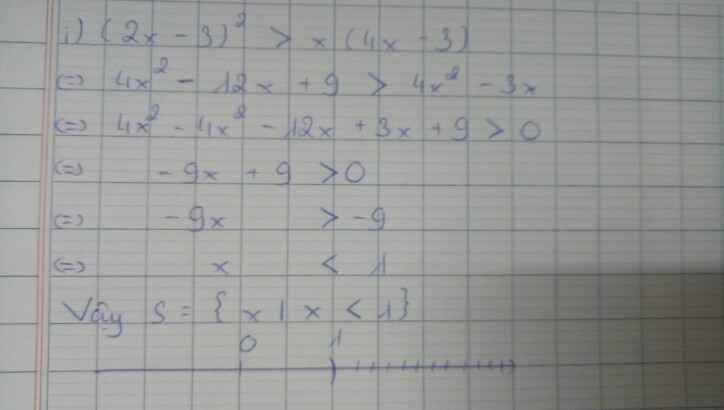
Ở câu (h) mình quên gạch chân phân số, bạn thông cảm nha <3

g: =>12x+1>=36x+12-24x-3

=>12x+1>=12x+9(loại)

h: =>6(x-1)+4(2-x)<=3(3x-3)

=>6x-6+8-4x<=9x-9

=>2x+2<=9x-9

=>-7x<=-11

=>x>=11/7

i: =>4x^2-12x+9>4x^2-3x

=>-12x+9>-3x

=>-9x>-9

=>x<1

\(\dfrac{12x+1}{12}\le\dfrac{4\left(9x+1\right)}{12}-\dfrac{3\left(8x+1\right)}{12}\)

\(\Leftrightarrow\)\(12x+1\le45x+4-32x+3\)

\(\Leftrightarrow12x+1\le13x+7\)

\(\Leftrightarrow12x-13x\le7-1\)

\(\Leftrightarrow-x\le6\)

\(\Leftrightarrow x\ge-6\)

mk nghĩ thế không bts đúng ko

a: =>4x^2-4x+1+7>4x^2+3x+1

=>-4x+8>3x+1

=>-7x>-7

=>x<1

b: \(\Leftrightarrow12x+1>=36x+12-24x-3\)

=>1>=9(loại)

24: 

\(\Leftrightarrow\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+\dfrac{1}{\left(x+4\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+6\right)}=\dfrac{1}{8}\)

\(\Leftrightarrow\dfrac{1}{x+2}-\dfrac{1}{x+6}=\dfrac{1}{8}\)

\(\Leftrightarrow\left(x+2\right)\left(x+6\right)=8\left(x+6\right)-8\left(x+2\right)\)

\(\Leftrightarrow x^2+8x+12=8x+48-8x-16=32\)

=>(x+10)(x-2)=0

=>x=-10 hoặc x=2

25: \(\Leftrightarrow\dfrac{\left(x+1\right)^2+1}{x+1}+\dfrac{\left(x+4\right)^2+4}{x+4}=\dfrac{\left(x+2\right)^2+2}{x+2}+\dfrac{\left(x+3\right)^2+3}{x+3}\)

\(\Leftrightarrow x+1+\dfrac{1}{x+1}+x+4+\dfrac{4}{x+4}=x+2+\dfrac{2}{x+2}+x+3+\dfrac{3}{x+3}\)

\(\Leftrightarrow\dfrac{1}{x+1}+\dfrac{4}{x+4}=\dfrac{2}{x+2}+\dfrac{3}{x+3}\)

\(\Leftrightarrow x+5=0\)

hay x=-5

d: \(\Leftrightarrow\dfrac{\left(x+2\right)^2}{\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{A}\)

hay A=x-2

1.

\(x^4-6x^2-12x-8=0\)

\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)

\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)

\(\Leftrightarrow x=1\pm\sqrt{5}\)

3.

ĐK: \(x\ge-9\)

\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)

\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)

\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)

Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)

\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)

\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)

\(\Leftrightarrow...\)

2.

ĐK: \(x\ne\dfrac{2\pm\sqrt{2}}{2};x\ne\dfrac{-2\pm\sqrt{2}}{2}\)

\(\dfrac{x}{2x^2+4x+1}+\dfrac{x}{2x^2-4x+1}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{1}{2x+\dfrac{1}{x}+4}+\dfrac{1}{2x+\dfrac{1}{x}-4}=\dfrac{3}{5}\)

Đặt \(2x+\dfrac{1}{x}+4=a;2x+\dfrac{1}{x}-4=b\left(a,b\ne0\right)\)

\(pt\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{5}\left(1\right)\)

Lại có \(a-b=8\Rightarrow a=b+8\), khi đó:

\(\left(1\right)\Leftrightarrow\dfrac{1}{b+8}+\dfrac{1}{b}=\dfrac{3}{5}\)

\(\Leftrightarrow\dfrac{2b+8}{\left(b+8\right)b}=\dfrac{3}{5}\)

\(\Leftrightarrow10b+40=3\left(b+8\right)b\)

\(\Leftrightarrow\left[{}\begin{matrix}b=2\\b=-\dfrac{20}{3}\end{matrix}\right.\)

TH1: \(b=2\Leftrightarrow...\)

TH2: \(b=-\dfrac{20}{3}\Leftrightarrow...\)

1) \(\dfrac{1}{27}+a^3=\left(\dfrac{1}{3}+a\right)\left(\dfrac{1}{9}-\dfrac{a}{3}+a^2\right)\)

2) \(=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)\)

3) \(=\left(\dfrac{1}{2}x+2y\right)\left(\dfrac{1}{4}x-xy+4y^2\right)\)

4) \(=\left(x^2+1\right)\left(x^4-x^2+1\right)\)

5) \(=\left(x^3+1\right)\left(x^6-x^3+1\right)\)

6) \(=\left(x-4\right)\left(x^2+4x+16\right)\)

7) \(=\left(x-5\right)\left(x^2+5x+25\right)\)

8) \(=\left(2x^2-3y\right)\left(4x^4+6x^2y+9y^2\right)\)

9) \(=\left(\dfrac{1}{4}x^2-5y\right)\left(\dfrac{1}{16}x^4+\dfrac{5}{4}x^2y+25y^2\right)\)

10) \(=\left(\dfrac{1}{2}x-2\right)\left(\dfrac{1}{4}x^2+x+4\right)\)

11) \(=\left(x+2\right)^3\)

12) \(=\left(x+3\right)^3\)