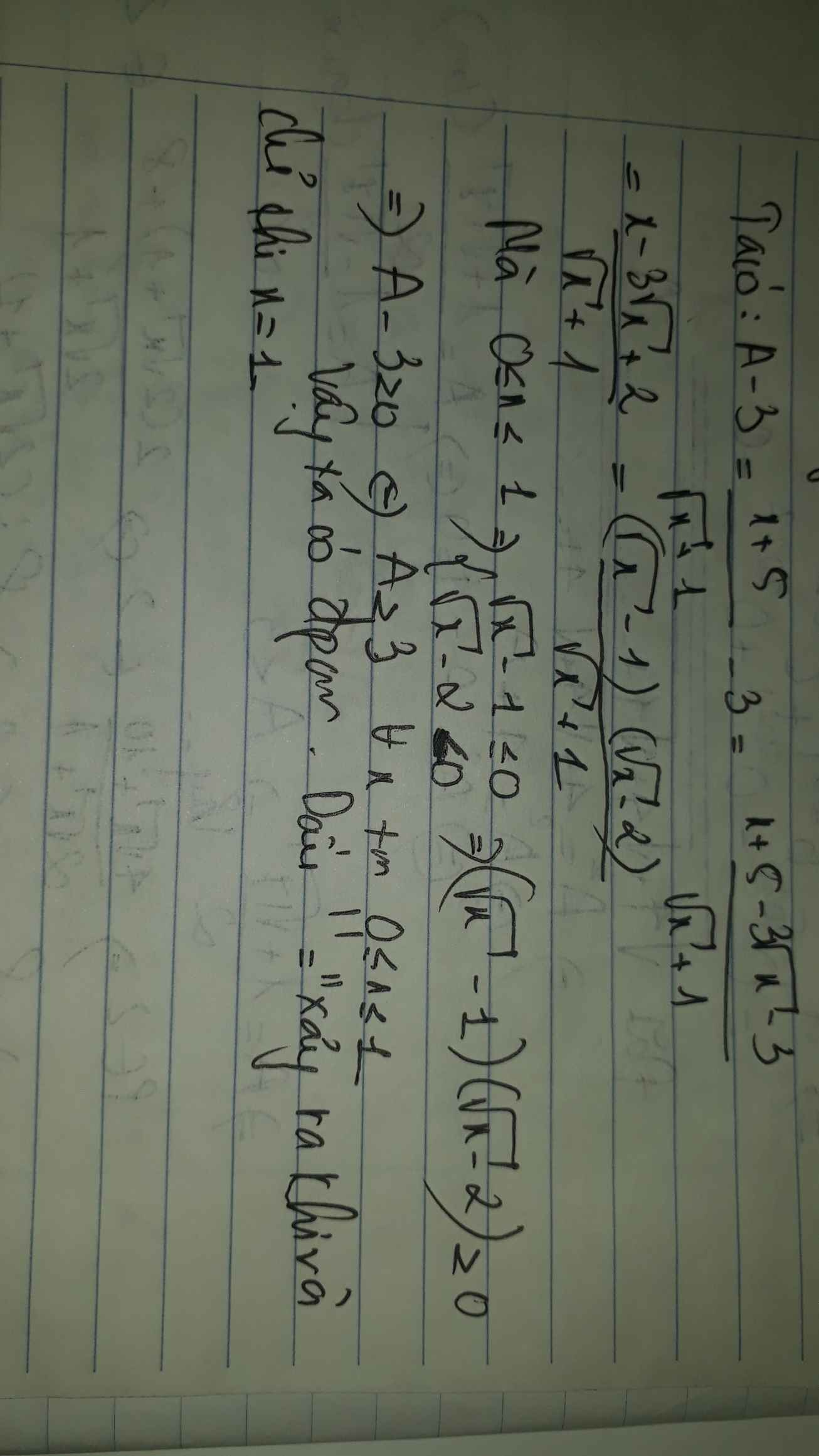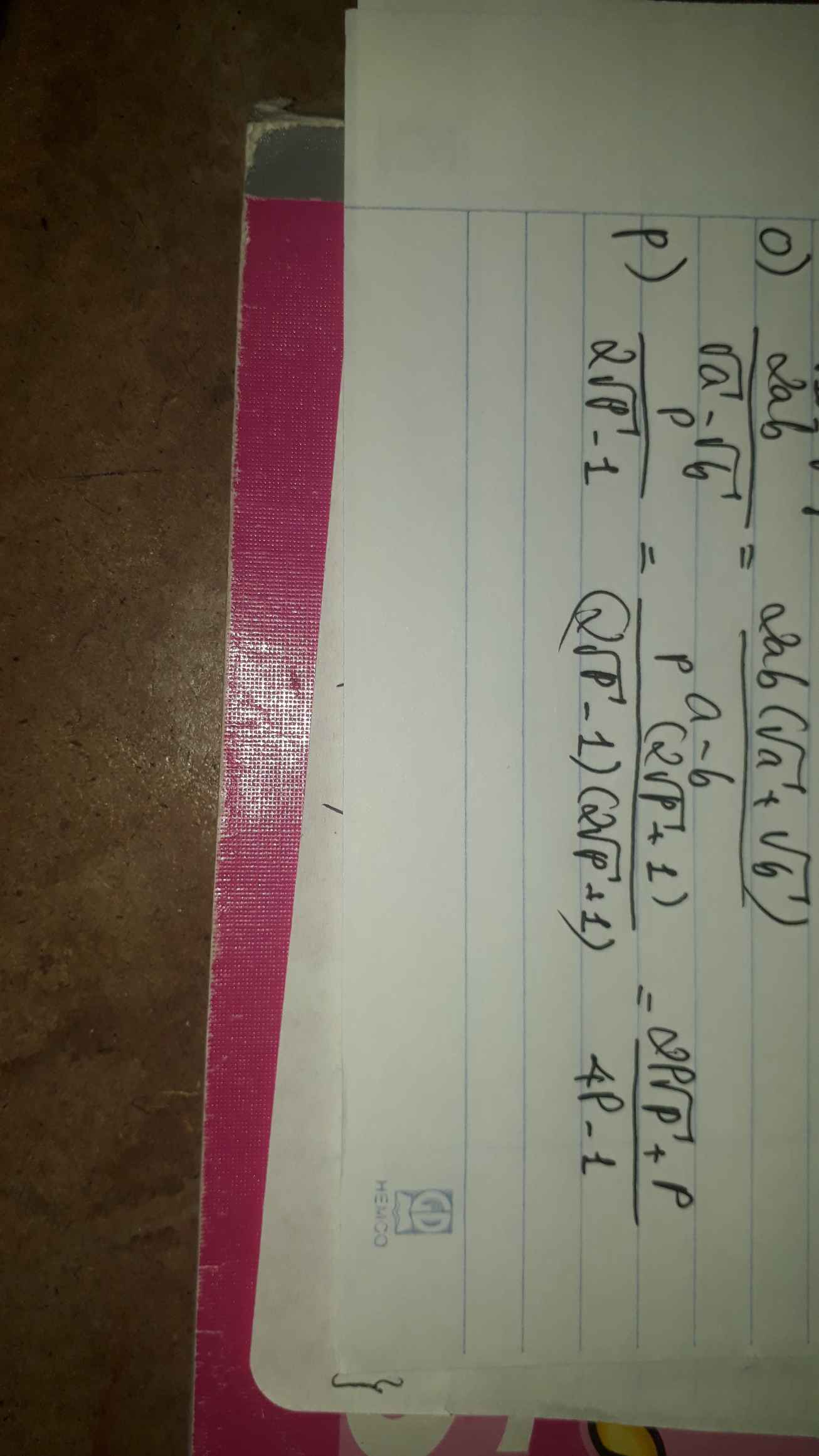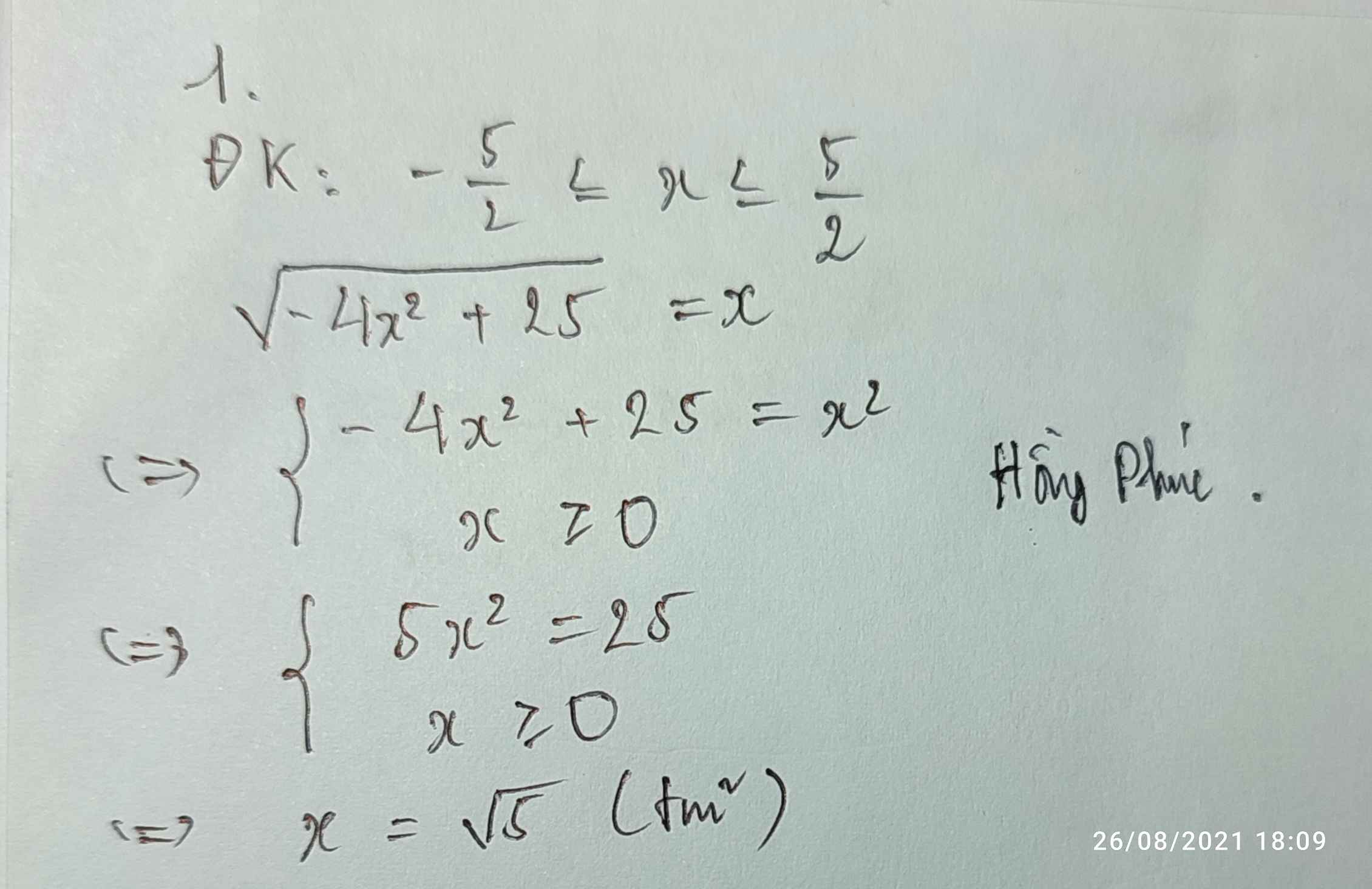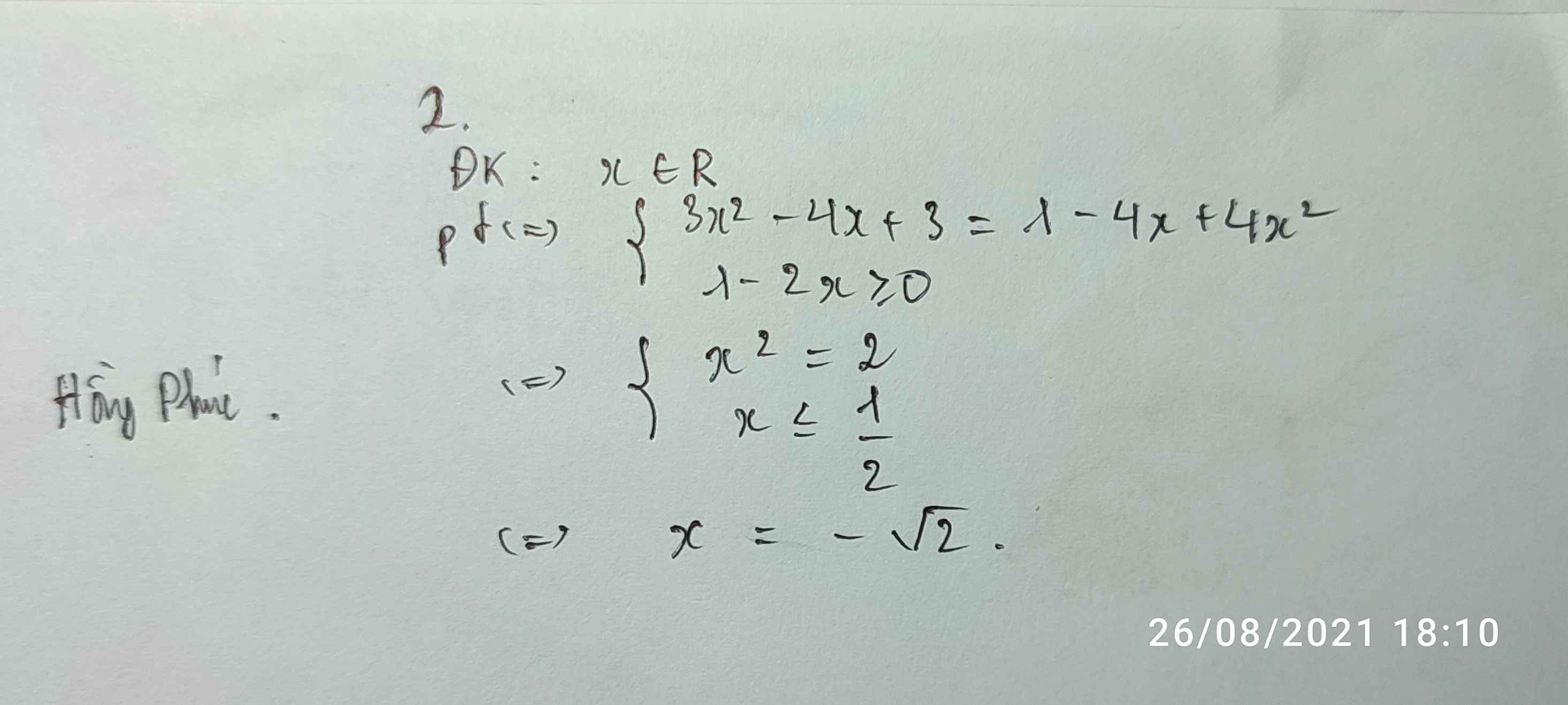\(\sqrt{48\cdot45}=12\sqrt{15}\\ \sqrt{225\cdot17}=15\sqrt{17}\\ \sqrt{a^3b^7}=\left|ab^3\right|\sqrt{ab}=ab^3\sqrt{ab}\\ \sqrt{x^5\left(x-3\right)^2}=\left|x^2\left(x-3\right)\right|\sqrt{x}=x^2\left(x-3\right)\sqrt{x}\)

\(\sqrt{48\cdot45}=4\sqrt{3}\cdot3\sqrt{5}=12\sqrt{15}\)

\(\sqrt{225\cdot17}=15\sqrt{17}\)

Ta có: \(A-3\)

\(=\dfrac{x+5-3\sqrt{x}-3}{\sqrt{x}+1}\)

\(=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}+1}\ge0\forall x\) thỏa mãn ĐKXĐ

hay A\(\ge3\)

Câu 1 :

a, Ta có : \(A=x-2\sqrt{3}+3\)

\(=x-\sqrt{3}\left(2-\sqrt{3}\right)\)

\(=\left(\sqrt{x}-\sqrt{\sqrt{3}\left(2-\sqrt{3}\right)}\right)\left(\sqrt{x}+\sqrt{\sqrt{3}\left(2-\sqrt{3}\right)}\right)\)

b, Ta có : \(B=x+2\sqrt{x}-3\)

\(=x+2\sqrt{x}+1-4=\left(\sqrt{x}+1\right)^2-4\)

\(=\left(\sqrt{x}+1-2\right)\left(\sqrt{x}+1+2\right)=\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)\)

c, Ta có : \(C=x\sqrt{x}-1\)

\(=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)

d, Ta có : \(D=2x-3\sqrt{xy}-5y\)

\(=2x+2\sqrt{xy}-5\sqrt{xy}-5y\)

\(=2\sqrt{x}\left(\sqrt{x}+\sqrt{y}\right)-5\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)\)

\(=\left(\sqrt{x}+\sqrt{y}\right)\left(2\sqrt{x}-5\sqrt{y}\right)\)

f: \(\dfrac{2}{\sqrt{6}-\sqrt{5}}=2\sqrt{6}+2\sqrt{5}\)

l: \(\dfrac{3}{\sqrt{10}+\sqrt{7}}=\sqrt{10}-\sqrt{7}\)

m: \(\dfrac{1}{\sqrt{x}-\sqrt{y}}=\dfrac{\sqrt{x}+\sqrt{y}}{x-y}\)

a) ta có : \(\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\sqrt{x}-\sqrt{y}}=x+\sqrt{xy}+y\)

b) ta có : \(\dfrac{x-\sqrt{3x}+3}{x\sqrt{x}+3\sqrt{3}}=\dfrac{x-\sqrt{3x}+3}{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{3x}+3\right)}=\dfrac{1}{\sqrt{x}+\sqrt{y}}\)

\(T=\sqrt{\dfrac{3\sqrt{x}}{\sqrt{x}-6}\cdot\dfrac{x-6\sqrt{x}}{\sqrt{x}-1}}=\sqrt{\dfrac{3\sqrt{x}}{\sqrt{x}-6}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-6\right)}{\sqrt{x}-1}}\\ =\sqrt{\dfrac{3\sqrt{x}\cdot\sqrt{x}}{\sqrt{x}-1}}=\sqrt{\dfrac{3x}{\sqrt{x}-1}}\\ =\sqrt{\dfrac{3\left(x-1\right)+3}{\sqrt{x}-1}}=\sqrt{3\left(\sqrt{x}+1\right)+\dfrac{3}{\sqrt{x}-1}}\\ =\sqrt{3\left(\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}\right)+6}\)

Áp dụng bất đẳng thức Cosi ta có:

\(\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}\ge2\)

\(\Rightarrow T\ge\sqrt{3\cdot2+6}=2\sqrt{3}\)

Dấu = xảy ra khi x=4

\(a.\sqrt{32+10\sqrt{7}}+\sqrt{32-10\sqrt{7}}=\sqrt{25+2.5\sqrt{7}+7}+\sqrt{25-2.5\sqrt{7}+7}=5+\sqrt{7}+5-\sqrt{7}=10\)

\(b.\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}=\sqrt{13+30\sqrt{2+\sqrt{8+2.2\sqrt{2}+1}}}=\sqrt{13+30\sqrt{2+2\sqrt{2}+1}}=\sqrt{13+30\left(\sqrt{2}+1\right)}=\sqrt{25+2.5.3\sqrt{2}+18}=5+3\sqrt{2}\) \(c.\dfrac{3-\sqrt{x}}{9-x}=\dfrac{3-\sqrt{x}}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}=\dfrac{1}{3+\sqrt{x}}\)

\(d.\dfrac{x-5\sqrt{x}+6}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}{\sqrt{x}-3}=\sqrt{x}-2\)

\(e.\dfrac{x-3\sqrt{x}+2}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-1}=\sqrt{x}-2\)

\(f.\dfrac{x\sqrt{x}+64}{\sqrt{x}+4}=\dfrac{\left(\sqrt{x}+4\right)\left(x-4\sqrt{x}+16\right)}{\sqrt{x}+4}=x-4\sqrt{x}+16\)

\(g.\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\sqrt{x}-\sqrt{y}}=x+\sqrt{xy}+y\)

Còn 2 con cuối làm tương tự nhé ( đăng dài quá ).

\(a.\sqrt{32+10\sqrt{7}}+\sqrt{32-10\sqrt{7}}=\sqrt{25+2.\sqrt{25}.\sqrt{7}+7}+\sqrt{25-2.\sqrt{25}.\sqrt{7}+7}=\sqrt{\left(5+\sqrt{7}\right)^2}+\sqrt{\left(5-\sqrt{7}\right)^2}=5+\sqrt{7}+5-\sqrt{7}=10\)\(b.\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}=\sqrt{13+30\sqrt{2+\sqrt{8+2.\sqrt{8}.1}+1}}=\sqrt{13+30\sqrt{2+\sqrt{\left(\sqrt{8}+1\right)^2}}}=\sqrt{13+30\sqrt{2+\sqrt{8}+1}}=\sqrt{13+30\sqrt{3+2\sqrt{2}}=\sqrt{13+30\sqrt{\left(\sqrt{2}+1\right)^2}}}=\sqrt{13+30\sqrt{2}+30}=\sqrt{\sqrt{25}+2.\sqrt{25}.\sqrt{18}+18}=\sqrt{\left(5+\sqrt{18}\right)^2}=5+\sqrt{18}\)

\(c.\dfrac{3-\sqrt{x}}{9-x}=\dfrac{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}{9-x}.\dfrac{1}{3+\sqrt{x}}=\dfrac{9-x}{9-x}.\dfrac{1}{3+\sqrt{x}}=\dfrac{1}{3+\sqrt{x}}=\dfrac{3-\sqrt{x}}{9-x}\)\(d.\dfrac{x-5\sqrt{x}+6}{\sqrt{x}-3}=\dfrac{x-2\sqrt{x}-3\sqrt{x}+6}{\sqrt{x}-3}=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)}=\sqrt{x}-2\)\(e.\dfrac{x-3\sqrt{x}+2}{\sqrt{x}-1}=\dfrac{x-\sqrt{x}-2\sqrt{x}+2}{\sqrt{x}-1}=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-2\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-1}=\sqrt{x}-2\)

\(g.\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=\dfrac{\left(x\sqrt{x}-y\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{x^2+x\sqrt{xy}-y\sqrt{xy}-y^2}{x-y}=\dfrac{\sqrt{xy}\left(x-y\right)+\left(x-y\right)\left(x+y\right)}{x-y}=\dfrac{\left(x-y\right)\left(\sqrt{xy}+x+y\right)}{x-y}=x+y+\sqrt{xy}\)\(h.6-2x-\sqrt{9-6x+x^2}=6-2x-\sqrt{\left(x-3\right)^2}=6-2x-\left|x-3\right|=6-2x-3+x=3-x\)

\(i.\sqrt{x+2+2\sqrt{x+1}}=\sqrt{x+1+2\sqrt{x+1}+1}=\sqrt{\left(\sqrt{x+1}+1\right)^2}=\sqrt{x+1}+1\)

a) \(\sqrt{32+10\sqrt{7}}+\sqrt{32-10\sqrt{7}}\)

\(=\sqrt{\left(5+\sqrt{7}\right)^2}+\sqrt{\left(5-\sqrt{7}\right)^2}\)

\(=5+\sqrt{7}+5-\sqrt{7}\)

=10

b)\(\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}\)

\(=\sqrt{13+30\sqrt{2+\sqrt{\left(1+2\sqrt{2}\right)^2}}}\)

\(=\sqrt{13+30\sqrt{3+2\sqrt{2}}}\)

\(=\sqrt{13+30\sqrt{\left(\sqrt{2}+1\right)^2}}\)

\(=\sqrt{13+30\left(\sqrt{2}+1\right)}\)

\(=\sqrt{13+30\sqrt{2}+30}\)

\(=\sqrt{43+30\sqrt{2}}\)

\(=\sqrt{\left(5+3\sqrt{2}\right)^2}\)

\(=5+3\sqrt{2}\)