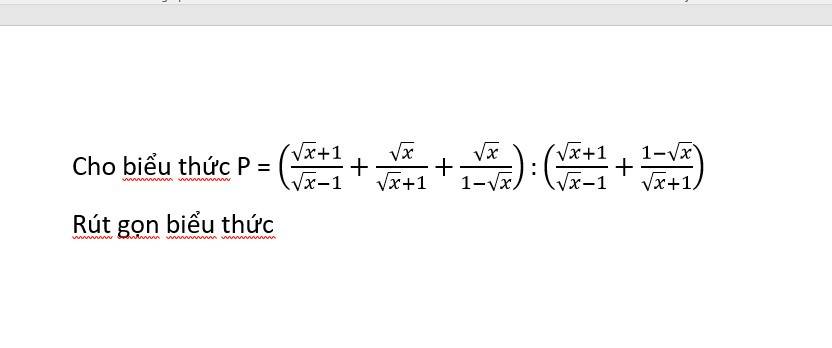Tính A= -2√3 (3-√3) + (3√3 +1)²
Bài 7: Biến đối đơn giản biểu thức chứa căn bậc hai (Tiếp theo)
\(A=-2\sqrt{3}\left(3-\sqrt{3}\right)+\left(3\sqrt{3}+1\right)^2\)
\(=-6\sqrt{3}+6+\left(3\sqrt{3}\right)^2+2\cdot3\sqrt{3}\cdot1+1^2\)
\(=-6\sqrt{3}+6+27+6\sqrt{3}+1\)
\(=34\)
Đúng 2
Bình luận (0)
căn 10 trừ căn 5 phần 3 trừ căn 18
\(\sqrt{10}-\sqrt{\dfrac{5}{3}}-\sqrt{18}\)
\(=\sqrt{10}-\dfrac{\sqrt{5}}{\sqrt{3}}-3\sqrt{2}\)
\(=\sqrt{10}-\dfrac{\sqrt{15}}{3}-3\sqrt{2}\)
\(=\dfrac{3\sqrt{10}-\sqrt{15}-9\sqrt{2}}{3}\)
Đúng 0
Bình luận (0)
GIÚP MÌNH VS Ạ='(( MÌNH CẢM ƠN NHÌU!!
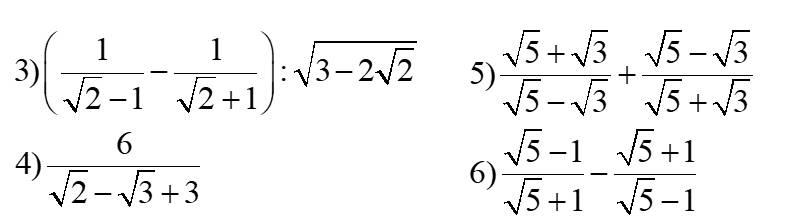
3: \(\left(\dfrac{1}{\sqrt{2}-1}-\dfrac{1}{\sqrt{2}+1}\right):\sqrt{3-2\sqrt{2}}\)
\(=\dfrac{\sqrt{2}+1-\sqrt{2}+1}{2-1}:\left(\sqrt{2}-1\right)\)
\(=\dfrac{2}{\sqrt{2}-1}=2\left(\sqrt{2}+1\right)=2\sqrt{2}+2\)
5:
\(\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}+\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
\(=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2+\left(\sqrt{5}-\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}\)
\(=\dfrac{8+2\sqrt{15}+8-2\sqrt{15}}{2}=\dfrac{16}{2}=8\)
6:
\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}-\dfrac{\sqrt{5}+1}{\sqrt{5}-1}\)
\(=\dfrac{\left(\sqrt{5}-1\right)^2-\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{6-2\sqrt{5}-6-2\sqrt{5}}{4}=\dfrac{-4\sqrt{5}}{4}=-\sqrt{5}\)
4:
\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{2}-\sqrt{3}+3\right)}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{5-2\sqrt{6}-9}=\dfrac{-6\left(\sqrt{2}-\sqrt{3}-3\right)}{4+2\sqrt{6}}\)
\(=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)}{\sqrt{6}+2}=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{6}-2\right)}{2}\)
\(=\dfrac{-3\left(2\sqrt{3}-2\sqrt{2}-3\sqrt{2}+2\sqrt{3}-6\sqrt{3}+6\right)}{2}\)
\(=\dfrac{-3\left(-2\sqrt{3}-5\sqrt{2}+6\right)}{2}\)
Đúng 1
Bình luận (0)
giải các phương trình :
a) \(\sqrt{-x^2+x+4}=x-3\)
b)\(\sqrt{-2x^2+6}=x-1\)
c) \(\sqrt{x+2}=1+\sqrt{x-3}\)
a) \(\sqrt{-x^2+x+4}=x-3\left(đk:x\ge3\right)\)
\(-x^2+x+4=x^2-6x+9\)
\(2x^2-7x-5=0\)
\(\Delta=49-4.2.\left(-5\right)=89\)
\(\left[{}\begin{matrix}x=\dfrac{7+\sqrt{89}}{4}\left(TM\right)\\x=\dfrac{7-\sqrt{89}}{4}\left(L\right)\end{matrix}\right.\)
b) \(\sqrt{-2x^2+6}=x-1\left(đk:x\ge1\right)\)
\(-2x^2+6=x^2-2x+1\)
\(3x^2-2x-5=0\)
\(\Delta=4+4.3.5=64\)
\(\left[{}\begin{matrix}x=\dfrac{2-8}{6}=-1\left(L\right)\\x=\dfrac{2+8}{6}=\dfrac{5}{3}\left(TM\right)\end{matrix}\right.\)
c) \(\sqrt{x+2}=1+\sqrt{x-3}\left(Đk:x\ge3\right)\)
\(x+2=1+x-3+2\sqrt{x-3}\)
\(\sqrt{x-3}=2\)
\(x-3=4\)
\(x=7\)
Đúng 2
Bình luận (0)
chứng minh :a) 11+6sqrt{2} (3+sqrt{2})^2 b) sqrt{11+6sqrt{2}}+sqrt{11-6sqrt{2}}6 c) sqrt{8-2sqrt{7}}-sqrt{8+2sqrt{7}} -2 d) sqrt{49-12sqrt{5}}-sqrt{49+12sqrt{5}}-4
Đọc tiếp
chứng minh :a) 11+6\(\sqrt{2}\)= (3+\(\sqrt{2}\))\(^2\)
b) \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)=6
c) \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)= -2
d) \(\sqrt{49-12\sqrt{5}}-\sqrt{49+12\sqrt{5}}\)=-4
a: \(\left(3+\sqrt{2}\right)^2=3^2+2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2\)
\(=9+6\sqrt{2}+2=11+6\sqrt{2}\)
b: \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=3+\sqrt{2}+3-\sqrt{2}=6\)
c: \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
d: \(\sqrt{49-12\sqrt{5}}-\sqrt{49+12\sqrt{5}}\)
\(=\sqrt{45-2\cdot3\sqrt{5}\cdot2+4}-\sqrt{45+2\cdot3\sqrt{5}\cdot2+4}\)
\(=\sqrt{\left(3\sqrt{5}-2\right)^2}-\sqrt{\left(3\sqrt{5}+2\right)^2}\)
\(=3\sqrt{5}-2-3\sqrt{5}-2=-4\)
Đúng 3
Bình luận (0)
a) \(\left(3+\sqrt{2}\right)^2=9+6\sqrt{2}+2=11+6\sqrt{2}\)
b) \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=3+\sqrt{2}+3-\sqrt{2}=6\)
c) \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
d) \(\sqrt{49-12\sqrt{5}}-\sqrt{49+12\sqrt{5}}\)
\(=\sqrt{\left(3\sqrt{5}-2\right)^2}-\sqrt{\left(3\sqrt{5}+2\right)^2}\)
\(=3\sqrt{5}-2-3\sqrt{5}-2=-4\)
Đúng 1
Bình luận (0)
Rút gọn các biểu thức :
a) \(\sqrt{\left(4-\sqrt{15}\right)^2}+\sqrt{15}\)
b) \(\sqrt{7+4\sqrt{3}}-\sqrt{7-4\sqrt{3}}\)
c)\(\sqrt{29+12\sqrt{5}}-\sqrt{29-12\sqrt{5}}\)
a: \(\sqrt{\left(4-\sqrt{15}\right)^2}+\sqrt{15}\)
\(=4-\sqrt{15}+\sqrt{15}=4\)
b: \(\sqrt{7+4\sqrt{3}}-\sqrt{7-4\sqrt{3}}\)
\(=2+\sqrt{3}-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: \(\sqrt{29+12\sqrt{5}}-\sqrt{29-12\sqrt{5}}\)
\(=\sqrt{\left(2\sqrt{5}+3\right)^2}-\sqrt{\left(2\sqrt{5}-3\right)^2}\)
\(=2\sqrt{5}+3-2\sqrt{5}+3=6\)
Đúng 2
Bình luận (0)
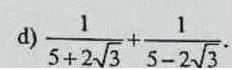 ghi rõ cách làm giùm em ạ
ghi rõ cách làm giùm em ạ
\(\dfrac{1}{5+2\sqrt{3}}+\dfrac{1}{5-2\sqrt{3}}\)
\(=\dfrac{5-2\sqrt{3}+5+2\sqrt{3}}{\left(5-2\sqrt{3}\right)\left(5+2\sqrt{3}\right)}\)
\(=\dfrac{10}{25-12}=\dfrac{10}{13}\)
Đúng 1
Bình luận (0)
\(\dfrac{1}{5+2\sqrt{3}}+\dfrac{1}{5-2\sqrt{3}}\\ =\dfrac{5-2\sqrt{3}}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}+\dfrac{5+2\sqrt{3}}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\\ =\dfrac{5-2\sqrt{3}+5+2\sqrt{3}}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\\ =\dfrac{10}{5^2-\left(2\sqrt{3}\right)^2}\\ =\dfrac{5+5}{25-12}=\dfrac{10}{13}\)
Đúng 1
Bình luận (0)
\(\dfrac{1}{5+2\sqrt{3}}+\dfrac{1}{5-2\sqrt{3}}\)
\(=\dfrac{1.\left(5-2\sqrt{3}\right)}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}+\dfrac{1.\left(5+2\sqrt{3}\right)}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\)
\(=\dfrac{5-2\sqrt{3}+5+2\sqrt{3}}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\)
\(=\dfrac{10}{25-12}=\dfrac{10}{13}\)
Đúng 0
Bình luận (0)
\(\sqrt{x+1}+\sqrt{x-2}=3\)
\(\sqrt{x+1}+\sqrt{x-2}=3\left(Đk:x\ge2\right)\)
\(x+1+x-2+2\sqrt{\left(x+1\right)\left(x-2\right)}=9\)
\(2\sqrt{x^2-2x+x-2}=10-2x\)
\(\sqrt{x^2-x-2}=5-x\)
\(x^2-x-2=x^2-2x+25\)
\(x=27\)
Đúng 2
Bình luận (0)
rút gọn
\(\dfrac{25}{x^2-y^2}\)\(\sqrt{\dfrac{x^22xy+y^2}{625}}\)
\(\dfrac{25}{x^2-y^2}\sqrt{\dfrac{x^2-2xy+y^2}{625}};x>y>0?\\ =\dfrac{25}{x^2-y^2}\sqrt{\dfrac{\left(x-y\right)^2}{625}}\\ =\dfrac{25}{x^2-y^2}\cdot\dfrac{\sqrt{\left(x-y\right)^2}}{\sqrt{625}}\\ =\dfrac{25}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{x-y}{25}\\ =\dfrac{1}{x+y}\)
Đúng 2
Bình luận (0)
\(P=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{1-\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\right)\left(ĐKXĐ:x>0;x\ne1\right)\\ P=\left(\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ P=\left(\dfrac{\sqrt{x}+1+\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{4\sqrt{x}}\\ P=\dfrac{x+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{4\sqrt{x}}\\ P=\dfrac{x+1}{4\sqrt{x}}\)
Đúng 1
Bình luận (0)