3: \(\left(\dfrac{1}{\sqrt{2}-1}-\dfrac{1}{\sqrt{2}+1}\right):\sqrt{3-2\sqrt{2}}\)
\(=\dfrac{\sqrt{2}+1-\sqrt{2}+1}{2-1}:\left(\sqrt{2}-1\right)\)
\(=\dfrac{2}{\sqrt{2}-1}=2\left(\sqrt{2}+1\right)=2\sqrt{2}+2\)
5:
\(\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}+\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
\(=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2+\left(\sqrt{5}-\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}\)
\(=\dfrac{8+2\sqrt{15}+8-2\sqrt{15}}{2}=\dfrac{16}{2}=8\)
6:
\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}-\dfrac{\sqrt{5}+1}{\sqrt{5}-1}\)
\(=\dfrac{\left(\sqrt{5}-1\right)^2-\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{6-2\sqrt{5}-6-2\sqrt{5}}{4}=\dfrac{-4\sqrt{5}}{4}=-\sqrt{5}\)
4:
\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{2}-\sqrt{3}+3\right)}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{5-2\sqrt{6}-9}=\dfrac{-6\left(\sqrt{2}-\sqrt{3}-3\right)}{4+2\sqrt{6}}\)
\(=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)}{\sqrt{6}+2}=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{6}-2\right)}{2}\)
\(=\dfrac{-3\left(2\sqrt{3}-2\sqrt{2}-3\sqrt{2}+2\sqrt{3}-6\sqrt{3}+6\right)}{2}\)
\(=\dfrac{-3\left(-2\sqrt{3}-5\sqrt{2}+6\right)}{2}\)

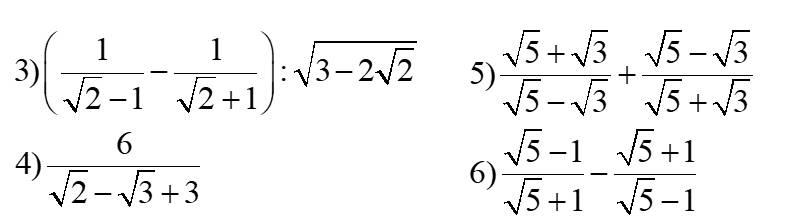




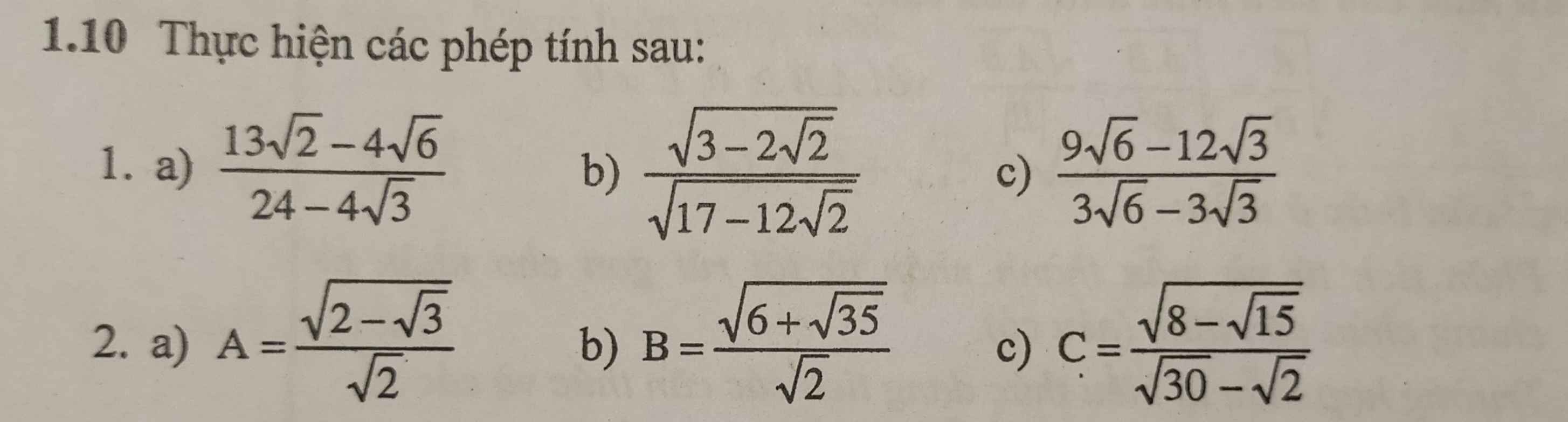





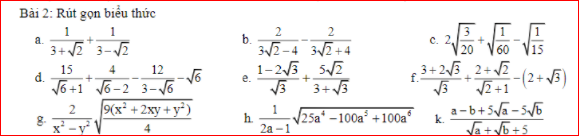

 giúp mình câu 11 , 12 v ạ mình camon
giúp mình câu 11 , 12 v ạ mình camon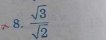 trục căn thức ở mẫu giúp mình v ạ mình camonn
trục căn thức ở mẫu giúp mình v ạ mình camonn

 trục căn thức ở mẫu giúp mình v ạ
trục căn thức ở mẫu giúp mình v ạ