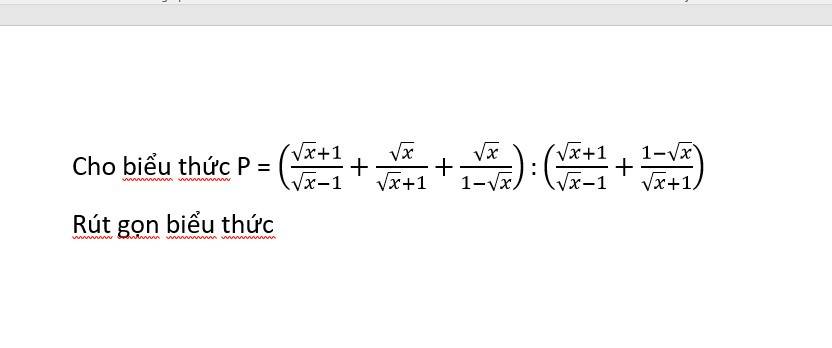\(P=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{1-\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\right)\left(ĐKXĐ:x>0;x\ne1\right)\\ P=\left(\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ P=\left(\dfrac{\sqrt{x}+1+\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{4\sqrt{x}}\\ P=\dfrac{x+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{4\sqrt{x}}\\ P=\dfrac{x+1}{4\sqrt{x}}\)
Bài 7: Biến đối đơn giản biểu thức chứa căn bậc hai (Tiếp theo)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Rút gọn các biểu thức sau : ( giá trị các biểu thức chứa chữ đều có nghĩa )
a, 5sqrt{frac{1}{5}} . frac{1}{2}sqrt{20} + sqrt{5}
b, sqrt{frac{1}{2}} + sqrt{4,5}
c, sqrt{20} + sqrt{45} - 3sqrt{75} + sqrt{72}
d, 5sqrt{a} - 4sqrt{25a^2} + sqrt{9a} - 2sqrt{16a}
e, frac{2+sqrt{3}}{sqrt{2}+sqrt{2+sqrt{3}}} + frac{2-sqrt{3}}{sqrt{2}-sqrt{2-sqrt{3}}}
g, frac{3+sqrt{5}}{sqrt{2}+sqrt{3+sqrt{5}}} + frac{3-sqrt{5}}{sqrt{2}-sqrt{3-sqrt{5}}}
Đọc tiếp
Rút gọn các biểu thức sau : ( giá trị các biểu thức chứa chữ đều có nghĩa )
a, \(5\sqrt{\frac{1}{5}}\) . \(\frac{1}{2}\sqrt{20}\) + \(\sqrt{5}\)
b, \(\sqrt{\frac{1}{2}}\) + \(\sqrt{4,5}\)
c, \(\sqrt{20}\) + \(\sqrt{45}\) - \(3\sqrt{75}\) + \(\sqrt{72}\)
d, \(5\sqrt{a}\) - \(4\sqrt{25a^2}\) + \(\sqrt{9a}\) - \(2\sqrt{16a}\)
e, \(\frac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}\) + \(\frac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
g, \(\frac{3+\sqrt{5}}{\sqrt{2}+\sqrt{3+\sqrt{5}}}\) + \(\frac{3-\sqrt{5}}{\sqrt{2}-\sqrt{3-\sqrt{5}}}\)
1. Giải phương trình: \(\sqrt{\left(4+x\right)\left(6-x\right)}=x^2-2x-12\)
2. Giải phương trình: \(3\left(x^2-6\right)=8\left(\sqrt{x^3-1}-3\right)\)
B=\(\left(\dfrac{3}{\sqrt{1+a}}+\sqrt{1-a}\right):\left(\dfrac{3}{\sqrt{1-a^2}}+1\right)\)
a) Rút gọn
b) Tìm B khi a=\(\dfrac{\sqrt{3}}{2+\sqrt{3}}\)
c) Tìm a để \(\sqrt{B}>B\)
Tìm Min và Max(nếu có)
A=2x-\(\sqrt{x}\)
B=x+\(\sqrt{x}\)
C=1+\(\sqrt{2-x}\)
D=\(\sqrt{-x^2+2x+5}\)
E=\(\dfrac{1}{2x-\sqrt{x}+3}\)
F=\(\dfrac{1}{3-\sqrt{1-x^2}}\)
rút gọn
B=\(\dfrac{x\sqrt{x}-8}{x-2\sqrt{x}}-\dfrac{x\sqrt{x}+8}{x+2\sqrt{x}}+\dfrac{x+2}{\sqrt{x}}\)tìm đk để B rút gọn
C=\(\dfrac{1}{\sqrt{x}+2}-\dfrac{5}{x-\sqrt{x}-6}-\dfrac{\sqrt{x}-2}{3-\sqrt{x}}\)tìm x ∈Z để C ∈Z
Tính giá trị các biểu thức sau:
a. \(\sqrt{2-\sqrt{3}}.\left(\sqrt{6}+\sqrt{2}\right)\)
b. \(\left(\sqrt{21}+7\right).\sqrt{10-2\sqrt{21}}\)
rút gọn
A=\(\dfrac{8+x\left(1+\sqrt{x-2\sqrt{x}+1}\right)}{\left(x-4\right)\left(x-2\sqrt{x}+4\right)}+\dfrac{x-3\sqrt{x}}{2\left(x-\sqrt{x}-6\right)}\)
lm nhanh giúp mk nhé
Tính giá trị biểu thức (Nhân thêm số căn vào biểu thức để làm xuất hiện hằng đẳng thức \(\left(a\pm\sqrt{b}\right)^2\) hoặc \(\left(\sqrt{a}\pm\sqrt{b}\right)^2\) rồi phá căn)
a. \(\left(4\sqrt{2}+\sqrt{30}\right).\left(\sqrt{5}-\sqrt{3}\right).\sqrt{4-\sqrt{15}}\)
b. \(\dfrac{\sqrt{3}+1}{2}.\sqrt{8-2\sqrt{3}}\)
So sánh:
a) \(-\dfrac{1}{3}\sqrt{63}và-2\sqrt{2}\)
b) \(-2\sqrt{55}và-\dfrac{3}{5}\sqrt{750}\)
c) \(-3\sqrt{7}và-\dfrac{1}{2}\sqrt{260}\)
Giải 5 câu sau:
1. \(\dfrac{\sqrt{5}+2}{\sqrt{5}-2}\)
2. \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}\)
3. \(\dfrac{\sqrt{20}-3\sqrt{10}}{3-\sqrt{5}}\)
4. \(\dfrac{6-2\sqrt{5}}{3+\sqrt{5}}\)
5. \(\dfrac{9+4\sqrt{5}}{\sqrt{5}+2}\)