làm bài này đâu nhất thiết phải dùng cách nào đâu bạn, vận dụng cách khoa học nhất là đc rồi nhé 

a, bạn tự vẽ 

b, Theo bài ra ta có hệ 

\(\left\{{}\begin{matrix}2x^2+4x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x^2+4x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+1\right)^2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)

Vậy (P) cắt (d) tại A(-1;2) 

8:

a: 

b: PTHĐGĐ là:

2x^2+4x+2=0

=>x=-1

=>y=2

Lời giải:

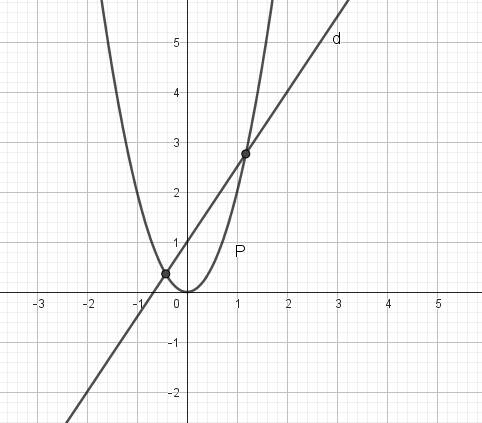
b. PT hoành độ giao điểm:

$2x^2=\frac{3}{2}x+1$

$\Leftrightarrow 4x^2-3x-2=0$

$\Leftrightarrow x=\frac{3\pm \sqrt{41}}{8}$

$x=\frac{3+\sqrt{41}}{8}\Rightarrow y=\frac{3}{2}x+1=\frac{25+3\sqrt{41}}{16}$. Ta có giao điểm $(\frac{3+\sqrt{41}}{8}; \frac{25+3\sqrt{41}}{16})$

$x=\frac{3-\sqrt{41}}{8}\Rightarrow y=\frac{25-3\sqrt{41}}{16}$. Ta có giao điểm $(\frac{3-\sqrt{41}}{8}; \frac{25-3\sqrt{41}}{16})$

a: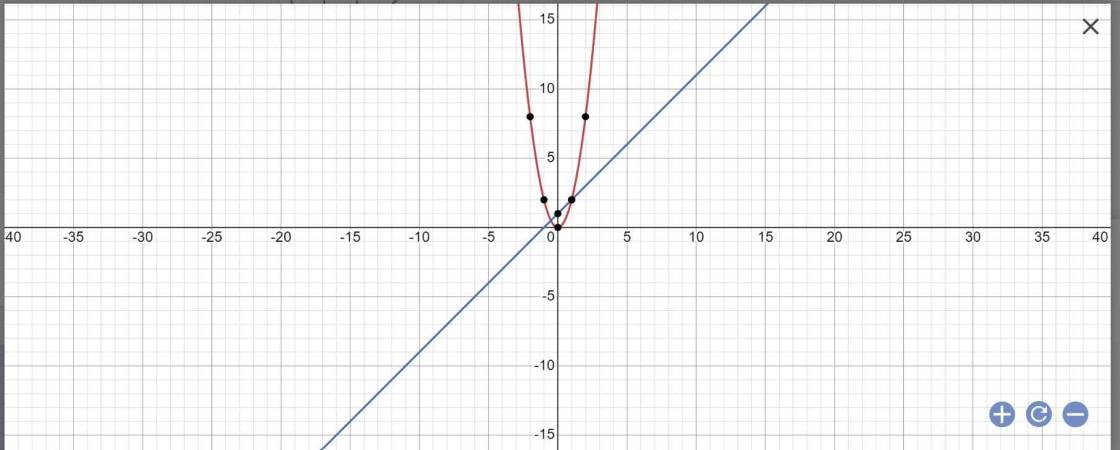 

b: PTHĐGĐ là:

2x^2=x+1

=>2x^2-x-1=0

=>2x^2-2x+x-1=0

=>(X-1)(2x+1)=0

=>x=-1/2 hoặc x=1

=>y=2*1/4=1/2 hoặc y=2

Xét pt hoành độ gđ của (P) và (d):

\(2x^2=mx+1\)

\(\Leftrightarrow2x^2-mx-1=0\)  (1)

Có ac=2.(-1)=-2 => Pt (1) luôn có hai nghiệm pb trái dấu => (d) luôn cắt (P) tại hai điểm nằm khác phía nhau so với trục tung.

Giả sử \(A\left(x_1;2x^2_1\right);B\left(x_2;2x^2_2\right)\) là hai gđ của (d) và (P) với x_1;x₂ là hai nghiệm của pt (1)

Giả sử x₁<0<x₂

Gọi A' ; B' là hình chiếu của A và B lên trục Ox

=>\(AA'=2x^2_1;BB'=2x^2_2\)

\(OA'=\left|x_1\right|=-x_1\) ; \(OB'=\left|x_2\right|=x_2\)

Có \(S_{OAB}=S_{A'ABB'}-S_{OAA'}-S_{OBB'}\)

\(\Leftrightarrow\dfrac{3m}{2}=\dfrac{1}{2}.A'B'\left(AA'+BB'\right)-\dfrac{1}{2}.OA'.AA'-\dfrac{1}{2}.OB'.BB'\)

\(\Leftrightarrow3m=\left(-x_1+x_2\right)\left(2x^2_1+2x^2_2\right)+x_1.2x^2_1-x_2.2x^2_2\)

\(\Leftrightarrow3m=-2x_1^3-2x_1.x_2^2+2x_1^2.x_2+2x_2^3+2x_1^3-2x_2^3\)

\(\Leftrightarrow3m=2x_1x_2\left(x_1-x_2\right)\)

\(\Leftrightarrow3m=2.\left(-\dfrac{1}{2}\right).-\sqrt{\left(x_1-x_2\right)^2}\) (do x₁<x₂ =>x₁-x₂<0)

\(\Leftrightarrow3m=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)\(=\sqrt{\left(\dfrac{m}{2}\right)^2-4.\left(-\dfrac{1}{2}\right)}\)\(=\sqrt{\dfrac{m^2}{4}+2}\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\9m^2=\dfrac{m^2}{4}+2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m^2=\dfrac{8}{35}\end{matrix}\right.\)\(\Rightarrow m=\dfrac{2\sqrt{70}}{35}\)

Vậy...

(Bạn kiểm tra lại xem, có thể mk sẽ tính nhầm nhưng dạng làm vẫn như thế)

\(\left(P\right):y=-2x^2\)

\(\left(d\right):y=ax+b\)

Xét pt hoành độ gđ của (P) và (d) có:

\(-2x^2=ax+b\)

\(\Leftrightarrow-2x^2-ax-b=0\)

Do (P) và (d) giao với nhau tại hai điểm có hoành độ lần lượt là -1;2

=> \(\left\{{}\begin{matrix}-2\left(-1\right)^2-a\left(-1\right)-b=0\\-2.\left(2\right)^2-2a-b=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-4\end{matrix}\right.\)

Vậy...

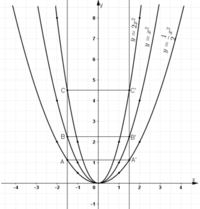
Lấy các điểm A’, B’, C’ lần lượt nằm trên 3 đồ thị và có hoành độ bằng 1,5.

Từ điểm (1,5;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị 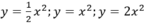lần lượt tại các điểm A,B,C.

Gọi yA,yB,yC lần lượt là tung độ của các điểm A,B,C. Ta có:

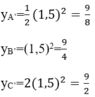
Khi đó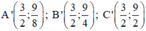 

Nhận xét: A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy.

a: Trục đối xứng là x=-(-1)/4=1/4

Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot2\cdot\left(-2\right)}{4\cdot2}=-\dfrac{17}{8}\end{matrix}\right.\)

Thay y=0 vào (P), ta được:

2x^2-x-2=0

=>\(x=\dfrac{1\pm\sqrt{17}}{4}\)

thay x=0 vào (P), ta được:

y=2*0^2-0-2=-2

b: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{-\left(-6\right)}{2\cdot\left(-3\right)}=\dfrac{6}{-6}=-1\\y=-\dfrac{\left(-6\right)^2-4\cdot\left(-3\right)\cdot4}{4\cdot\left(-3\right)}=7\end{matrix}\right.\)

=>Trục đối xứng là x=-1

Thay y=0 vào (P), ta được:

-3x^2-6x+4=0

=>3x^2+6x-4=0

=>\(x=\dfrac{-3\pm\sqrt{21}}{3}\)

Thay x=0 vào (P), ta được:

y=-3*0^2-6*0+4=4

c: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{-\left(-1\right)}{2\cdot\left(-2\right)}=\dfrac{1}{-4}=\dfrac{-1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot\left(-2\right)\cdot2}{4\cdot\left(-2\right)}=\dfrac{17}{8}\end{matrix}\right.\)

=>Trục đối xứng là x=-1/4

Thay y=0 vào (P), ta được:

-2x^2-x+2=0

=>2x^2+x-2=0

=>\(x=\dfrac{-1\pm\sqrt{17}}{4}\)

Thay x=0 vào (P), ta được:

y=-2*0^2-0+2=2

b. Phương trình hoành độ giao điểm:

\(x^2=4x-m\Leftrightarrow x^2-4x+m=0\) (1)

d cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm pb

\(\Leftrightarrow\Delta'=4-m>0\Rightarrow m< 4\)

Khi đó kết hợp hệ thức Viet và điều kiện đề bài:

\(\left\{{}\begin{matrix}x_1+x_2=4\\2x_1+x_2=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=4\\x_1=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-9\\x_2=13\end{matrix}\right.\)

Mà \(x_1x_2=m\)

\(\Rightarrow m=-9.13=-117\)

a) Thay m=6 vào (d), ta được: y=4x-6

Phương trình hoành độ giao điểm của (P) và (d) là:

\(2x^2=4x-6\)

\(\Leftrightarrow2x^2-4x+6=0\)

\(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot6=16-48=-32\)(loại)

Vì Δ<0 nên phương trình vô nghiệm

Vậy: Khi m=6 thì (P) và (d) không có điểm chung