Cho hình vẽ sau biết \(\widehat{A_1}\)= \(_{_{ }}30^o\); \(\widehat{D_1}\)= \(30^o\)
a) CM a // b
b) Đường thẳng d \(\perp\) b. Tính \(\widehat{ACB}\)?
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
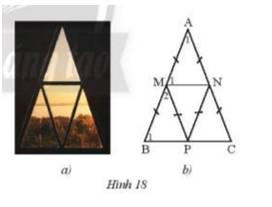
a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau
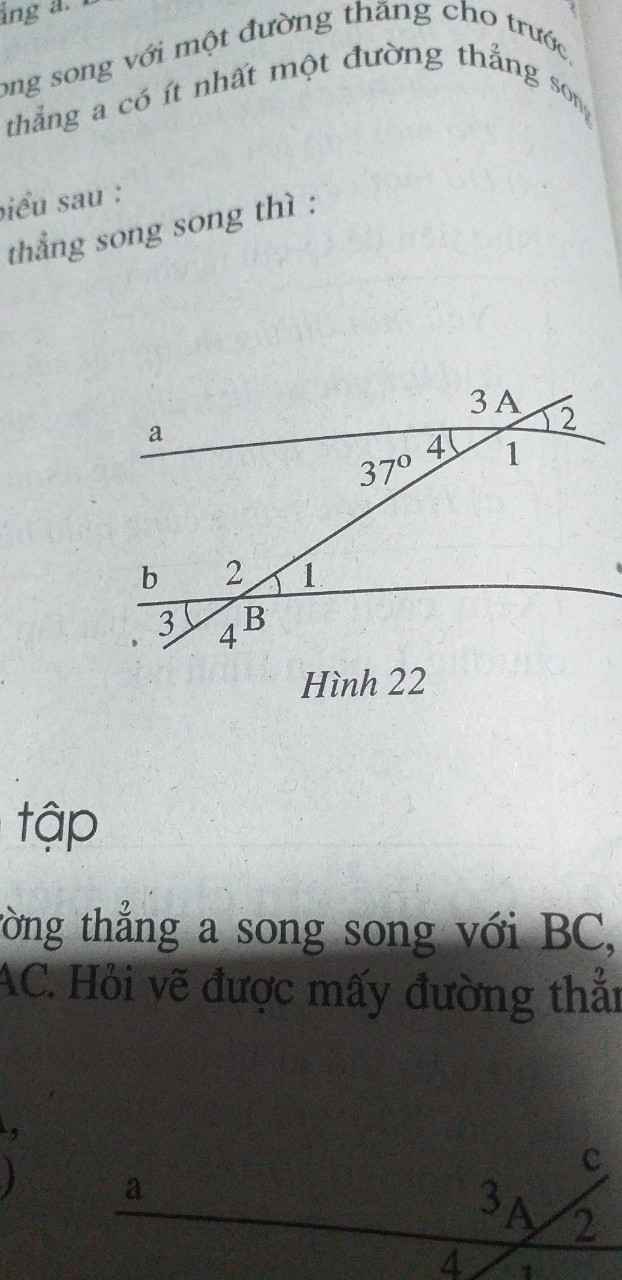
Hình 22 cho biết a // b và \(\widehat{A}_4\) = \(37^o\) .
a) Tính \(\widehat{B_1}\) .
b) So sánh \(\widehat{A_1}\) và \(\widehat{B_4}\) .
c) Tính \(\widehat{B_2}\)
Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) của tứ giác \(ABCD\) (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh \(AB\) và \(CD\); \(AD\) và \(BC\).
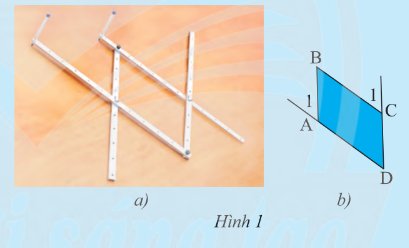
Sau khi đo góc ta thấy cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) bằng nhau
Mà các góc ở vị trí đồng vị
Suy ra: \(AB\) // \(CD\); \(AD\) // \(BC\)
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
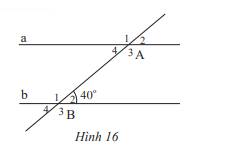
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
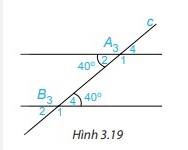
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
Cho hình vẽ
Biết My//Ax,\(\widehat{yMc}\)=30o,\(\widehat{MCA}\)=48O,AZ là tia phân giác của \(\widehat{CAt}\)
tinh số đo góc tAz
Cho hình vẽ sau:

Biết:
- \(\widehat{xOz}\) kề bù \(\widehat{yOz}\)
- Om tia phân giác \(\widehat{xOz}\)
- On \(\perp\) Om tại O
- Au tia phân giác của \(\widehat{yAt}\)
- At song song Oz
a) Chứng minh: On tia phân giác của \(\widehat{yOz}\)
b) Chứng minh: Au \(\perp\) Om
Đề không sai!
a: Ta có: Om là phân giác của góc xOz
=>\(\widehat{xOm}=\widehat{zOm}=\dfrac{1}{2}\cdot\widehat{xOz}\)
Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{zOm}+\widehat{yOz}=2\left(\widehat{zOm}+\widehat{zOn}\right)\)
=>\(\widehat{yOz}=2\cdot\widehat{zOm}+2\cdot\widehat{zOn}-2\cdot\widehat{zOm}=2\cdot\widehat{zOn}\)
=>On là phân giác của góc yOz
b: Ta có: At//Oz
=>\(\widehat{tAy}=\widehat{zOy}\)(hai góc đồng vị)
mà \(\widehat{yAu}=\dfrac{\widehat{yAt}}{2}\)(Au là phân giác của góc yAt)
và \(\widehat{yOn}=\dfrac{\widehat{yOz}}{2}\)(On là phân giác của góc yOz)
nên \(\widehat{yAu}=\widehat{yOn}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Au//On
mà On\(\perp\)Om
nên Au\(\perp\)Om
Trên nửa mặt phẳng bờ tia \(O\)\(x\).Vẽ tia \(Oy\) và \(Oz\) sao cho \(\widehat{xOy}\)\(=30^o\) ,\(\widehat{xOz}\)\(=100^o\).Vẽ tia \(Ot\) trong \(\widehat{yOz}\) sao cho \(\widehat{yOt}\)\(=20^o\).
a)Tính \(\widehat{yOz}\)
b)Tia \(Ot\) có phải là tia phân giác của \(\widehat{yOz}\) không.Vì sao?
c)Giải thích vì sao tia \(Ot\) là tia phân giác của \(\widehat{xOz}\)
Trên nửa mặt phẳng bờ tia chứ tia \(O\)\(x\).Vẽ tia \(Oy\)và \(Oz\)sao cho \(\widehat{xOy}\)\(=30^o\) ,\(\widehat{xOz}\)\(=100^o\).Vẽ tia \(Ot\) trong \(\widehat{yOz}\) sao cho \(\widehat{yOt}\)\(=20^o\).
a)Tính \(\widehat{yOz}\)
b)Tia \(Ot\) có phải là tia phân giác của \(\widehat{yOz}\) không.Vì sao?
c)Giải thích vì sao tia \(Ot\) là tia phân giác của \(\widehat{xOz}\)
a)
vì \(\widehat{xoy}< \widehat{xoz}\left(30^o< 100^o\right)\) nên tia Oy nằm giữ 2 tia Ox và Oz, ta có :
\(\widehat{xoz}=\widehat{xoy}+\widehat{yoz}\)
\(\Rightarrow\widehat{yoz}=\widehat{xoz}-\widehat{xoy}=100^o-30^o=70^o\)
vậy \(\widehat{yoz}=70^o\)
b)
ta có tia ot nằm giữa 2 tia Oy và Oz nên ta có :
\(\widehat{yoz}=\widehat{yot}+\widehat{toz}\)
\(\Rightarrow\widehat{toz}=\widehat{yoz}-\widehat{yot}=70^o-20^o=50^o\)
ta có Ot nằm giữa 2 tia Oy và Oz
vì \(\widehat{toz}=50^o\) nên \(\widehat{toz}\ne\widehat{yot}\left(50^o\ne70^o\right)\) ⇒ tia ot không phải là phân giác của \(\widehat{yoz}\)
c)
ta có tia Ot nằm giữa 2 tia Ox và Oz nên
\(\widehat{xoz}=\widehat{xot}+\widehat{toz}\)
\(\Rightarrow\widehat{xot}=\widehat{xoz}-\widehat{toz}=100^o-50^o=50^o\)
vì tia Ot nằm giữa 2 tia Ox và Oz
và \(\widehat{xot}=\widehat{toz}\left(=50^o\right)\) nên tia Ot là phân giác của \(\widehat{xoz}\)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(30^0< 100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
\(\Leftrightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
\(\Leftrightarrow\widehat{yOz}+30^0=100^0\)
hay \(\widehat{yOz}=70^0\)
Vậy: \(\widehat{yOz}=70^0\)
+)Trên nửa mặt phẳng bờ chứa tia Ox có:∠xOy<∠xOz(30o<100o)
=>Oy là tia phân giác của Ox và Oz
+)Oy là tia phân giác của Ox và Oz
=>∠xOy+∠yOz=∠xOz
=>30o+∠yOz=100o
=>∠yOz=100o-30o=70o
Vậy ∠yOz=70o
b)+)Trên nửa mặt phẳng bờ chứa tia Oy có:∠yOt<∠yOz(20o<70o)
=>Ot nằm giữa 2 tia Oy và Oz
+)Ot nằm giữa 2 tia Oy và Oz
=>∠yOt+∠tOz=∠yOz
=>20o+∠tOz=70o
=>∠tOz=70o-20o=50o
=>∠tOz\(\ne\)∠tOy
=>Ot không phải tia phân giác của ∠yOz
c)+)Oy nằm giữa 2 tia Ox và Oz
Ot nằm giữa 2 tia Oy và Oz
=>Oy nằm giữa 2 tia Ot và Ox
+)Oy nằm giữa 2 tia Ot và Ox
=>∠xOy+∠yOt=∠xOt
=>30o+20o=∠xOt
=>50o=∠xOt
+)Ta có:∠xOt=∠tOz(=50o)(1)
+)Ot nằm giữa 2 tia Oy và Oz
Oy nằm giữa 2 tia Ox và Oz
=>Ot nằm giữa 2 tia Ox và Oz(2)
+)Từ (1) và (2)
=>Ot là tia phân giác của ∠xOz
Chúc bn học tốt