Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng \(\left(a;+\infty\right)\)
Chứng minh rằng nếu \(\lim\limits_{x\rightarrow+\infty}=-\infty\) thì luôn tồn tại ít nhất một số c thuộc \(\left(a;+\infty\right)\) sao cho \(f\left(c\right)< 0\)
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
a) Tìm tập xác định của mỗi hàm số đã cho.
b) Mỗi hàm số trên liên tục trên những khoảng nào? Giải thích.
a) • \(y = f\left( x \right) = \frac{1}{{x - 1}}\)
ĐKXĐ: \(x - 1 \ne 0 \Leftrightarrow x \ne 1\)
Vậy hàm số có tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
• \(y = g\left( x \right) = \sqrt {4 - x} \)
ĐKXĐ: \(4 - x \ge 0 \Leftrightarrow x \le 4\)
Vậy hàm số có tập xác định: \(D = \left( { - \infty ;4} \right]\).
b) • Với mọi \({x_0} \in \left( { - \infty ;1} \right)\), ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{x - 1}} = \frac{{\mathop {\lim }\limits_{x \to {x_0}} 1}}{{\mathop {\lim }\limits_{x \to {x_0}} x - \mathop {\lim }\limits_{x \to {x_0}} 1}} = \frac{1}{{{x_0} - 1}} = f\left( {{x_0}} \right)\)
Vậy hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;1} \right)\).
Tương tự ta có hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( {1; + \infty } \right)\).
Ta có: Hàm số không xác định tại điểm \({x_0} = 1\)
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{x - 1}} = - \infty \)
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
Vậy hàm số \(y = f\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).
• Với mọi \({x_0} \in \left( { - \infty ;4} \right)\), ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {x_0}} 4 - \mathop {\lim }\limits_{x \to {x_0}} x} = \sqrt {4 - {x_0}} = g\left( {{x_0}} \right)\)
Vậy hàm số \(y = g\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;4} \right)\).
Ta có: \(g\left( 4 \right) = \sqrt {4 - 4} = 0\)
\(\mathop {\lim }\limits_{x \to {4^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {4^ - }} 4 - \mathop {\lim }\limits_{x \to {4^ - }} x} = \sqrt {4 - 4} = 0 = g\left( 4 \right)\)
Vậy hàm số \(y = g\left( x \right)\) liên tục tại điểm \({x_0} = 4\).
Hàm số không xác định tại mọi \({x_0} \in \left( {4; + \infty } \right)\) nên hàm số \(y = g\left( x \right)\) không liên tục tại mọi điểm \({x_0} \in \left( {4; + \infty } \right)\).
Vậy hàm số \(y = g\left( x \right)\) liên tục trên nửa khoảng \(\left( { - \infty ;4} \right]\).
Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\) và \({x_0} \in (a;b)\). Điều kiện cần và đủ để hàm số \(y = f(x)\) liên tục tại \({x_0}\) là:
A. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = f\left( {{x_0}} \right)\).
B. \(\mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).
C. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x)\).
D. \(\mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x) = f\left( {{x_0}} \right)\).
Theo lí thuyết ta chọn đáp án D.
Cho hàm số \(y=f\left(x\right)\) xác định và có đạo hàm trên R thỏa mãn: \(\left[f\left(1+2x\right)\right]^3=8x-\left[f\left(1-x\right)\right]^2\), ∀x∈R. viết phương trình tiếp tuyến của đồ thị hàm số \(y=f\left(x\right)\) tại điểm có hoành độ bằng 1.
Câu 48: Cho hàm số y=f(x) có đạo hàm liên tục trên R và \(f'\left(x\right)=x\left(2x-1\right)\left(x^2+3\right)+2\). Hàm số \(y=f\left(3-x\right)+2x+2023\) đồng biến trên khoảng nào trong các khoảng sau?
A: \(\left(-\infty;3\right)\)
B: (3;5)
C: (2;5/2)
D: (5/2;3)
Câu 50: Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=\left(x-1\right)^2\cdot\left(x^2-2x\right)\) với \(\forall x\in R\). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(f\left(x^2-8x+m\right)\) có 5 điểm cực trị?
Cho hàm số \(y=f\left(x\right)\) liên tục trên tập xác định R, và thỏa mãn điều kiện phương trình \(f'\left(x\right)=0\) có 3 nghiệm \(x=-3\) ; \(x=0\) ; \(x=2\). Xét hàm số \(y=g\left(x\right)=f\left(x^2+4x-m\right)\), tính tổng các giá trị nguyên của tham số \(m\in[-10;10]\) để phương trình \(g'\left(x\right)=0\) có đúng 5 nghiệm phân biệt .
A. -6 B. 42 C. 50 D. 6
P/s: Kì thi cuối học kỳ 2 lớp 11 trường THPT Phan Huy Chú , thành phố Hà Nội
Em xin nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán, em cám ơn nhiều ạ!
Cho hàm số \(y=f\left(x\right)=\frac{\sqrt{2-x}-\sqrt{2+x}}{x}\)
a. Tìm điều kiện xác định của hàm số đã cho
b. Tìm trên đồ thị hàm số đã cho các điểm có hoành độ và tung độ là những số nguyên
c. CMR: với mọi giá trị của x thỏa điều kiện xác định trên thì \(f\left(-x\right)=f\left(x\right)\)
a: ĐKXĐ: \(\left\{{}\begin{matrix}-2< =x< =2\\x< >0\end{matrix}\right.\)
c: \(f\left(-x\right)=\dfrac{\sqrt{2-\left(-x\right)}-\sqrt{2+\left(-x\right)}}{-x}=\dfrac{\sqrt{2+x}-\sqrt{2-x}}{-x}=\dfrac{\sqrt{2-x}-\sqrt{2+x}}{x}=f\left(x\right)\)
1. Chứng minh rằng mọi hàm \(f:ℝ\rightarrowℝ\) thỏa mãn \(f\left(xy+x+y\right)=f\left(xy\right)+f\left(x\right)+f\left(y\right),\forall x,y\inℝ\)
2. Xác định tất cả các hàm số \(f\) liên tục trên \(ℝ\) thỏa mãn điều kiện \(f\left(2x-y\right)=2f\left(x\right)-f\left(y\right),\forall x,y\inℝ\)
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
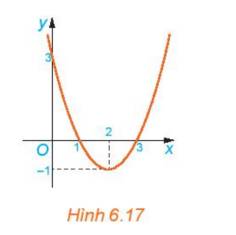
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
Cho hàm số \(f\left(x\right)\) xác định trên \(R\), có đạo hàm \(f'\left(x\right)=\left(x^2-4\right)\left(x-5\right)\forall x\in R\) và \(f\left(1\right)=0\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g\left(x\right)=\left|f\left(x^2+1\right)-m\right|\) có nhiều điểm cực trị nhất?
A.7 B. 8 C. 5 D. 6

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị như Hình 22.
a) Có nhận xét gì về đồ thị hàm số trên mỗi đoạn \(\left[ {a;a + T} \right],\left[ {a + T;a + 2T} \right],\left[ {a - T;a} \right]\)?
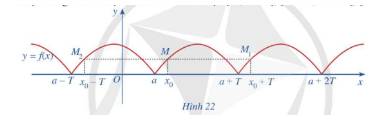
b) Lấy điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) thuộc đồ thị hàm số với \({x_0} \in \left[ {a;a + T} \right]\). So sánh mỗi giá trị \(f\left( {{x_0} + T} \right);f\left( {{x_0} - T} \right)\) với \(f\left( {{x_0}} \right)\)
a) Đồ thị hàm số trên mỗi đoạn là như nhau
b) \(f\left( {{x_0} + T} \right) = f\left( {{x_0} - T} \right) = f\left( {{x_0}} \right)\)