Giúp mình vs toán 1 đh ạ cảm ơn nhiều

Giúp mik giải bài tập toán vs ạ mik cảm ơn rất nhiều ạ 
Bài cuối mình không thấy rõ đề nhưng mình đoán là thế này bạn nhé.
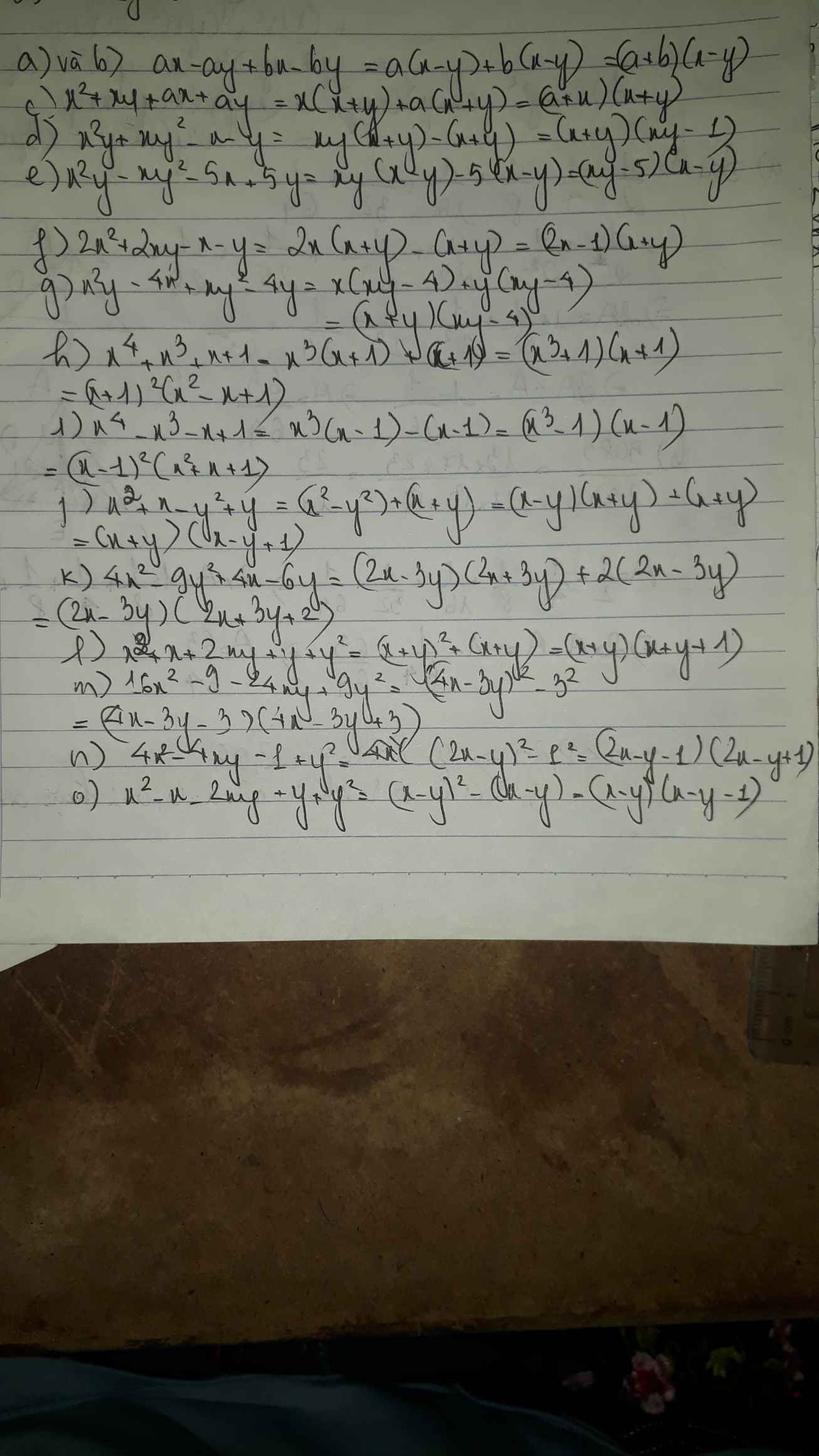
a.
$ax-ay+bx-by=(ax-ay)+(bx-by)=a(x-y)+b(x-y)$
$=(a+b)(x-y)$
b. Trùng phần a
c.
$x^2+xy+ax+ay=(x^2+xy)+(ax+ay)=x(x+y)+a(x+y)$
$=(x+a)(x+y)$
d.
$x^2y+xy^2-x-y=(x^2y+xy^2)-(x+y)$
$=xy(x+y)-(x+y)=(xy-1)(x+y)$
e.
$x^2y-xy^2-5x+5y=(x^2y-xy^2)-(5x-5y)$
$=xy(x-y)-5(x-y)=(x-y)(xy-5)$
f. Biểu thức không phân tích được thành nhân tử
g.
$x^2y-4x+xy^2-4y$
$=(x^2y+xy^2)-(4x+4y)=xy(x+y)-4(x+y)=(x+y)(xy-4)$
h.
$x^4+x^3+x+1=(x^4+x^3)+(x+1)$
$=x^3(x+1)+(x+1)=(x^3+1)(x+1)=(x+1)(x^2-x+1)(x+1)$
$=(x+1)^2(x^2-x+1)$
Mấy bạn giỏi toán gải giúp em vs ạ em cảm ơn rất nhiều mong đc giải nhanh ạ
Mn giải giúp mình vs ạ. Mình cảm ơn nhiều
- Xét : \(x^2+8x-20\le0\)
\(\Rightarrow-10\le x\le2\)
Mà \(x>0\)
\(\Rightarrow0< x\le2\)
- Xét \(x^2-2\left(m+3\right)x+m^2-2m< 0\)
Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)
\(=m^2+6m+9-m^2+2m=8m+9\)
- Để bất phương trình có nghiệm
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow m>-\dfrac{9}{8}\)
=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)
Mà \(0< x\le2\)
\(\Rightarrow0< x_1< x_2\le2\)
\(TH1:x=2\)
\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)
\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)
\(TH2:0< x_1< x_2< 2\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)
Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)
Từ pt đầu \(\Rightarrow-10\le x\le2\) (1)
Để BPT chứa m có nghiệm thì \(\Delta'>0\Rightarrow m...\) (2)
Gọi 2 nghiệm của pt chứa m là \(x_1;x_2\Rightarrow\) miền nghiệm của BPT dưới là \(D=\left(x_1;x_2\right)\)
Do (1) chỉ chứa 2 số nguyên dương là 1 và 2, nên để hệ có nghiệm nguyên dương thì D cần chứa ít nhất 1 trong 2 giá trị 1 hoặc 2
\(\Leftrightarrow\left[{}\begin{matrix}x_1< 1< x_2\\x_1< 2< x_2\end{matrix}\right.\) (các trường hợp trùng lặp 2 điều kiện ví dụ \(x_1< 1< 2< x_2\) không thành vấn đề vì cuối cùng ta cũng hợp nghiệm)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(1\right)< 0\\f\left(2\right)< 0\end{matrix}\right.\) (3) với \(f\left(x\right)=x^2-2\left(m+3\right)x+m^2-2m\)
Lấy giao nghiệm của (2) và (3) sẽ được khoảng m cần tìm
Mn giải giúp mình vs ạ. Mình cảm ơn nhiều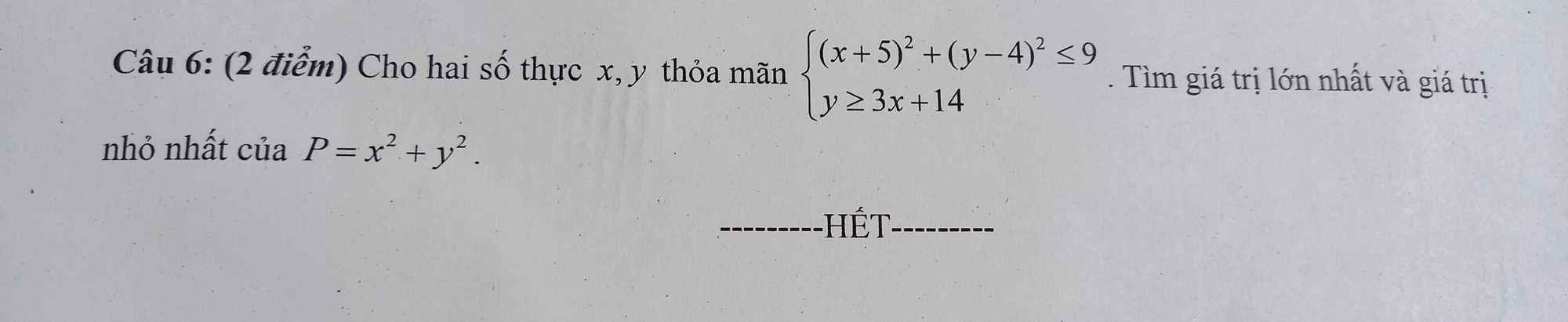
Nếu \(y\le0\Rightarrow\left(y-4\right)^2\ge16>9\left(ktm\right)\Rightarrow y>0\)
Nếu \(x\ge0\Rightarrow\left(x+5\right)^2\ge25>9\left(ktm\right)\Rightarrow x< 0\)
Đặt \(\left\{{}\begin{matrix}-x=a>0\\y=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(a-5\right)^2+\left(b-4\right)^2\le9\\3a+b\ge14\end{matrix}\right.\)
Ta có:
\(14^2\le\left(3a+b\right)^2\le\left(3^2+1\right)\left(a^2+b^2\right)\Rightarrow a^2+b^2\ge\dfrac{196}{10}=\dfrac{98}{5}\)
\(P_{min}=\dfrac{98}{5}\) khi \(\left(a;b\right)=\left(\dfrac{21}{5};\dfrac{7}{5}\right)\) hay \(\left(x;y\right)=\left(-\dfrac{21}{5};\dfrac{7}{3}\right)\)
Lại có:
\(\left(a-5\right)^2+\left(b-4\right)^2\le9\Leftrightarrow a^2+b^2\le10a+8b-32\le\sqrt{\left(10^2+8^2\right)\left(a^2+b^2\right)}-32\)
\(\Rightarrow P\le2\sqrt{41}\sqrt{P}-32\Leftrightarrow P-2\sqrt{41}\sqrt{P}+32\le0\)
\(\Rightarrow\left(\sqrt{P}-3-\sqrt{41}\right)\left(\sqrt{P}-3+\sqrt{41}\right)\le0\) (1)
Do \(P\ge\dfrac{98}{5}\Rightarrow\sqrt{P}-3+\sqrt{41}>0\)
Nên (1) tương đương: \(\sqrt{P}-3-\sqrt{41}\le0\Rightarrow P\le50+6\sqrt{41}\)
\(P_{max}=50+6\sqrt{41}\) khi \(\left(a;b\right)=\left(5+\dfrac{15}{\sqrt{41}};4+\dfrac{12}{\sqrt{41}}\right)\)
Giúp mình bài hình vs ạ mình cảm ơn nhiều
Tìm x biết
\(\dfrac{2x-1}{-12}\)=\(\dfrac{48}{1-2x}\)
Giúp mình vs ạ, mình cảm ơn nhiều
=>(2x-1)^2=24^2
=>2x-1=24 hoặc 2x-1=-24
=>x=-23/2 hoặc x=25/2
\(\dfrac{2x-1}{-12}=\dfrac{48}{1-2x}\) (ĐK: \(x\ne\dfrac{1}{2}\))
\(\Leftrightarrow\dfrac{2x-1}{12}=\dfrac{48}{2x-1}\)
\(\Leftrightarrow-12\cdot48=\left(2x-1\right)\left(2x-1\right)\)
\(\Leftrightarrow567=\left(2x-1\right)^2\)
\(\Leftrightarrow24^2=\left(2x-1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=-24\\2x-1=24\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-23\\2x=25\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{23}{2}\left(tm\right)\\x=\dfrac{25}{2}\left(tm\right)\end{matrix}\right.\)
 mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
Xét pt hoành độ gđ của đường thẳng và parabol có:
\(\left(m-1\right)x^2+3mx+2m=2x-1\)
\(\Leftrightarrow\left(m-1\right)x^2+x\left(3m-2\right)+2m+1=0\) (1)
Để đt và parabol cắt tại hai điểm pb có hoành độ âm
\(\Leftrightarrow\) Pt (1) có hai nghiệm âm phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S< 0\\P>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2-8m+8>0\\\dfrac{2-3m}{m-1}< 0\\\dfrac{2m+1}{m-1}>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;4-2\sqrt{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\\m\in\left(-\infty;\dfrac{2}{3}\right)\cup\left(1;+\infty\right)\\m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(1;+\infty\right)\end{matrix}\right.\)
\(\Rightarrow m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\)
Vậy...
Giúp mình lm bài tập vs ạ mik cảm ơn nhiều ạ 
games: computer games, chess, blind man's buff trò chơi: trò chơi điện tử, cờ vua, bịt mắt bắt dê
sports: football, gymnastics, aerobics thể thao: bóng đá, thể dục dụng cụ, thể dục nhịp điệu
arts and crafts: pottery, painting, making handmade flowers nghệ thuật và thủ công: gốm, vẽ tranh, làm hoa thủ công
other activities: swimming, sleeping, watching TV các hoạt động khác: bơi lội, ngủ, xem TV
Giúp mình vs ạ. Cảm ơn mọi người nhiều
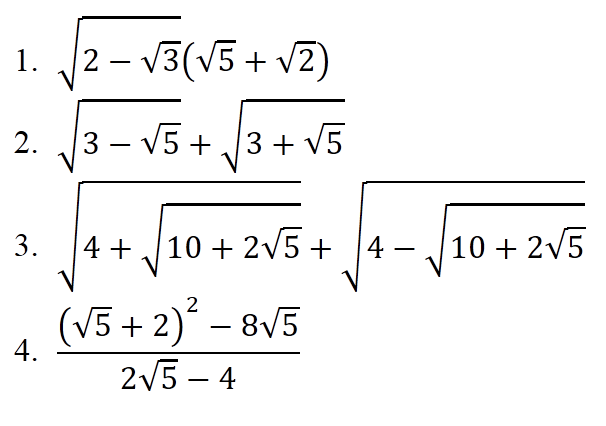
1) \(\sqrt{2-\sqrt{3}}\left(\sqrt{5}+\sqrt{2}\right)=\sqrt{\dfrac{4-2\sqrt{3}}{2}}\left(\sqrt{5}+\sqrt{2}\right)\)
\(=\sqrt{\dfrac{\left(\sqrt{3}-1\right)^2}{2}}\left(\sqrt{5}+\sqrt{2}\right)=\dfrac{\sqrt{3}-1}{\sqrt{2}}\left(\sqrt{5}+\sqrt{2}\right)=\dfrac{\sqrt{15}+\sqrt{6}-\sqrt{5}-\sqrt{2}}{\sqrt{2}}\)
theo mình nghĩ thì đề nên là \(\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\)
như thế thì sẽ \(=\dfrac{\sqrt{3}-1}{\sqrt{2}}.\sqrt{2}\left(\sqrt{3}+1\right)=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)=2\) đẹp hơn,đó là mình nghĩ vậy thôi,còn nếu đề bạn đúng thì mình làm ở trên đó
2) \(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}=\sqrt{\dfrac{6-2\sqrt{5}}{2}}+\sqrt{\dfrac{6+2\sqrt{5}}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{2}}+\sqrt{\dfrac{\left(\sqrt{5}+1\right)^2}{2}}=\dfrac{\sqrt{5}-1}{\sqrt{2}}+\dfrac{\sqrt{5}+1}{\sqrt{2}}=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)
3) Đặt \(A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\)
\(\Rightarrow A^2=8+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\)
\(=8+2\sqrt{16-\left(10+2\sqrt{5}\right)}=8+2\sqrt{6-2\sqrt{5}}\)
\(=8+2\sqrt{\left(\sqrt{5}-1\right)^2}=8+2\sqrt{5}-2=6+2\sqrt{5}=\left(\sqrt{5}+1\right)^2\)
\(\Rightarrow A=\sqrt{5}+1\left(A\ge0\right)\)
4) \(\dfrac{\left(\sqrt{5}+2\right)^2-8\sqrt{5}}{2\sqrt{5}-4}=\dfrac{9+4\sqrt{5}-8\sqrt{5}}{2\left(\sqrt{5}-2\right)}=\dfrac{9-4\sqrt{5}}{2\left(\sqrt{5}-2\right)}\)
\(=\dfrac{\left(\sqrt{5}-2\right)^2}{2\left(\sqrt{5}-2\right)}=\dfrac{1}{2}\)
4) Ta có: \(\dfrac{\left(\sqrt{5}+2\right)^2-8\sqrt{5}}{2\sqrt{5}-4}\)
\(=\dfrac{9-4\sqrt{5}}{2\left(\sqrt{5}-2\right)}\)
\(=\dfrac{\sqrt{5}-2}{2}\)
1) Ta có: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{5}+\sqrt{2}\right)\)
\(=\dfrac{\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{2}}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{2}}\)
\(=\dfrac{\sqrt{15}+\sqrt{6}-\sqrt{5}-\sqrt{2}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{30}+2\sqrt{3}-\sqrt{10}-2}{2}\)
2) Ta có: \(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\)
\(=\dfrac{\sqrt{5}-1+\sqrt{5}+1}{\sqrt{2}}\)
\(=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)
Giúp mình lm bài tập vs ập mình cảm ơn nhiều ạ 