1) \(\sqrt{2-\sqrt{3}}\left(\sqrt{5}+\sqrt{2}\right)=\sqrt{\dfrac{4-2\sqrt{3}}{2}}\left(\sqrt{5}+\sqrt{2}\right)\)
\(=\sqrt{\dfrac{\left(\sqrt{3}-1\right)^2}{2}}\left(\sqrt{5}+\sqrt{2}\right)=\dfrac{\sqrt{3}-1}{\sqrt{2}}\left(\sqrt{5}+\sqrt{2}\right)=\dfrac{\sqrt{15}+\sqrt{6}-\sqrt{5}-\sqrt{2}}{\sqrt{2}}\)
theo mình nghĩ thì đề nên là \(\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\)
như thế thì sẽ \(=\dfrac{\sqrt{3}-1}{\sqrt{2}}.\sqrt{2}\left(\sqrt{3}+1\right)=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)=2\) đẹp hơn,đó là mình nghĩ vậy thôi,còn nếu đề bạn đúng thì mình làm ở trên đó
2) \(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}=\sqrt{\dfrac{6-2\sqrt{5}}{2}}+\sqrt{\dfrac{6+2\sqrt{5}}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{2}}+\sqrt{\dfrac{\left(\sqrt{5}+1\right)^2}{2}}=\dfrac{\sqrt{5}-1}{\sqrt{2}}+\dfrac{\sqrt{5}+1}{\sqrt{2}}=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)
3) Đặt \(A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\)
\(\Rightarrow A^2=8+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\)
\(=8+2\sqrt{16-\left(10+2\sqrt{5}\right)}=8+2\sqrt{6-2\sqrt{5}}\)
\(=8+2\sqrt{\left(\sqrt{5}-1\right)^2}=8+2\sqrt{5}-2=6+2\sqrt{5}=\left(\sqrt{5}+1\right)^2\)
\(\Rightarrow A=\sqrt{5}+1\left(A\ge0\right)\)
4) \(\dfrac{\left(\sqrt{5}+2\right)^2-8\sqrt{5}}{2\sqrt{5}-4}=\dfrac{9+4\sqrt{5}-8\sqrt{5}}{2\left(\sqrt{5}-2\right)}=\dfrac{9-4\sqrt{5}}{2\left(\sqrt{5}-2\right)}\)
\(=\dfrac{\left(\sqrt{5}-2\right)^2}{2\left(\sqrt{5}-2\right)}=\dfrac{1}{2}\)
4) Ta có: \(\dfrac{\left(\sqrt{5}+2\right)^2-8\sqrt{5}}{2\sqrt{5}-4}\)
\(=\dfrac{9-4\sqrt{5}}{2\left(\sqrt{5}-2\right)}\)
\(=\dfrac{\sqrt{5}-2}{2}\)
1) Ta có: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{5}+\sqrt{2}\right)\)
\(=\dfrac{\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{2}}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{2}}\)
\(=\dfrac{\sqrt{15}+\sqrt{6}-\sqrt{5}-\sqrt{2}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{30}+2\sqrt{3}-\sqrt{10}-2}{2}\)
2) Ta có: \(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\)
\(=\dfrac{\sqrt{5}-1+\sqrt{5}+1}{\sqrt{2}}\)
\(=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)

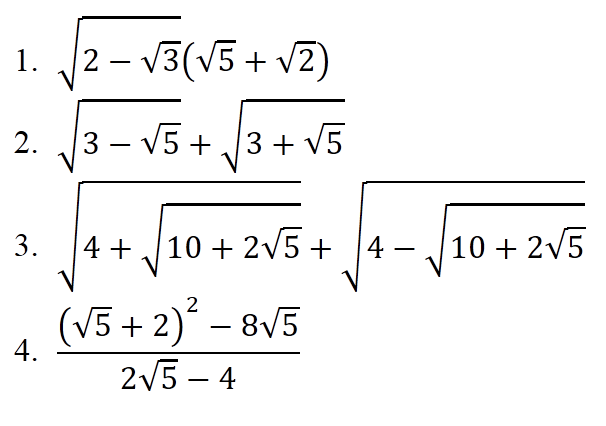






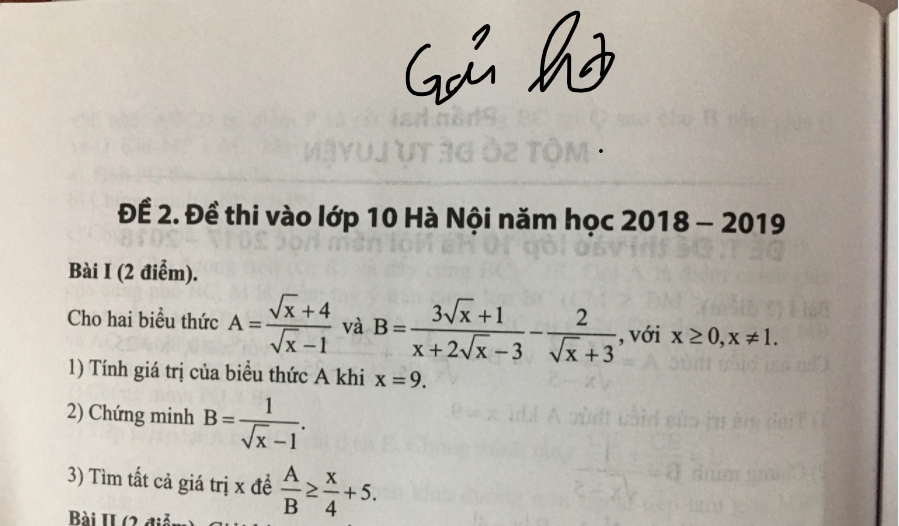







 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !