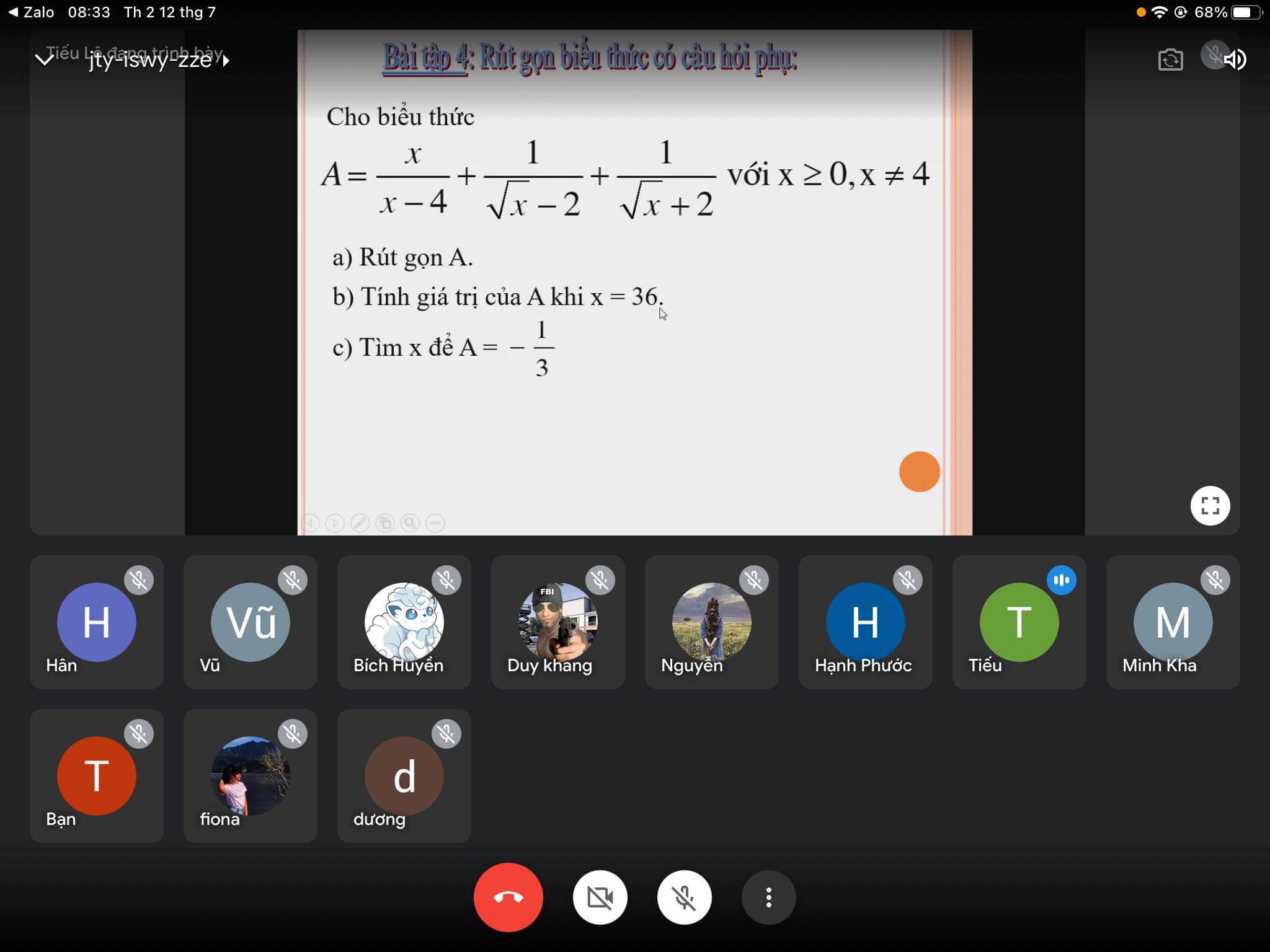
a) Ta có: \(A=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
b) Thay x=36 vào A, ta được:
\(A=\dfrac{6}{6-2}=\dfrac{6}{4}=\dfrac{3}{2}\)
c) Để \(A=\dfrac{-1}{3}\) thì \(\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{-1}{3}\)
\(\Leftrightarrow3\sqrt{x}=-1\left(\sqrt{x}-2\right)\)
\(\Leftrightarrow3\sqrt{x}+\sqrt{x}=2\)
\(\Leftrightarrow\sqrt{x}=\dfrac{1}{2}\)
hay \(x=\dfrac{1}{4}\)













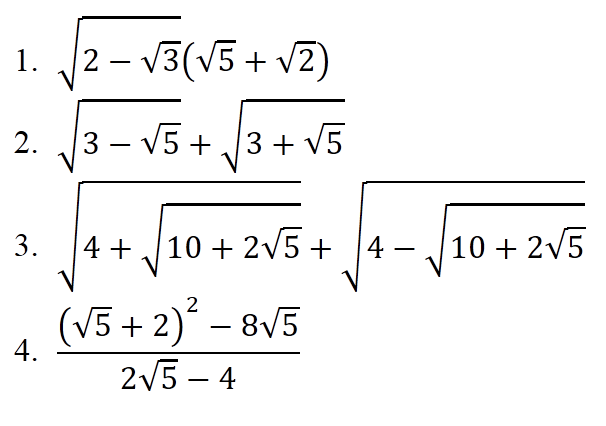



 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !