- Xét : \(x^2+8x-20\le0\)
\(\Rightarrow-10\le x\le2\)
Mà \(x>0\)
\(\Rightarrow0< x\le2\)
- Xét \(x^2-2\left(m+3\right)x+m^2-2m< 0\)
Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)
\(=m^2+6m+9-m^2+2m=8m+9\)
- Để bất phương trình có nghiệm
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow m>-\dfrac{9}{8}\)
=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)
Mà \(0< x\le2\)
\(\Rightarrow0< x_1< x_2\le2\)
\(TH1:x=2\)
\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)
\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)
\(TH2:0< x_1< x_2< 2\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)
Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)
Từ pt đầu \(\Rightarrow-10\le x\le2\) (1)
Để BPT chứa m có nghiệm thì \(\Delta'>0\Rightarrow m...\) (2)
Gọi 2 nghiệm của pt chứa m là \(x_1;x_2\Rightarrow\) miền nghiệm của BPT dưới là \(D=\left(x_1;x_2\right)\)
Do (1) chỉ chứa 2 số nguyên dương là 1 và 2, nên để hệ có nghiệm nguyên dương thì D cần chứa ít nhất 1 trong 2 giá trị 1 hoặc 2
\(\Leftrightarrow\left[{}\begin{matrix}x_1< 1< x_2\\x_1< 2< x_2\end{matrix}\right.\) (các trường hợp trùng lặp 2 điều kiện ví dụ \(x_1< 1< 2< x_2\) không thành vấn đề vì cuối cùng ta cũng hợp nghiệm)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(1\right)< 0\\f\left(2\right)< 0\end{matrix}\right.\) (3) với \(f\left(x\right)=x^2-2\left(m+3\right)x+m^2-2m\)
Lấy giao nghiệm của (2) và (3) sẽ được khoảng m cần tìm







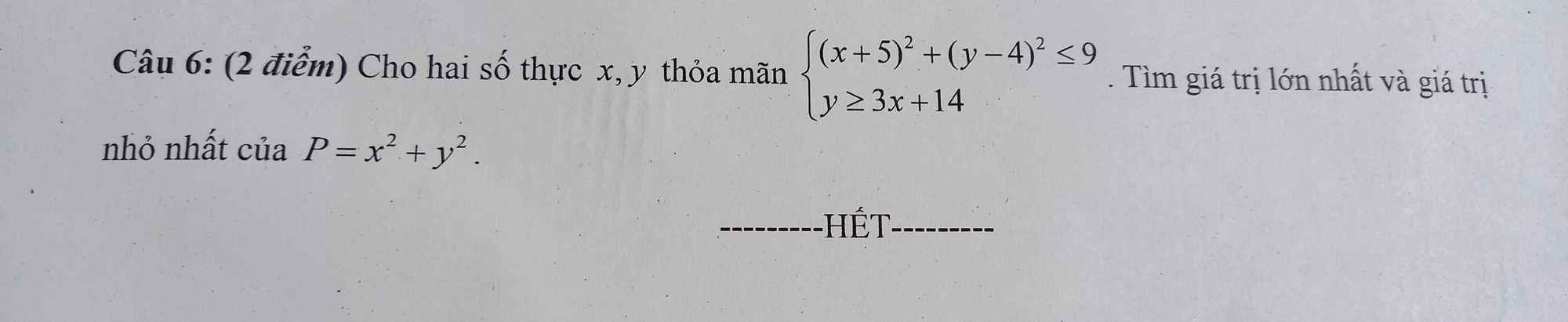


 mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều






