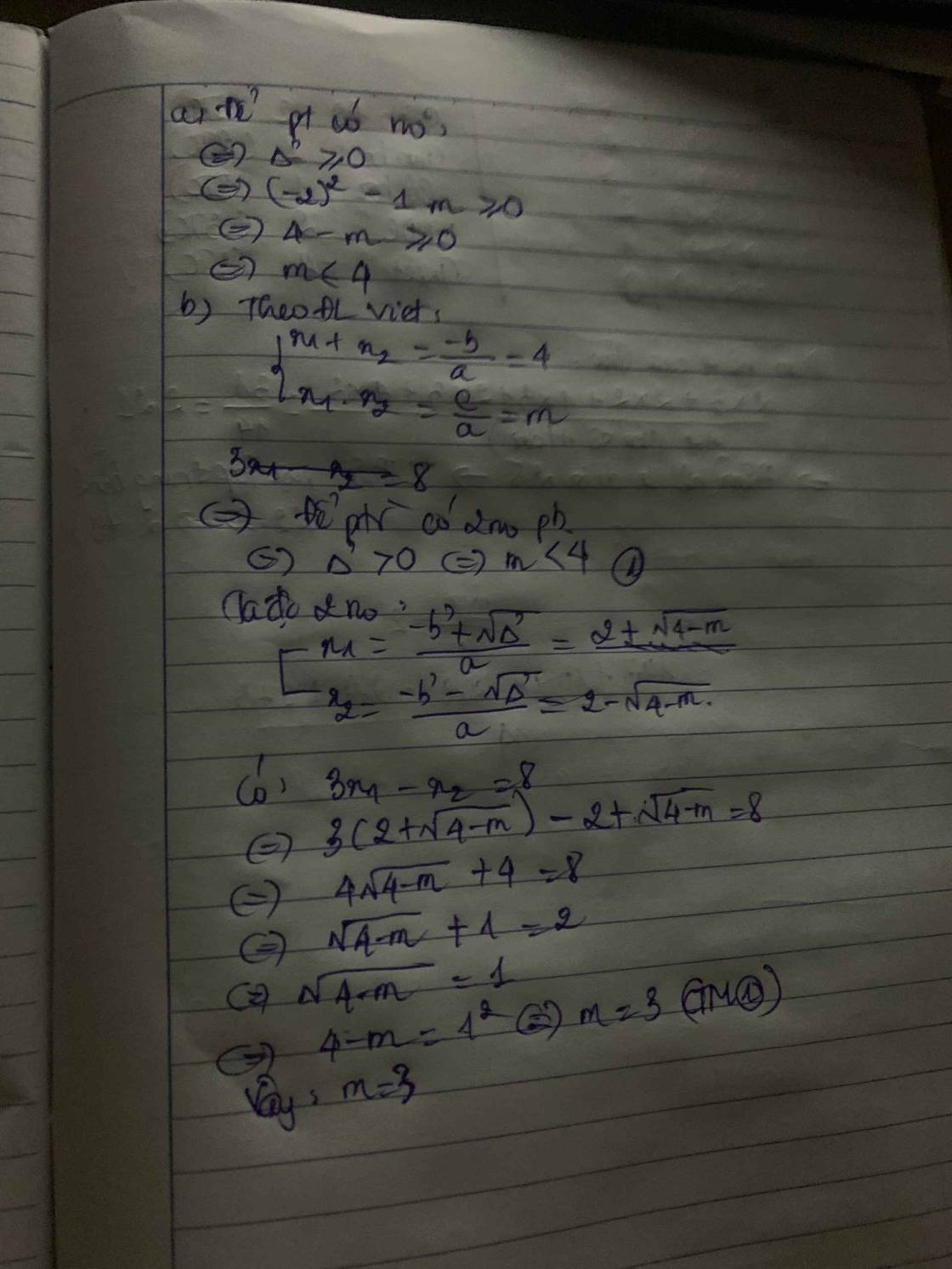Xét m=1 phương trình trở thành \(-4x+1=0\)có nghiệm duy nhất x=-1/4

với m#1 ta có \(\Delta'=\left(m+1\right)^2-m\left(m-1\right)=3m+1\)

với \(\hept{\begin{cases}m\ne1\\m>-\frac{1}{3}\end{cases}}\) pt có hai nghiệm phân biệt

với \(m=-\frac{1}{3}\) pt có nghiệm duy nhất

với \(m< -\frac{1}{3}\)pt vô nghiệm,

theo viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{2\left(m+1\right)}{m-1}=2+\frac{4}{m-1}\\x_1x_2=\frac{m}{m-1}=1+\frac{1}{m-1}\end{cases}}\) lấy phương trình trên trừ đi 4 lần phương trình dưới ta có 

\(x_1+x_2-4x_1x_2=-2\)

ý sau, ta có \(\left|x_1-x_2\right|=\frac{2\sqrt{\Delta'}}{\left|a\right|}=\frac{2\sqrt{3m+1}}{\left|m-1\right|}>2\)

\(\frac{\Leftrightarrow4\left(3m+1\right)}{\left(m-1\right)^2}\ge4\Leftrightarrow m^2-5m\le0\Rightarrow m\in\left[0,5\right]\)

kết hợp với đk có 2 nghiệm phân biệt ở câu a , ta có \(m\in\left[0,5\right]\backslash\left\{1\right\}\)

3.

Phương trình có 2 nghiệm khi:

\(\left\{{}\begin{matrix}m+1\ne0\\\Delta=m^2-12\left(m+1\right)\ge0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}m\ne-1\\\left[{}\begin{matrix}m\ge6+4\sqrt{3}\\m\le6-4\sqrt{3}\end{matrix}\right.\end{matrix}\right.\) (1)

Khi đó theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{m}{m+1}\\x_1x_2=\dfrac{3}{m+1}\end{matrix}\right.\)

Hai nghiệm cùng lớn hơn -1 \(\Rightarrow-1< x_1\le x_2\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1+1\right)\left(x_2+1\right)>0\\\dfrac{x_1+x_2}{2}>-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2+x_1+x_1+1>0\\x_1+x_2>-2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{m+1}-\dfrac{m}{m+1}+1>0\\-\dfrac{m}{m+1}>-2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{m+1}>0\\\dfrac{m+2}{m+1}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-1\\\left[{}\begin{matrix}m>-1\\m< -2\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m>-1\)

Kết hợp (1) \(\Rightarrow\left[{}\begin{matrix}-1< m< 6-4\sqrt{3}\\m\ge6+4\sqrt{3}\end{matrix}\right.\)

Những bài này đều là dạng toán lớp 10, thi lớp 9 chắc chắn sẽ không gặp phải

1. Có 2 cách giải:

C1: đặt \(f\left(x\right)=x^2+2mx-3m^2\)

\(x_1< 1< x_2\Leftrightarrow1.f\left(1\right)< 0\Leftrightarrow1+2m-3m^2< 0\Rightarrow\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\)

C2: \(\Delta'=4m^2\ge0\) nên pt luôn có 2 nghiệm

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-3m^2\end{matrix}\right.\)

\(x_1< 1< x_2\Leftrightarrow\left(x_1-1\right)\left(x_2-1\right)< 0\)

\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1< 0\)

\(\Leftrightarrow-3m^2+2m+1< 0\Rightarrow\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\)

2.

a. Pt có 2 nghiệm cùng dấu khi:

\(\left\{{}\begin{matrix}\Delta'=m^2-5m+4\ge0\\x_1x_2=5m-4>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\ge4\\m\le1\end{matrix}\right.\\m>\dfrac{4}{5}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}m\ge4\\\dfrac{4}{5}< m\le1\end{matrix}\right.\)

Khi đó \(x_1+x_2=2m>2.\dfrac{4}{5}>0\) nên 2 nghiệm cùng dương

b. Pt có 2 nghiệm cùng dấu khi: \(\left\{{}\begin{matrix}m\ne0\\\Delta=m^2-12m\ge0\\x_1x_2=\dfrac{3}{m}>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m\ge12\\m\le0\end{matrix}\right.\\m>0\end{matrix}\right.\) \(\Rightarrow m\ge12\)

Khi đó \(x_1+x_2=-1< 0\) nên 2 nghiệm cùng âm

1.

Yêu cầu bài toán thỏa mãn khi:

\(\left\{{}\begin{matrix}\Delta=25-12m>0\\x_1^2+x_2^2< 17\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(x_1+x_2\right)^2-2x_1x_2< 17\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(2m-3\right)^2-2\left(m^2-4\right)< 17\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\2m^2-12m< 0\end{matrix}\right.\)

\(\Leftrightarrow0< m< \dfrac{25}{12}\)

3.

Yêu cầu bài toán thỏa mãn khi:

\(\left\{{}\begin{matrix}\Delta'=11-m>0\\x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 11\\6>0\\m-2>0\end{matrix}\right.\)

\(\Leftrightarrow2< m< 11\)

Lời giải:

Để pt có 2 nghiệm phân biệt thì:

$\Delta'=4+m^2+5m>0\Leftrightarrow (m+1)(m+4)>0$

$\Leftrightarrow m>-1$ hoặc $m< -4(*)$

Áp dụng định lý Vi-et, với $x_1,x_2$ là nghiệm của pt thì: \(\left\{\begin{matrix} x_1+x_2=-4\\ x_1x_2=-(m^2+5m)\end{matrix}\right.\)

Khi đó:

\(|x_1-x_2|=4\)

\(\Leftrightarrow (x_1-x_2)^2=16\)

\(\Leftrightarrow (x_1+x_2)^2-4x_1x_2=16\)

\(\Leftrightarrow (-4)^2+4(m^2+5m)=16\)

\(\Leftrightarrow m^2+5m+4=4\)

\(\Leftrightarrow m^2+5m=0\Leftrightarrow m(m+5)=0\Rightarrow m=0\) hoặc $m=-5$. Kết hợp với $(*)$ ta thấy 2 giá trị này đều thỏa mãn.

Vậy........

a: Khi x=2 thì pt sẽlà 2^2-4m+3m-4=0

=>-m=0

=>m=0

c: Để PT có hai nghiệm tráo dấu thì 3m-4<0

=>m<4/3

d: Δ=(-2m)^2-4(3m-4)

=4m^2-12m+16

=(2m-3)^2+7>=7

=>Phương trình luôn có hai nghiệm pb

Để PT có 2 nghiệm dương thì 2m>0 và 3m-4>0

=>m>4/3

Giải hộ e bài này vs ạ mọi ng

∆' = (-2)² - [-(m² + 3m)]

= 4 + m² + 3m

= m² + 3m + 9/4 + 7/4

= (m + 3/2)² + 7/4 > 0 với mọi m ∈ R

Vậy phương trình luôn có hai nghiệm phân biệt với mọi m ∈ R

Δ=(-4)^2-4(-m^2-3m)

=16+4m^2+12m

=4m^2+12m+16

Để phương trình có 2 nghiệm phân biệt thì

4m^2+12m+16>0

=>m^2+3m+4>0

=>m^2+3m+9/4+7/4>0

=>(m+3/2)^2+7/4>0(luôn đúng)

???????

ko hiểu

m đâu ra vậy bn