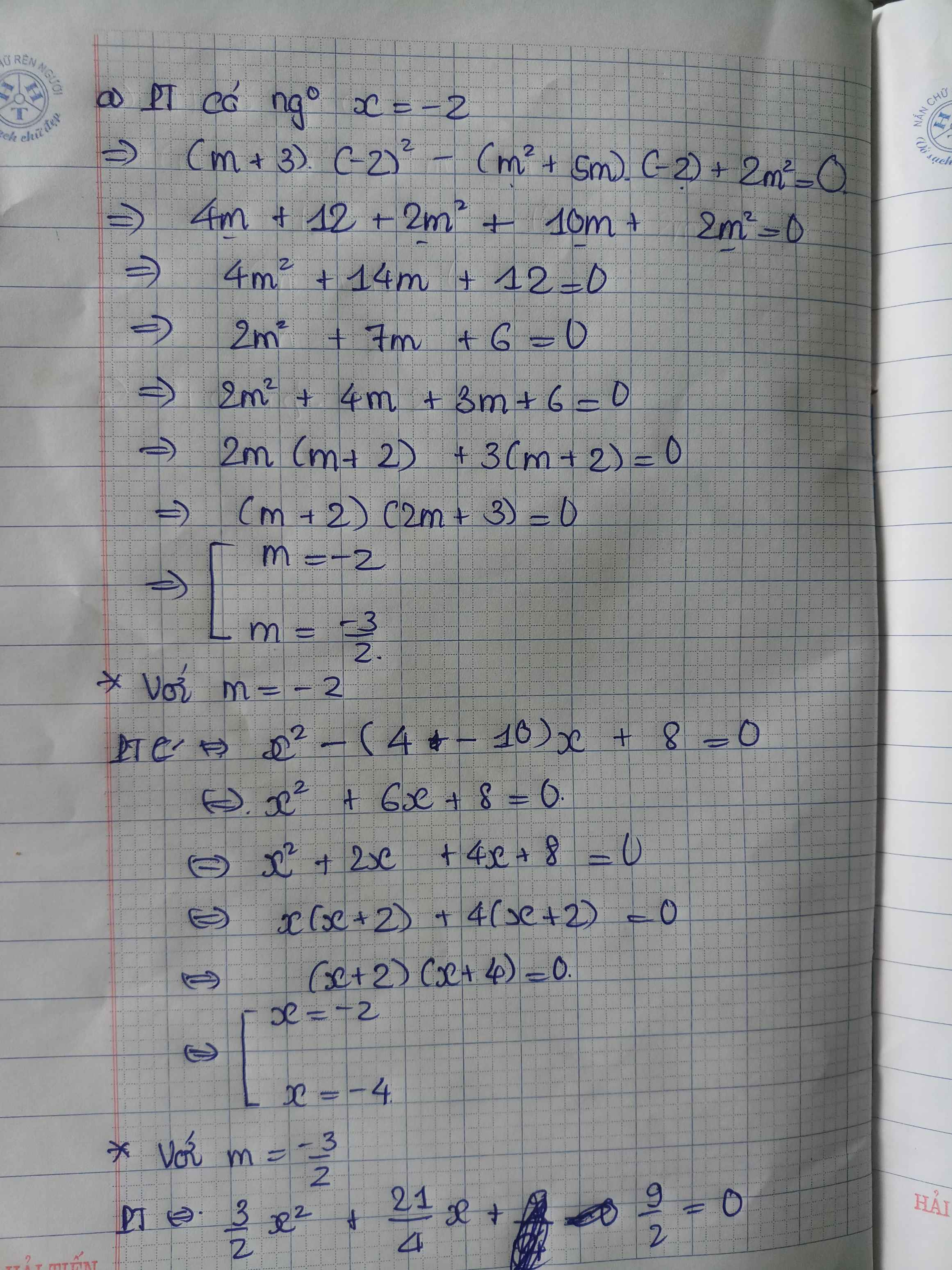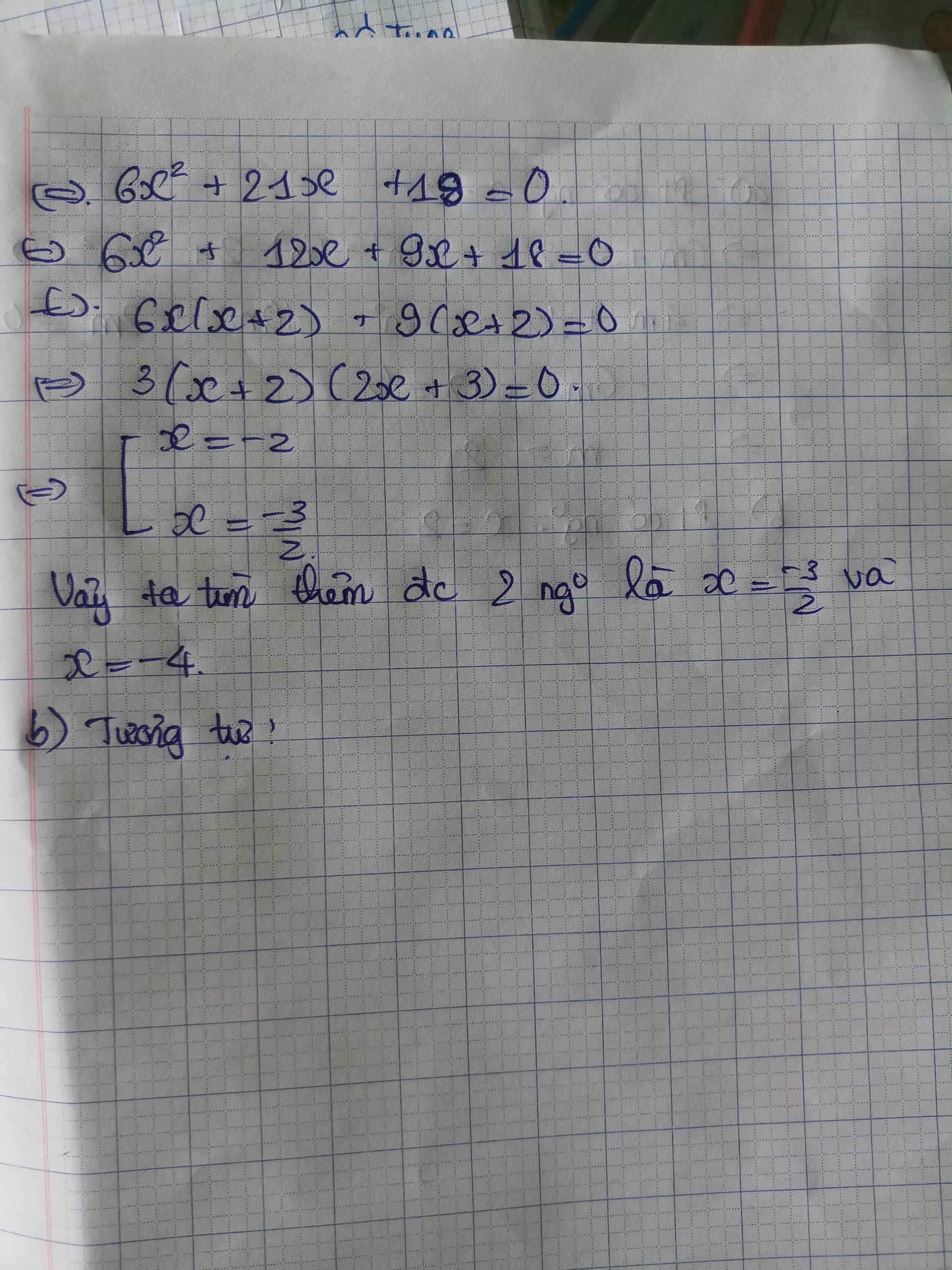PT có nghiệm $x_1=2$

\(\Leftrightarrow4-6\left(m-1\right)+2m-4=0\\ \Leftrightarrow6-4m=0\Leftrightarrow m=\dfrac{3}{2}\)

Theo Vi-ét: \(x_1+x_2=3\left(m-1\right)=\dfrac{3}{2}\)

\(\Leftrightarrow2+x_2=\dfrac{3}{2}\Leftrightarrow x_2=-\dfrac{1}{2}\)

Vậy nghiệm còn lại là $-\frac{1}{2}$

\(x=2\Leftrightarrow4-10+2m+3=0\Leftrightarrow m=\dfrac{3}{2}\\ \Leftrightarrow x^2-5x+6=0\\ \Leftrightarrow\left(x-3\right)\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

Vậy nghiệm còn lại là 3

Để PT có nghiệm bằng \(-1\), thay \(x=-1\) ta có:

\(\left(-1\right)^2-\left(2m-3\right)\left(-1\right)+m^2=0\\ \Leftrightarrow1+2m-3+m^2=0\\ \Leftrightarrow m^2+2m-2=0\Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{3}\\m=-1-\sqrt{3}\end{matrix}\right.\)

Với \(m=-1+\sqrt{3}\Rightarrow x_1x_2=m^2=4-2\sqrt{3}\Rightarrow x_2=-4+2\sqrt{3}\)

Với \(m=-1-\sqrt{3}\Rightarrow x_1x_2=m^2=4+2\sqrt{3}\Rightarrow x_2=-4-2\sqrt{3}\)

Để pt đã cho có nghiệm bằng -1 thì \(1-\left[-\left(2m-3\right)\right]+m^2=0\)\(\Leftrightarrow1+2m-3+m^2=0\)\(\Leftrightarrow m^2+2m-2=0\)\(\Leftrightarrow\left(m+1\right)^2-\left(\sqrt{3}\right)^2=0\)\(\Leftrightarrow\left(m+1+\sqrt{3}\right)\left(m+1-\sqrt{3}\right)=0\)\(\Leftrightarrow m=-1\pm\sqrt{3}\)

Khi đó nghiệm còn lại bằng \(\dfrac{m^2}{1}=\left(-1\pm\sqrt{3}\right)^2=4\mp2\sqrt{3}\)

Khi \(m=-1+\sqrt{3}\) thì nghiệm còn lại bằng \(4-2\sqrt{3}\)

Khi \(m=-1-\sqrt{3}\) thì nghiệm còn lại bằng \(4+2\sqrt{3}\)

phương trình này ạ (2m-1)x^2+(m-3)x-6m-2=0 , phương trình trên mình sửa nó lỗi nên viết xuống đây ạ

\(\left(2m-1\right)x^2+\left(m-3\right)x-6m-2=0\)

\(\Leftrightarrow2mx^2-x^2+mx-3x-6m-2=0\)

\(\Leftrightarrow m\left(2x^2+x-6\right)-\left(x^2+3x+2\right)=0\)

\(\Leftrightarrow m\left(2x-3\right)\left(x+2\right)-\left(x+1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left[m\left(2x-3\right)-\left(x+1\right)\right]=0\)

\(\Leftrightarrow\left(x+2\right)\left(\left(2m-1\right)x-3m-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x+2=0\\\left(2m-1\right)x-3m-1=0\end{matrix}\right.\)

\(\Rightarrow\) Pt luôn có nghiệm \(x=-2\) với mọi m

- Nếu \(2m-1=0\Leftrightarrow m=\dfrac{1}{2}\) pt chỉ có nghiệm duy nhất \(x=-2\)

- Nếu \(m\ne\dfrac{1}{2}\) thì nghiệm còn lại thỏa mãn:

\(\left(2m-1\right)x=3m+1\)

\(\Rightarrow x=\dfrac{3m+1}{2m-1}\)

a: Thay x=-1 vào (6), ta được:

1+2m+m+6=0

=>3m+7=0

=>m=-7/3

x1+x2=-2m/1=-2*7/3=-14/3

=>x2=-14/3-x1=-14/3+1=-11/3

b: \(\text{Δ}=0^2-2\left(2m+m+6\right)=-2\left(3m+6\right)\)

Để phương trình có nghiệm kép thì 3m+6=0

=>m=-2

Khi m=-2 thì (6) sẽ là x^2+2*(-2)-2+6=0

=>x^2-4x+4=0

=>x=2

b) Thay x=2 vào pt, ta được:

\(4\left(m^2-1\right)-4m+m^2+m+4=0\)

\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)

\(\Leftrightarrow5m^2-3m=0\)

\(\Leftrightarrow m\left(5m-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)

Áp dụng hệ thức Vi-et, ta được:

\(x_1+x_2=\dfrac{2m}{m^2-1}\)

\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)

Thay x=1 vào pt, ta được;

\(1-2\left(m-1\right)+2m-5=0\)

=>2m-4-2m+2=0

=>-2=0(vô lý)