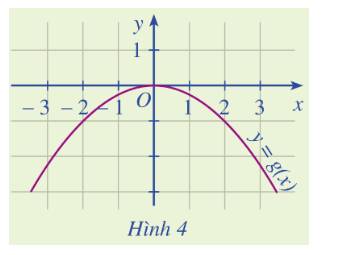
Dựa vào Hình 4, xác định \(g\left( { - 2} \right),g\left( 0 \right),g\left( 2 \right)\).
Cho hàm số \(f\left(x\right)\) xác định trên \(R\), có đạo hàm \(f'\left(x\right)=\left(x^2-4\right)\left(x-5\right)\forall x\in R\) và \(f\left(1\right)=0\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g\left(x\right)=\left|f\left(x^2+1\right)-m\right|\) có nhiều điểm cực trị nhất?
A.7 B. 8 C. 5 D. 6

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m
Cho \(f\left(x\right)=ax^3+4x\left(x^2-1\right)+8\) và \(g\left(x\right)=x^3+4x\left(bx+1\right)+c-3\) xác định a, b, c để \(f\left(x\right)=g\left(x\right)\)
xét đa thức :
a, \(f\left(x\right)=x^2+\left(a+b\right)x+ab\)và \(g\left(x\right)=x^2+5x+6\). xác định a ,b để f(x) = g(x)
b, \(f\left(x\right)=ãx^2+bx+c\)và \(g\left(x\right)=x\left(x+2\right)-\left(x+2\right)\). Xác định a , b để f(x)=g(x)
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
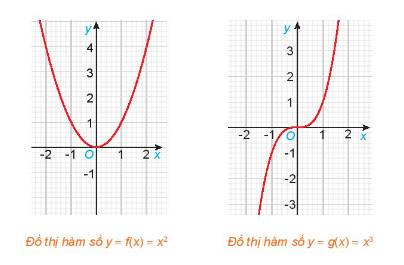
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?
a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)
b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)
Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung
c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} = - {x^3} = - g\left( x \right)\)
Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ
Xác định các hệ số a,b để \(f\left(x\right)=x^4+3x^3-x^2+\left(2a-b\right)x+3b+a\) chia hết cho \(g\left(x\right)=x^2+3x-1\)
f(x) chia hết cho x^2+3x-1
=>(2a-b)=0 và 3b+a=0
=>a=b=0
giải pt sau bằng các định lý : \(f\left(x\right)=g\left(x\right)\Leftrightarrow\left[f\left(x\right)\right]^{2k+1}=\left[g\left(x\right)\right]^{2k+1}\)
\(\sqrt[2k+1]{f\left(x\right)}=g\left(x\right)\Leftrightarrow f\left(x\right)=\left[g\left(x\right)\right]^{2k+1}\)
\(\sqrt[2k+1]{f\left(x\right)}=\sqrt[2k+1]{g\left(x\right)}\Leftrightarrow f\left(x\right)=g\left(x\right)\)
\(\sqrt[2k]{f\left(x\right)}=g\left(x\right)\Leftrightarrow\orbr{\begin{cases}g\left(x\right)>0\\f\left(x\right)=\left[g\left(x\right)\right]^{2k}\end{cases}}\)
\(\sqrt[2k]{f\left(x\right)}=\sqrt[2k]{g\left(x\right)}\Leftrightarrow\hept{\begin{cases}f\left(x\right)\ge0\\g\left(x\right)\ge0\\f\left(x\right)=g\left(x\right)\end{cases}}\)hoặc
a) \(\sqrt{x+1}+\sqrt{4x+13}=\sqrt{3x+12}\)
b)\(\left(x+3\right)\cdot\sqrt{10-x^2}=x^2-x-12\)
c) \(\sqrt{x+4}-\sqrt{1-x}=\sqrt{1-2x}\)
bổ xung định lý thứ 5
f(x)>=0 hoặc g(x)>=0 và f(x)=g(x)
Cho hàm số \(y=f\left(x\right)\) liên tục trên tập xác định R, và thỏa mãn điều kiện phương trình \(f'\left(x\right)=0\) có 3 nghiệm \(x=-3\) ; \(x=0\) ; \(x=2\). Xét hàm số \(y=g\left(x\right)=f\left(x^2+4x-m\right)\), tính tổng các giá trị nguyên của tham số \(m\in[-10;10]\) để phương trình \(g'\left(x\right)=0\) có đúng 5 nghiệm phân biệt .
A. -6 B. 42 C. 50 D. 6
P/s: Kì thi cuối học kỳ 2 lớp 11 trường THPT Phan Huy Chú , thành phố Hà Nội
Em xin nhờ sự giúp đỡ của quý thầy cô giáo và các bạn yêu toán, em cám ơn nhiều ạ!
Cho các dữ kiện sau:
(1) \(H_2O\left(l\right)\rightarrow H_2O\left(g\right)\) \(\Delta_rH_{298}^0=44,01kJ\)
(2) \(H_2\left(g\right)\rightarrow2H\left(g\right)\) \(E_b=435kJ.mol^{-1}\)
(3) \(O_2\left(g\right)\rightarrow2O\left(g\right)\) \(E_b=497kJ.mol^{-1}\)
\(\Delta_fH_{298}^0\) của \(H_2O\left(l\right)\) là -285,83\(kJ.mol^{-1}\)
Tính giá trị năng lượng liên kết O-H trong phân tử nước
Trong phản ứng chuyển hơi của nước, nhiệt động học của phản ứng được thể hiện bởi ΔrH°298 = 44,01 kJ.
Trong phân tử nước, mỗi nguyên tử oxy tích điện âm tạo liên kết cộng hóa trị với hai nguyên tử hydro tích điện dương. Vì vậy, năng lượng liên kết O-H trong phân tử nước bằng nửa năng lượng dissocation của nước, do ΔrH°298 = -ΔfH°298 của nước. Do đó, giá trị năng lượng liên kết O-H trong phân tử nước là:
E(O-H) = 0,5 * (-285,83 kJ/mol) = -142,92 kJ/mol
Vì giá trị này là âm, cho thấy rằng sự tương tác giữa oxy và hydro trong phân tử nước là liên kết hút điện mạnh.
Cho hai hàm số : \(f\left(x\right)=x^2\) và \(g\left(x\right)=3-x\)
a) Tính \(f\left(-3\right)\), \(f\left(-\dfrac{1}{2}\right)\), \(f\left(0\right)\), \(g\left(1\right)\), \(g\left(2\right)\), \(g\left(3\right)\)
b) xác định a để \(2f\left(a\right)=g\left(a\right)\)
Lời giải:
a)
\(f(-3)=(-3)^2=9; f(-\frac{1}{2})=(\frac{-1}{2})^2=\frac{1}{4}\)
\(f(0)=0^2=0\)
\(g(1)=3-1=2; g(2)=3-2=1; g(3)=3-3=0\)
b)
\(2f(a)=g(a)\)
\(\Leftrightarrow 2a^2=3-a\)
\(\Leftrightarrow 2a^2+a-3=0\Leftrightarrow (2a+3)(a-1)=0\)
\(\Rightarrow \left[\begin{matrix} a=\frac{-3}{2}\\ a=1\end{matrix}\right.\)