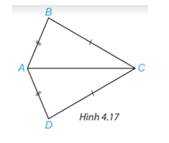
Cho hình 4.17, biết AB=AD, BC=DC. Chứng minh rằng \(\Delta ABC = \Delta ADC\)
Cho ΔABC có AB = BC. Gọi D là trung điểm của BC. Chứng minh rằng.
a) ΔADB = ΔADC
b) AD ⊥ BC
a, Xét \(\Delta ADB;\Delta ADC\) có :
\(\left\{{}\begin{matrix}AB=AC\\DB=DC\\ADchung\end{matrix}\right.\)
\(\Leftrightarrow\Delta ADB=\Delta ADC\left(c-c-c\right)\)
b, \(\Delta ADB=\Delta ADC\left(cmt\right)\)
\(\Leftrightarrow\widehat{BDA}=\widehat{ADC}\)
Lại có :
\(\widehat{BDA}+\widehat{ADC}=180^0\left(kềbuf\right)\)
\(\Leftrightarrow\widehat{BDA}+\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
\(\Leftrightarrow AD\perp BC\)
Cho ΔABC vuông tại A , có AB=12cm; AC=16cm. Kẻ đường cao AH (H∈ BC).
a) Chứng minh : ΔHBA đồng dạng ΔABC
b) Tính độ dài các đoạn thẳng BC, AH
c) Kẻ AD , DE , DF lần lượt là phân giác trong của ΔABC (D∈BC), ΔADB (E∈AB), ΔADC (F∈AC). Chứng minh rằng:\(\dfrac{EA}{EB}.\dfrac{DB}{DC}.\dfrac{FC}{FA}=1\)
Tự kẽ hình nha :
a) Xét tam giác AHB và tam giác ABC có :
\(\widehat{A}\) = \(\widehat{H}\) = 900
\(\widehat{B}\) = góc chung
=.tam giác AHB ~ tam giác CAB ( g.g)
b) ADĐL pitago và tam giác vuông ABC , có :
AB2 + AC2 = BC2
122 + 162 = BC2
BC2 = 400
=> BC = 20 cm
Vì tam giác AHB ~ tam giác CAB ( câu a) , ta có :
\(\dfrac{AH}{AC}\)= \(\dfrac{AB}{BC}\)
=.> \(\dfrac{AH}{16}\)= \(\dfrac{12}{20}\)
=> AH = 9,6 cm
c)
Thay : \(\dfrac{EA}{EB}\)= \(\dfrac{DB}{DC}\)=\(\dfrac{FC}{FA}\)
Thành : \(\dfrac{AD}{DB}\)=\(\dfrac{DB}{BC}\)= \(\dfrac{BC}{AD}\)
Mà : \(\dfrac{AD}{DB}\)=\(\dfrac{DB}{BC}\)=\(\dfrac{BC}{AD}\)= 1
=> \(\dfrac{EA}{EB}\)=\(\dfrac{DB}{DC}\)=\(\dfrac{FC}{FA}\)= 1
Cho \(\Delta ABC\) có AB = AC. D là trung điểm của BC.
a) Chứng minh: \(\Delta ADB\) = \(\Delta ADC\) và AD là tia phân giác của \(\widehat{BAC}\).
b) Vẽ \(DC\perp AD\) tại M. Trên cạnh Ac lấy điểm N sao cho AN = AM. Chứng minh: \(\Delta AMD\) = \(\Delta AND\) và \(DC\perp AN\).
c) Gọi K là trung điểm của NC. Trên tia DK lấy điểm E sao cho K là trung điểm của DE. Chứng minh: \(\Delta KCD\) = \(\Delta KNE\).
d) Chứng minh: MN // BC và 3 điểm M, N, E thẳng hàng.
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
b: Sửa đề: DM\(\perp\)AB tại M. Chứng minh AC\(\perp\)DN
Xét ΔAMD và ΔAND có
AM=AN
\(\widehat{MAD}=\widehat{NAD}\)
AD chung
Do đó: ΔAMD=ΔAND
=>\(\widehat{AMD}=\widehat{AND}\)
mà \(\widehat{AMD}=90^0\)
nên \(\widehat{AND}=90^0\)
=>DN\(\perp\)AC
c: Xét ΔKCD và ΔKNE có
KC=KN
\(\widehat{CKD}=\widehat{NKE}\)(hai góc đối đỉnh)
KD=KE
Do đó: ΔKCD=ΔKNE
d: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
Ta có: ΔKCD=ΔKNE
=>\(\widehat{KCD}=\widehat{KNE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NE//DC
=>NE//BC
ta có: NE//BC
MN//BC
NE,MN có điểm chung là N
Do đó: M,N,E thẳng hàng
Cho \(\Delta\)ABC vuông tại A; AB= 12cm; AC= 16cm. Đương cao AH
a, Chứng minh \(\Delta\)HBA đồng dạng với\(\Delta\)ABC
b, Tính BC, AH
c, trong \(\Delta\)ABC, kẻ phân giác AD. Trong \(\Delta\)ADB kẻ phân giác DE. Trong \(\Delta\)ADC kẻ phân giác DF. Chứng minh \(\dfrac{EA}{EB}\times\dfrac{DB}{DC}\times\dfrac{FC}{FE}=1\)
a) Biết AF = 3,6; FC = 6,4. Tính DF và \(S_{ADC}\)
b) Chứng minh: \(\Delta AEF \backsim \Delta ACB\)
b
Δ ABD ⊥ tại D có DE là đường cao.
=> \(AD^2=AE.AB\) (hệ thức lượng) (1)
Δ ADC ⊥ tại C có DC là đường cao.
=> \(AD^2=AF.AC\) (hệ thức lượng) (2)
Từ (1), (2) suy ra: \(AE.AB=AF.AC\left(=AD^2\right)\)
Xét Δ AEF và Δ ACB có:
\(\widehat{EAF}=\widehat{CAB}\) (góc chung)
\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\left(cmt\right)\)
=> Δ AEF đồng dạng Δ ACB (c.g.c)
a
Theo hệ thức lượng có: \(DF^2=AF.FC=3,6.6,4=23,04\Rightarrow DF=\sqrt{23,04}=4,8\)
\(AC=AF+FC=3,6+6,4=10\)
\(S_{ADC}=\dfrac{1}{2}AC.DF=\dfrac{1}{2}.10.4,8=24\)
Cho ΔABC biết AB = 4,8cm; AC = 6,4cm; BC = 3,6cm. Trên AB lấy D sao cho AD = 3,2cm; trên AC lấy E sao cho AE = 2,4cm. Kéo dài ED cắt CB tại F. a) Chứng minh rằng : ΔABC ∽ ΔAED. b) Chứng minh rằng : ΔFBD ∽ ΔFEC. c) Tính ED, FB.
a: Xét ΔABC và ΔAED có
AB/AE=AC/AD
góc BAE chung
Do đó: ΔABC\(\sim\)ΔAED
b: Xét ΔFBD và ΔFEC có
\(\widehat{FDB}=\widehat{FCE}\left(=\widehat{ADE}\right)\)
góc BFD chung
Do đó: ΔFBD\(\sim\)ΔFEC
c: BD=AB-AD=4,8-3,2=1,6(cm)
EC=AC-AE=6,4-2,4=4(cm)
Ta có: ΔADE\(\sim\)ΔACB
nên DE/CB=AD/AC=3,2/6,4=1/2
=>DE=1,8(cm)
Cho \(\Delta\) ABC, Trên nửa mặt phẳng bờ BC không chứa A, lấy điểm D sao cho DB = AB và DC = AC. Chứng minh rằng BC là trung trực của AD
Cho ΔABC biết AB = 4,8cm; AC = 6,4cm; BC = 3,6cm. Trên AB lấy D sao cho AD = 3,2cm; trên AC lấy E sao cho AE = 2,4cm. Kéo dài ED cắt CB tại F.
a) Chứng minh rằng : ΔABC ∽ ΔAED.
b) Chứng minh rằng : ΔFBD ∽ ΔFEC.
c) Tính ED, FB.
a: Xét ΔABC và ΔAED có
AB/AE=AC/AD
góc BAE chung
Do đó: ΔABC\(\sim\)ΔAED
b: Xét ΔFBD và ΔFEC có
\(\widehat{FDB}=\widehat{FCE}\left(=\widehat{ADE}\right)\)
góc BFD chung
Do đó: ΔFBD\(\sim\)ΔFEC
c: BD=AB-AD=4,8-3,2=1,6(cm)
EC=AC-AE=6,4-2,4=4(cm)
Ta có: ΔADE\(\sim\)ΔACB
nên DE/CB=AD/AC=3,2/6,4=1/2
=>DE=1,8(cm)
Cho \(\Delta\)ABC có AB= AC, E là trung điểm của BC. Trên tia đối của tia EA lấy điểm D sao cho AE= DE.
a) Chứng minh \(\Delta\)ABE= \(\Delta\)DCE
b) Chứng minh AB//DC
c) Chứng minh AE\(\perp\)BC
d) Tìm điều kiện \(\Delta\)ABC để ADC= 45 độ
a) Xét \(\Delta ABE\) và \(\Delta DCE\) có :
BE = EC (E là trung điểm của BC -gt)
\(\widehat{AEB}=\widehat{DEC}\) (đối đỉnh)
AE = ED (gt)
=> \(\Delta ABE\) = \(\Delta DCE\) (c.g.c)
b) Ta có : \(\widehat{CDE}=\widehat{BAE}\) (2 góc tương ứng - \(\Delta ABE\) = \(\Delta DCE\) )
Mà 2 góc này ở vị trí so le trong
=> AB //DC (đpcm)
c) Theo giả thuyết thì ta có :
Trong tam giác ABC có : \(AB=AC\)
=> \(\Delta ABC\) cân tại A
Mà AE là đường trung tuyến trong tam giác
=> AE đồng thời là đường trung trưc trong tam giác
=> \(AE\perp BC\) (đpcm)
d) Để \(\widehat{ADC}=45^o\)
<=> \(\Delta ABC\) vuông cân tại A
a) Xét ΔABE và ΔDCE có :
BE = EC (E là trung điểm của BC -gt)
góc AEB=góc DEC (đối đỉnh)
AE = ED (gt)
=> ΔABE = ΔDCE (c.g.c)
b) Ta có : góc CDE=góc BAE (2 góc tương ứng - tam giác ABE = tam giác DCE )
Mà 2 góc này ở vị trí so le trong
=> AB //DC (đpcm)
c) Theo giả thuyết thì ta có :
Trong tam giác ABC có : AB=AC
=> ΔABC cân tại A
Mà AE là đường trung tuyến trong tam giác
=> AE đồng thời là đường trung trưc trong tam giác
=> AE⊥BC (đpcm)
d) Để góc ADC = 45 độ <=> tam giác ABC vuông cân tại A