Điều kiện xác định của phương trình\(\dfrac{x+2}{x-3}=\dfrac{3x-1}{x\left(x-3\right)}+1\)
A.\(x\ne0;x\ne3\)
B.\(x\ne0;x\ne-3\)
C.\(x\ne0\)
D.\(x\ne\pm3\)
Tìm ĐIỀU KIỆN XÁC ĐỊNH của phương trình \(\dfrac{x}{2\left(x-3\right)}\)+\(\dfrac{x}{2\left(x+1\right)}\)=\(\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)và phương trình \(\dfrac{6}{x-2}\)=\(\dfrac{7}{-x-3}\)
+ Pt thứ nhất :
Ta có mẫu thức chung là : \(2\left(x-3\right)\left(x+1\right)\)
\(\Rightarrow\left[{}\begin{matrix}x\ne2\\x-3\ne0\\x+1\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ne2\\x\ne3\\x\ne-1\end{matrix}\right.\)
Vậy \(ĐKXĐ\) là :\(x\ne2;3;-1\)
+ Pt thứ hai :
Ta có mẫu thức chung là : \(\left(x-2\right)\left(x+3\right)\)
\(\Rightarrow\left[{}\begin{matrix}x-2\ne0\\x+3\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ne2\\x\ne-3\end{matrix}\right.\)
Vậy \(DKXD:\) \(\) \(x\ne2;-3\)
Chọn chữ cái đứng trước câu trả lời đúng cho mỗi câu hỏi dưới đây
Câu 1: Điều kiện xác định của phương trình \(\dfrac{x-2}{x\left(x-2\right)}=0\) là:
A. \(x\ne0\) B. \(x\ne2\) C. \(x\ne0;x\ne-2\) D. \(x\ne0;x\ne2\)
Câu 2: Trong các phương trình sau phương trình nào là phương trình bậc nhất 1 ẩn?
A. x + \(x^2\)= 0
B. 1 -2x = 0
C. 0x + 4 = 0
D. \(\dfrac{1}{x-2}=0\)
Câu 3: Trong các cặp phương trình sau, cặp nào là 2 phương trình tương đương?
A. 3x-3 và x-1=0
B. x-3=0 và 3x+9=0
C. x-2=0 và (x-2)(x+3)=0
D. \(x^2+2=0vàx\left(x^2+2\right)=0\)
Câu 4: Trong các khẳng định sau, khẳng định nào đúng?
A) A(x) + B(x) = 0 \(\Leftrightarrow\)A(x) = 0 và B(x) = 0
B) A(x) . B(x) = 0 \(\Leftrightarrow\)A(x) = 0 và B(x) = 0
C) A(x) . B(x) = 0 \(\Leftrightarrow\)A(x) = 0 hoặc B(x) = 0
D) A(x) : B(x) = 0 \(\Leftrightarrow\)A(x) = 0 và B(x) = 0
Câu 5: Cho AB = 1,5 dm; CD = 30 cm. Tỉ số của hai đoạn thẳng AB và CD là:
A. \(\dfrac{1,5}{30}\) B. \(\dfrac{30}{1,5}\) C. 2 D. \(\dfrac{1}{2}\)
Câu 7: Cho \(\Delta\)ABC có AB =6cm ; AC = 8 cm; AD là phân giác trong \(\left(D\in BC\right)\). Hãy chọn đáp án đúng
A. \(\dfrac{BD}{DC}=\dfrac{4}{5}\) B. \(\dfrac{DB}{DC}=\dfrac{5}{3}\) C. \(\dfrac{DB}{DC}=\dfrac{3}{4}\) D. \(\dfrac{DB}{DC}=\dfrac{4}{3}\)
Câu 8: Cho hình vẽ sau, biết MN // QR. Độ dài x của đoạn thẳng QR có giá trị là:
A. x = 3 B. x = 4 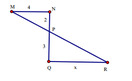
C. x = 5 D. x = 6
Câu 1: D
Câu 2: B
Câu 3: D
Câu 4: C
Câu 5: A
tìm điều kiện xác định của các phương trình sau
\(a,3x^2-2x=0\) \(b,\dfrac{1}{x-1}=3\)
\(c,\dfrac{2}{x-1}=\dfrac{x}{2x-4}\) \(d,\dfrac{2x}{x^2-9}=\dfrac{1}{x+3}\)
\(e,2x=\dfrac{1}{x^2-2x+1}\) \(f,\dfrac{1}{x-2}=\dfrac{2x}{x^2-5x+6}\)
giúp mik với , mik cần gấp
a)\(x\in R\)
b)\(x\ne1\)
c) \(x\notin\left\{1;2\right\}\)
d) \(x\notin\left\{3;-3\right\}\)
e) \(x\ne1\)
f) \(x\notin\left\{2;3\right\}\)
a) x∈R
b) x≠1
c) x∉{1;2}
d) x∉{3;−3}
e) x≠1
f) x∉{2;3}
Điều kiện xác định của phương trình \(\dfrac{2x+1}{x-1}+\dfrac{2-3x}{1+x}=\dfrac{1}{2}\)
Điều kiện xác định của phương trình : \(\dfrac{x}{x-2}-\dfrac{2x}{x^2-1}=0\) là :
\(A.x\ne-1;x\ne-2\)
\(B.x\ne2\) và \(x\ne\pm1\)
\(C.x\ne0\)
\(D.x\ne-2,x\ne1\)
để pt được xác định thì :
\(x-2\ne0;x^2-1\ne0\)
=>\(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne1\end{matrix}\right.\)
Vậy chọn B
Cho biểu thức: P =(\(\dfrac{x+2}{3x}+\dfrac{2}{x+1}-3\)) : \(\dfrac{2-4x}{x+1}-\dfrac{3x-x^2+1}{3x}\)
a) Tìm điều kiện xác định của P
b) Rút gọn biểu thức P
c) Tính giá trị của M với \(\left|2x-5\right|=5\)
d) Với giá trị nào của x thì P = \(\dfrac{-1}{2}\)
e) Tìm các giá trị của x để M \(\ge-1\)
f) Tìm các giá trị x nguyên để \(\dfrac{1}{M}\) nhận giá trị nguyên
Điều kiện xác định của phương trình là:\(\dfrac{2x+1}{x\left(x+1\right)}=2\) có phải x khác 0, và x khác -1 không ạ
bài 3cho biểu thức :A= \(\left[\dfrac{x}{x+3}+\dfrac{6x+9}{x\left(x+3\right)}\right]:\dfrac{x+3}{2}\)
a,tìm điều kiện xác định của biểu thức.
b,rút gọn biểu thức A.
c,tính giá trị của A khi x=\(\dfrac{1}{5}\)
a: ĐKXĐ: x<>0; x<>-3
b: \(=\dfrac{x^2+6x+9}{x\left(x+3\right)}\cdot\dfrac{2}{x+3}=\dfrac{2}{x}\)
c: Khi x=1/5 thì A=2:1/5=10
Câu 4: Cho biểu thức: \(A=\left(\dfrac{1}{\sqrt{x}-3}+\dfrac{1}{\sqrt{x}+3}\right)\left(1-\dfrac{3}{\sqrt{x}}\right)\)
a. Tìm điều kiện xác định của biểu thức A
b. Rút gọn A
c. Tìm x để giá trị biểu thức A > \(\dfrac{2}{5}\)
\(a,ĐK:x>0;x\ne9\\ b,A=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ A=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\\ c,A>\dfrac{2}{5}\Leftrightarrow\dfrac{2}{\sqrt{x}+3}-\dfrac{2}{5}>0\\ \Leftrightarrow\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{5}>0\\ \Leftrightarrow\dfrac{2-\sqrt{x}}{5\left(\sqrt{x}+3\right)}>0\\ \Leftrightarrow2-\sqrt{x}>0\left(\sqrt{x}+3>0\right)\\ \Leftrightarrow\sqrt{x}< 2\Leftrightarrow0< x< 4\)