Giải bất phương trình sau và biểu diễn nghiệm trên trục số
X-2/6-x-1/6
Giải bất phương trình sau và biểu diễn nghiệm trên trục số
x-2/6 - x-1/3 < x/2
`(x-2)/6 -(x-1)/3 < x/2`
`<=> (x-2)/6 -(2(x-1))/6 < (3x)/6`
`<=> x-2 - (2x-2) <3x`
`<=> x-2-2x+2<3x`
`<=> -x <3x`
`<=> -x-3x<0`
`<=> -4x<0`
`<=> x>0`
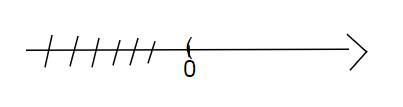
\(\dfrac{x-2}{6}\)-\(\dfrac{x-1}{3}\)<\(\dfrac{x}{2}\)
\(\dfrac{x-2}{6}\)-\(\dfrac{2\left(x-1\right)}{6}\)<\(\dfrac{6x}{6}\)
<=>x-2-2x+2<6x
<=>-7x<0
<=>x>0
vậy tập nghiệm của bất phương trình là
\(\left\{x|x>0\right\}\)
\(\dfrac{x-2}{6}-\dfrac{x-1}{3}< \dfrac{x}{2}\\ \Leftrightarrow\dfrac{x-2}{6}-\dfrac{\left(x-1\right)2}{3.2}< \dfrac{x.3}{2.3}\\ \Leftrightarrow x-2-2x+2< 3x\\ \Leftrightarrow x-2x-3x< -2\\ \Leftrightarrow-4x< -2\\ \Leftrightarrow x>\dfrac{1}{2}\)
Vậy bất phương trình có tập nghiệm là:
\(S=\left\{x|x>\dfrac{1}{2}\right\}\)
Biểu diễn:
giải bất phương trình sau và biểu diễn trên trục số
x\(-\)5 \(\ge\) 8\(-\)3x
x\(-\)3 < x\(-\)5
Giải :
\(x-5\ge8-3x\\ \Leftrightarrow x+3x\ge8+5\\ \Leftrightarrow4x\ge13\\ \Leftrightarrow x\ge\dfrac{13}{4}\)
Biểu diễn :
b,
\(x-3< x-5\\ \Leftrightarrow-3< -5\left(voli\right)\)
giải bất phương trình sau và biểu diễn tập nghiệm trên trục số x + 3 > 6
\(x+3>6\)
\(\Leftrightarrow x>6-3\)
\(\Leftrightarrow x>3\)
Biểu diễn trên trục số:
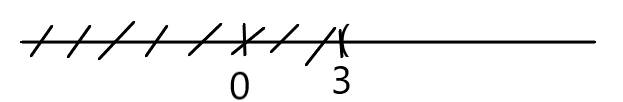
Giải bất phương trình sau và biểu diễn nghiệm trên trục số 6 - 4 x 6 < 1
Ta có: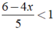 ⇔ 6 - 4x < 5
⇔ 6 - 4x < 5
⇔ 4x > 1 ⇔ x > 1/4
Vậy x > 1/4 là nghiệm của bất phương trình đã cho.
Ta biểu diễn tập nghiệm trên trục số như sau:
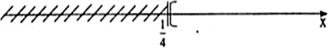
giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số
\(\dfrac{x-1}{3}\)-\(\dfrac{3x+5}{2}\)≥1-\(\dfrac{4x+5}{6}\)
Ta có: \(\dfrac{x-1}{3}-\dfrac{3x+5}{2}\ge1-\dfrac{4x+5}{6}\)
\(\Leftrightarrow2\left(x-1\right)-3\left(3x+5\right)\ge6-4x-5\)
\(\Leftrightarrow2x-2-9x-15-6+4x+5\ge0\)
\(\Leftrightarrow-3x\ge18\)
hay \(x\le-6\)
2. Giải bất phương trình và biểu diễn tập nghiệm trên trục số
a) \(3x-2\ge x+6\)
b) (\(3x-6\)) \(-\left(-2x-1\right)\)\(\ge0\)
a)3x-2≥x+6
<=>3x-x≥6+2
<=>2x≥8
<=>x≥4
tập nghiệm của phương trình là
\(S=\left\{xIx\ge4\right\}\)
biểu diễn tập nghiệm trên trục số
b)(3x-6)-(-2x-1)≥0
<=>3x-6++1≥0
<=>3x+2x≥6-1
<=>5x≥5
<=>x≥1
tập nghiệm của phương trình là
\(S=\left\{xIx\ge1\right\}\)
a: =>2x>=8
=>x>=4
b: =>3x-6+2x+1>=0
=>5x-5>=0
=>x>=1
a) giải phương trình: 8x-3=5x+12
b) giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\dfrac{8-11x}{4}\)< 13
c) Chứng minh rằng: (\(\dfrac{x}{x^2-36}\)- \(\dfrac{x-6}{x^2+6x}\)): \(\dfrac{2x-6}{x^2+6x}\)+ \(\dfrac{x}{6-x}\)= 1
a:=>3x=15
=>x=5
b: =>8-11x<52
=>-11x<44
=>x>-4
c: \(VT=\left(\dfrac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2x-6}+\dfrac{x}{6-x}\)
\(=\dfrac{12x-36}{2x-6}\cdot\dfrac{1}{x-6}-\dfrac{x}{x-6}=\dfrac{6}{x-6}-\dfrac{x}{x-6}=-1\)
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 3 x + 7 > x + 5 b) x−4≤−3x+6.
giải bất phương trình sau và biểu diễn nghiệm trên trục số a)5x+6>2x+3 b)4x+1<2x-9
\(2x+2x+1< 2x-9\)
\(\Leftrightarrow2x+1< -9\)
\(\Leftrightarrow2x< 9-1\Leftrightarrow2x< 8\)
\(\Leftrightarrow2x:2< 8:2\Leftrightarrow x< 4\)
\(4x+1< 2x-9\)
\(\Leftrightarrow4x+1-2x+9< 0\)
\(\Leftrightarrow2x+10< 0\)
\(\Leftrightarrow2x< -10\)
\(\Leftrightarrow x< -5\)