giúp mình câu a,b

giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
mình mình  mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
ảnh kia nhiều người lắm like thế :)
các bạn giúp mình câu a và câu b với mình cảm ơn trước
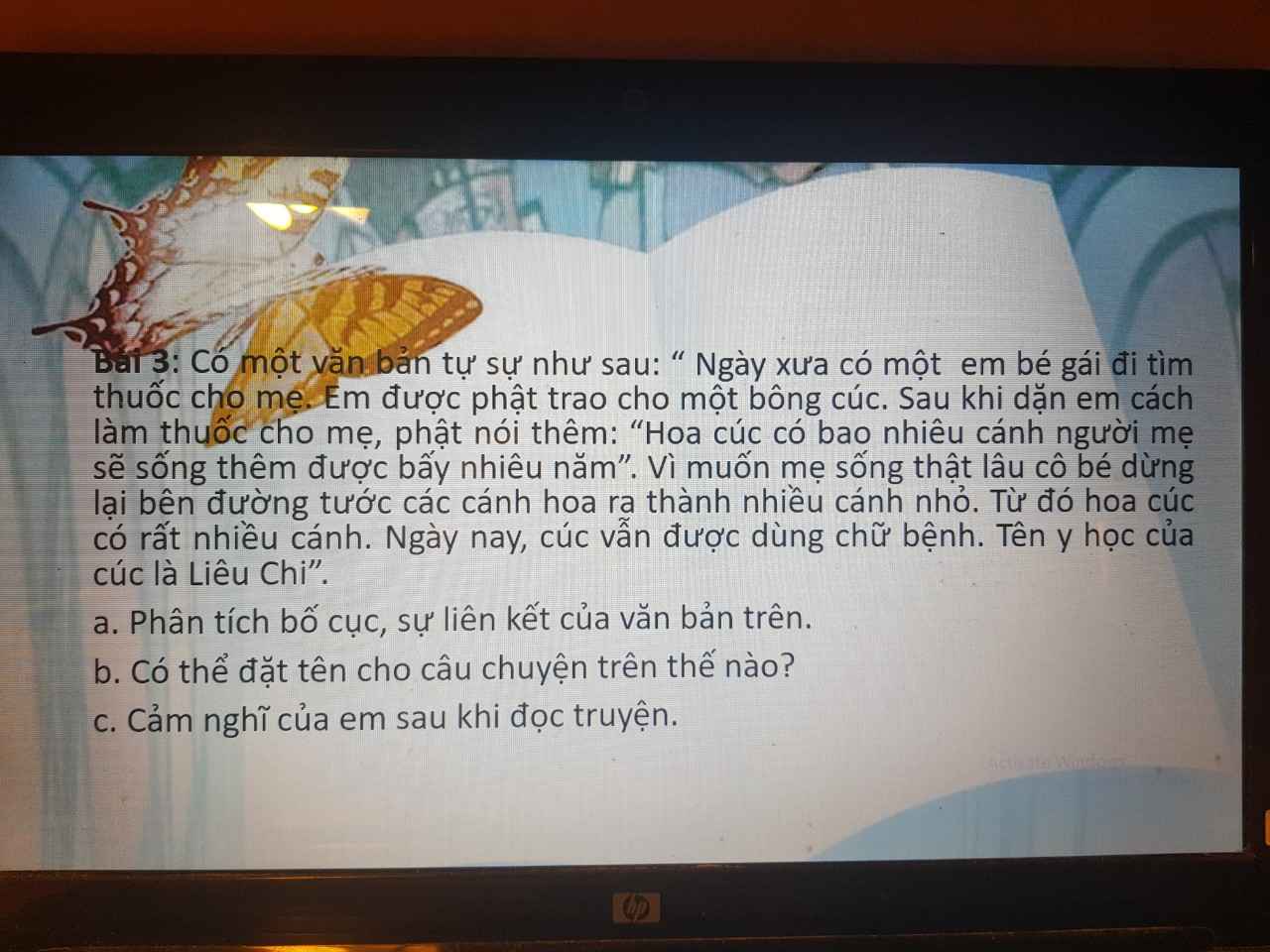
Mong các bạn giải giúp mình câu b với ạ! ( câu b mình làm không đúng đâu )
Còn câu a là thầy giáo mình đã chữa.
Cảm ơn các bạn nhiều ạ !!!


 Giúp mình câu a b c nếu được thì câu d
Giúp mình câu a b c nếu được thì câu d
a.
\(O=AC\cap BD\Rightarrow O\in BD\in\left(SBD\right)\) \(\Rightarrow SO\in\left(SBD\right)\)
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\Rightarrow AC\perp SD\)
b.
O là trung điểm AC, H là trung điểm AB \(\Rightarrow\) OH là đường trung bình tam giác ABC
\(\Rightarrow OH||BC\Rightarrow OH\perp AB\Rightarrow OH\perp CD\) (1)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SHO\right)\)
c.
Theo cmt trên \(OH||BC\Rightarrow OH||AD\)
\(\Rightarrow\widehat{\left(OH;SD\right)}=\widehat{\left(AD;SD\right)}=\widehat{SDA}\)
\(AC=2a\sqrt{2}\Rightarrow OA=a\sqrt{2}\Rightarrow SA=SB=SC=SD=\sqrt{SO^2+OA^2}=a\sqrt{3}\)
Áp dụng định lý hàm cosin trong tam giác SAD:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\widehat{SDA}=...\)
d.
Gọi E là trung điểm SB \(\Rightarrow HE\) là đường trung bình tam giác SAB
\(\Rightarrow HE||SA\Rightarrow\widehat{\left(HK;SA\right)}=\widehat{\left(HK;HE\right)}=\widehat{KHE}\)
\(SK=\dfrac{1}{3}SC=\dfrac{a\sqrt{3}}{3}\) ; \(SE=\dfrac{1}{2}SB=\dfrac{a\sqrt{3}}{2}\) ; \(EH=\dfrac{1}{2}SA=\dfrac{a\sqrt{3}}{2}\)
\(cos\widehat{BSC}=\dfrac{SB^2+SC^2-BC^2}{2SB.SC}=\dfrac{1}{3}\)
\(\Rightarrow EK=\sqrt{SE^2+SK^2-2SE.SK.cos\widehat{BSC}}=\dfrac{a\sqrt{3}}{2}\)
Từ K kẻ KF song song SO \(\Rightarrow KF\perp\left(ABCD\right)\Rightarrow KF\perp HF\)
\(\dfrac{KF}{SO}=\dfrac{CK}{CS}=\dfrac{2}{3}\Rightarrow KF=\dfrac{2a}{3}\)
\(\dfrac{OF}{OC}=\dfrac{SK}{SC}=\dfrac{1}{3}\Rightarrow OF=\dfrac{1}{3}OC\Rightarrow AF=\dfrac{4}{3}OC=\dfrac{2}{3}AC=\dfrac{4a\sqrt{2}}{3}\)
\(\Rightarrow HF=\sqrt{AH^2+AF^2-2AH.AF.cos45^0}=\dfrac{a\sqrt{17}}{3}\)
\(\Rightarrow HK=\sqrt{HF^2+KF^2}=\dfrac{a\sqrt{21}}{3}\)
\(\Rightarrow cos\widehat{KHE}=\dfrac{HK^2+EH^2-EK^2}{2HK.EH}=\dfrac{\sqrt{7}}{3}\)
Giúp mình câu a,b với
a: Xét tứ giác ABMC có
D là trung điểm của AM
D là trung điểm của BC
Do đó: ABMC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABMC là hình chữ nhật
Bài 3:
a. Vì D là trung điểm AM và BC nên ABMC là hình bình hành
b. Vì D,E là trung điểm BC,AB nên DE là đtb \(\Delta ABC\)
Do đó \(DE//AB\Rightarrow DE\bot AC\)
Vì D,F là trung điểm BC,AC nên DF là đtb \(\Delta ABC\)
Do đó \(DF//AC\Rightarrow DF\bot AB\)
Từ đây ta được AEDF là hình chữ nhật
Vậy \(AD=EF\)
c. Vì E là trung điểm AB và DK nên ADBK là hình bình hành
Lại có \(AB\bot DK\) nên ADBK là hình thoi
d. Để AEDF là hình vuông thì \(AF=FD\)
Mà \(AF=\dfrac{1}{2}AC,DF=\dfrac{1}{2}AB\)
\(\Leftrightarrow AC=AB\Leftrightarrow\Delta ABC\) vuông cân tại A
Vậy để AEDF là hình vuông thì \(\Delta ABC\) vuông cân tại A
Giúp mình câu A,B,C (Đề 24) . Mình đang cần gấp 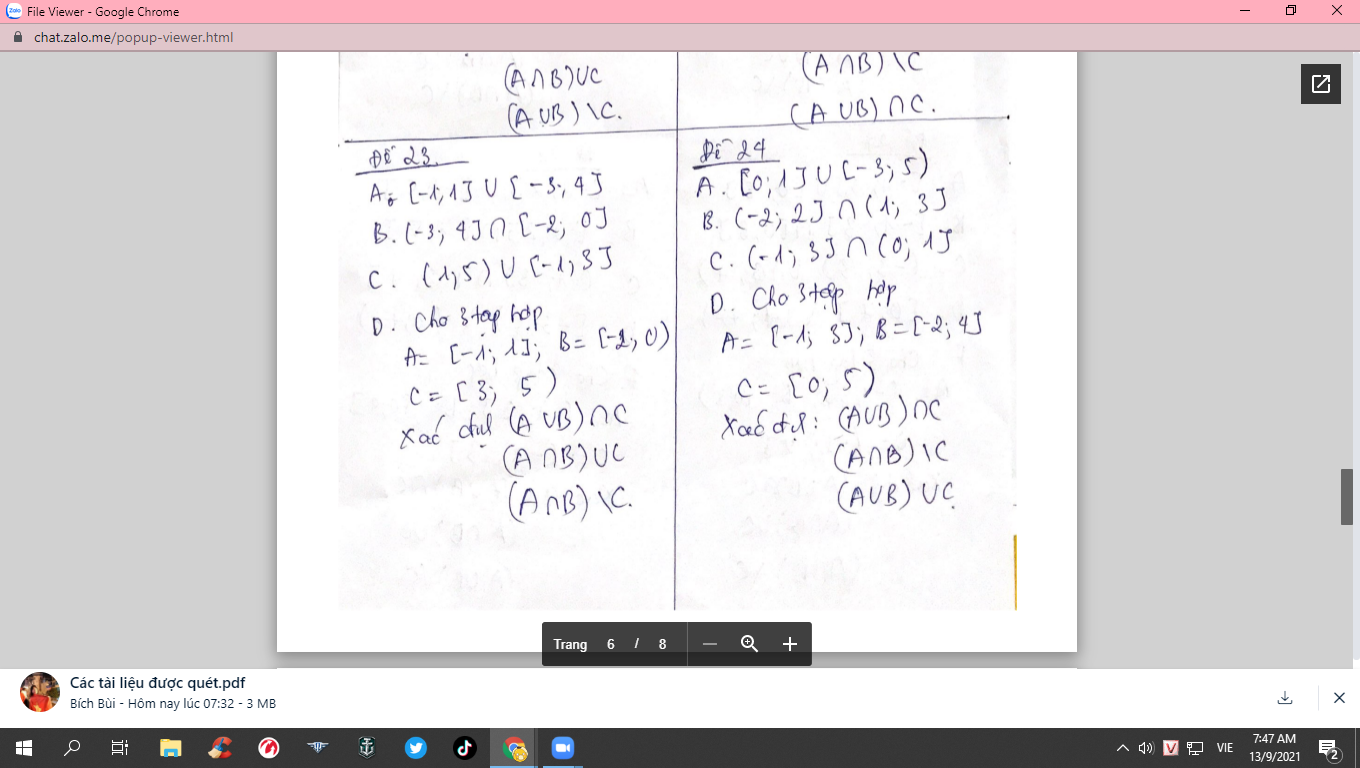
\(a,A=\left\{-3;-2;-1;0;1;2;3;4\right\}\\ b,B=\left\{2\right\}\\ c,C=\left\{1\right\}\\ d,\left(A\cup B\right)\cap C=\left\{0;1;2;3;4\right\}\\ \left(A\cap B\right)\ C=\left\{-1\right\}\\ \left(A\cup B\right)\cup C=\left\{-2;-1;0;1;2;3;4\right\}\)
 giúp mình câu a, b với ạ
giúp mình câu a, b với ạ
b) Thay y=0 vào (d1), ta được:
\(\dfrac{1}{2}x+2=0\)
\(\Leftrightarrow x\cdot\dfrac{1}{2}=-2\)
hay x=-4
Vậy: A(-4;0)
Thay y=0 vào (d2), ta được:
\(2-x=0\)
hay x=2
Vậy: B(2;0)
Phương trình hoành độ giao điểm của (d1) và (d2) là:
\(\dfrac{1}{2}x+2=-x+2\)
\(\Leftrightarrow x=0\)
Thay x=0 vào (d2), ta được:
\(y=-0+2=2\)
Vậy: C(0;2)
\(AB=\sqrt{\left(-4-2\right)^2+\left(0-0\right)^2}=6\)
\(AC=\sqrt{\left(-4-0\right)^2+\left(0-2\right)^2}=2\sqrt{5}\)
\(BC=\sqrt{\left(2-0\right)^2+\left(0-2\right)^2}=2\sqrt{2}\)
c) Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=6+2\sqrt{5}+2\sqrt{2}\left(cm\right)\)
\(\Leftrightarrow P_{ABC}=\dfrac{C_{ABC}}{2}=3+\sqrt{5}+\sqrt{2}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\sqrt{P\cdot\left(P-AB\right)\left(P-AC\right)\left(P-BC\right)}\)
\(=\sqrt{\left(3+\sqrt{5}+\sqrt{2}\right)\left(-3+\sqrt{5}+\sqrt{2}\right)\left(3-\sqrt{5}+\sqrt{2}\right)\left(3+\sqrt{5}-\sqrt{2}\right)}\)
\(=6\left(cm^2\right)\)
Giúp mình câu a, b với ạ!

a:Thay x=1 và y=-1 vào (d), ta được:
2a-4=-1
hay \(a=\dfrac{3}{2}\)
a) Ta có: \(A\left(1;-1\right)\in\left(d\right)\Rightarrow y_A=\left(2a-1\right)x_A-3\)
\(\Rightarrow-1=\left(2a-1\right).1-3\Rightarrow2a-1=2\)
Vậy \(\left(d\right):y=2x-3\)
b) Ta có: \(\left(d'\right)\perp\left(d\right)\Leftrightarrow a.a'=-1\)
\(\Leftrightarrow a'.2=-1\Leftrightarrow a'=-\dfrac{1}{2}\Leftrightarrow\left(d'\right):y=-\dfrac{1}{2}x+b\)
Ta có: \(\left(d'\right)\) cắt trục tung tại điểm B có tung độ là \(\dfrac{4}{3}\)
\(\Leftrightarrow b=\dfrac{4}{3}\)
Vậy \(\left(d'\right):y=-\dfrac{1}{2}x+\dfrac{4}{3}\)
a, Vì (d) đi qua A(1;-1) nên \(x=1;y=-1\)
\(\Leftrightarrow2a-1-3=-1\\ \Leftrightarrow a=\dfrac{3}{2}\)
Vậy \(\left(d\right):y=\left(2\cdot\dfrac{3}{2}-1\right)x-3=2x-3\)
\(b,\) Gọi \(\left(d'\right):y=cx+d\left(c\ne0\right)\) là đt cần tìm
\(\left(d'\right)\perp\left(d\right)\Leftrightarrow2c=-1\Leftrightarrow c=-\dfrac{1}{2}\)
\(\left(d'\right)\) cắt trục tung tại điểm B có tung độ \(\dfrac{4}{3}\Leftrightarrow x=0;y=\dfrac{4}{3}\Leftrightarrow d=\dfrac{4}{3}\)
Vậy \(\left(d'\right):y=-\dfrac{1}{2}x+\dfrac{4}{3}\)
c, PTHDGD của \(\left(d\right)\) và \(\left(d'\right)\) là \(-\dfrac{1}{2}x+\dfrac{4}{3}=2x-3\Leftrightarrow\dfrac{5}{2}x=\dfrac{13}{3}\Leftrightarrow x=\dfrac{26}{15}\\ \Leftrightarrow y=\dfrac{7}{15}\Leftrightarrow C\left(\dfrac{26}{15};\dfrac{7}{15}\right)\)
d, Ta có \(B\left(0;\dfrac{4}{3}\right)\Leftrightarrow BC=\sqrt{\left(\dfrac{26}{15}-0\right)^2+\left(\dfrac{7}{15}-\dfrac{4}{3}\right)^2}=\dfrac{13\sqrt{5}}{15}\)
\(AC=\sqrt{\left(\dfrac{26}{15}-1\right)^2+\left(\dfrac{7}{15}+1\right)^2}=\dfrac{11\sqrt{5}}{15}\)
Vì \(\Delta ABC\) vuông tại C nên \(S_{ABC}=\dfrac{1}{2}AC\cdot BC=\dfrac{1}{2}\cdot\dfrac{13\sqrt{5}}{15}\cdot\dfrac{11\sqrt{5}}{15}=\dfrac{143}{90}\left(đvdt\right)\)