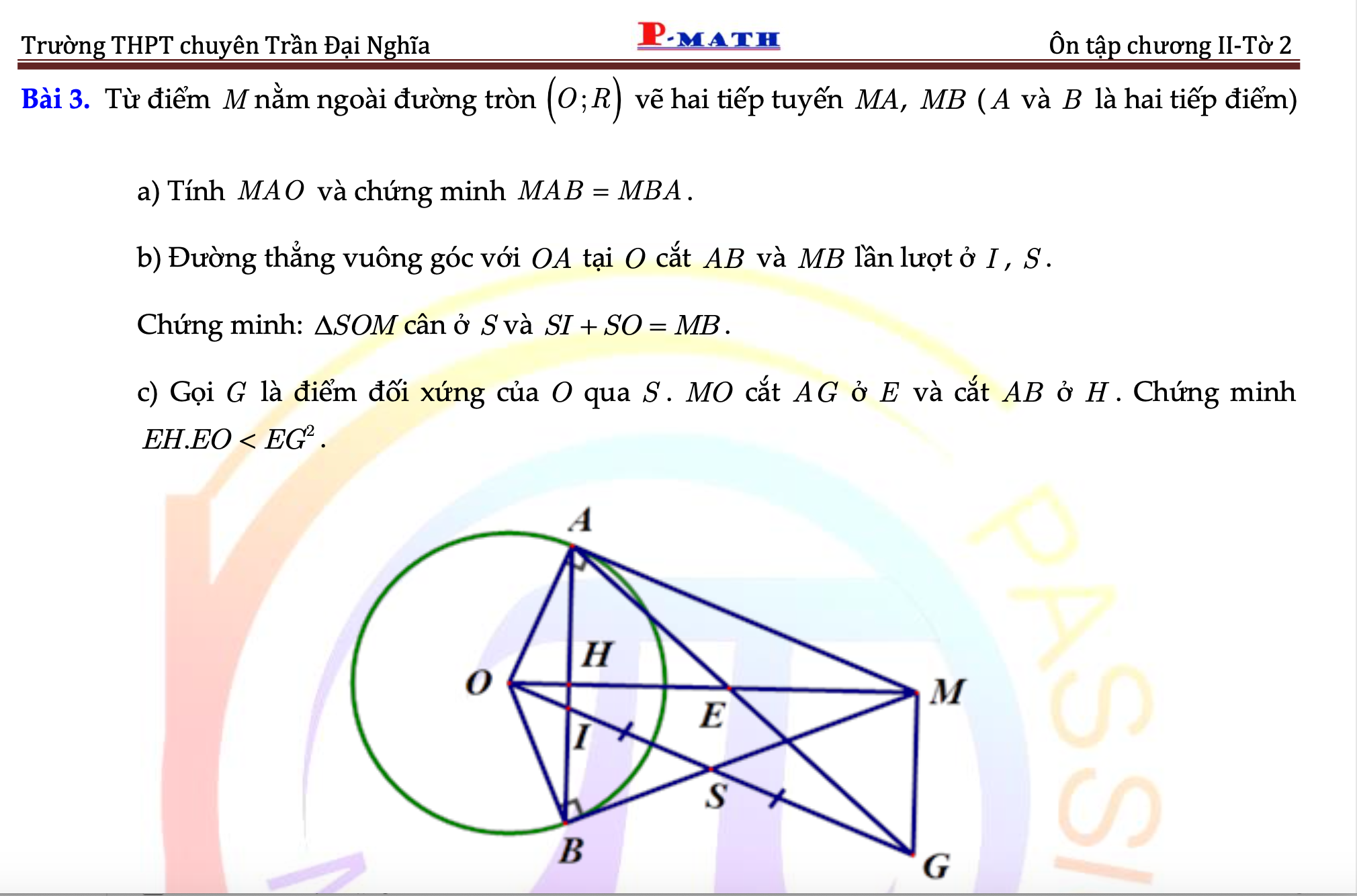
a:Thay x=1 và y=-1 vào (d), ta được:
2a-4=-1
hay \(a=\dfrac{3}{2}\)
a) Ta có: \(A\left(1;-1\right)\in\left(d\right)\Rightarrow y_A=\left(2a-1\right)x_A-3\)
\(\Rightarrow-1=\left(2a-1\right).1-3\Rightarrow2a-1=2\)
Vậy \(\left(d\right):y=2x-3\)
b) Ta có: \(\left(d'\right)\perp\left(d\right)\Leftrightarrow a.a'=-1\)
\(\Leftrightarrow a'.2=-1\Leftrightarrow a'=-\dfrac{1}{2}\Leftrightarrow\left(d'\right):y=-\dfrac{1}{2}x+b\)
Ta có: \(\left(d'\right)\) cắt trục tung tại điểm B có tung độ là \(\dfrac{4}{3}\)
\(\Leftrightarrow b=\dfrac{4}{3}\)
Vậy \(\left(d'\right):y=-\dfrac{1}{2}x+\dfrac{4}{3}\)
a, Vì (d) đi qua A(1;-1) nên \(x=1;y=-1\)
\(\Leftrightarrow2a-1-3=-1\\ \Leftrightarrow a=\dfrac{3}{2}\)
Vậy \(\left(d\right):y=\left(2\cdot\dfrac{3}{2}-1\right)x-3=2x-3\)
\(b,\) Gọi \(\left(d'\right):y=cx+d\left(c\ne0\right)\) là đt cần tìm
\(\left(d'\right)\perp\left(d\right)\Leftrightarrow2c=-1\Leftrightarrow c=-\dfrac{1}{2}\)
\(\left(d'\right)\) cắt trục tung tại điểm B có tung độ \(\dfrac{4}{3}\Leftrightarrow x=0;y=\dfrac{4}{3}\Leftrightarrow d=\dfrac{4}{3}\)
Vậy \(\left(d'\right):y=-\dfrac{1}{2}x+\dfrac{4}{3}\)
c, PTHDGD của \(\left(d\right)\) và \(\left(d'\right)\) là \(-\dfrac{1}{2}x+\dfrac{4}{3}=2x-3\Leftrightarrow\dfrac{5}{2}x=\dfrac{13}{3}\Leftrightarrow x=\dfrac{26}{15}\\ \Leftrightarrow y=\dfrac{7}{15}\Leftrightarrow C\left(\dfrac{26}{15};\dfrac{7}{15}\right)\)
d, Ta có \(B\left(0;\dfrac{4}{3}\right)\Leftrightarrow BC=\sqrt{\left(\dfrac{26}{15}-0\right)^2+\left(\dfrac{7}{15}-\dfrac{4}{3}\right)^2}=\dfrac{13\sqrt{5}}{15}\)
\(AC=\sqrt{\left(\dfrac{26}{15}-1\right)^2+\left(\dfrac{7}{15}+1\right)^2}=\dfrac{11\sqrt{5}}{15}\)
Vì \(\Delta ABC\) vuông tại C nên \(S_{ABC}=\dfrac{1}{2}AC\cdot BC=\dfrac{1}{2}\cdot\dfrac{13\sqrt{5}}{15}\cdot\dfrac{11\sqrt{5}}{15}=\dfrac{143}{90}\left(đvdt\right)\)
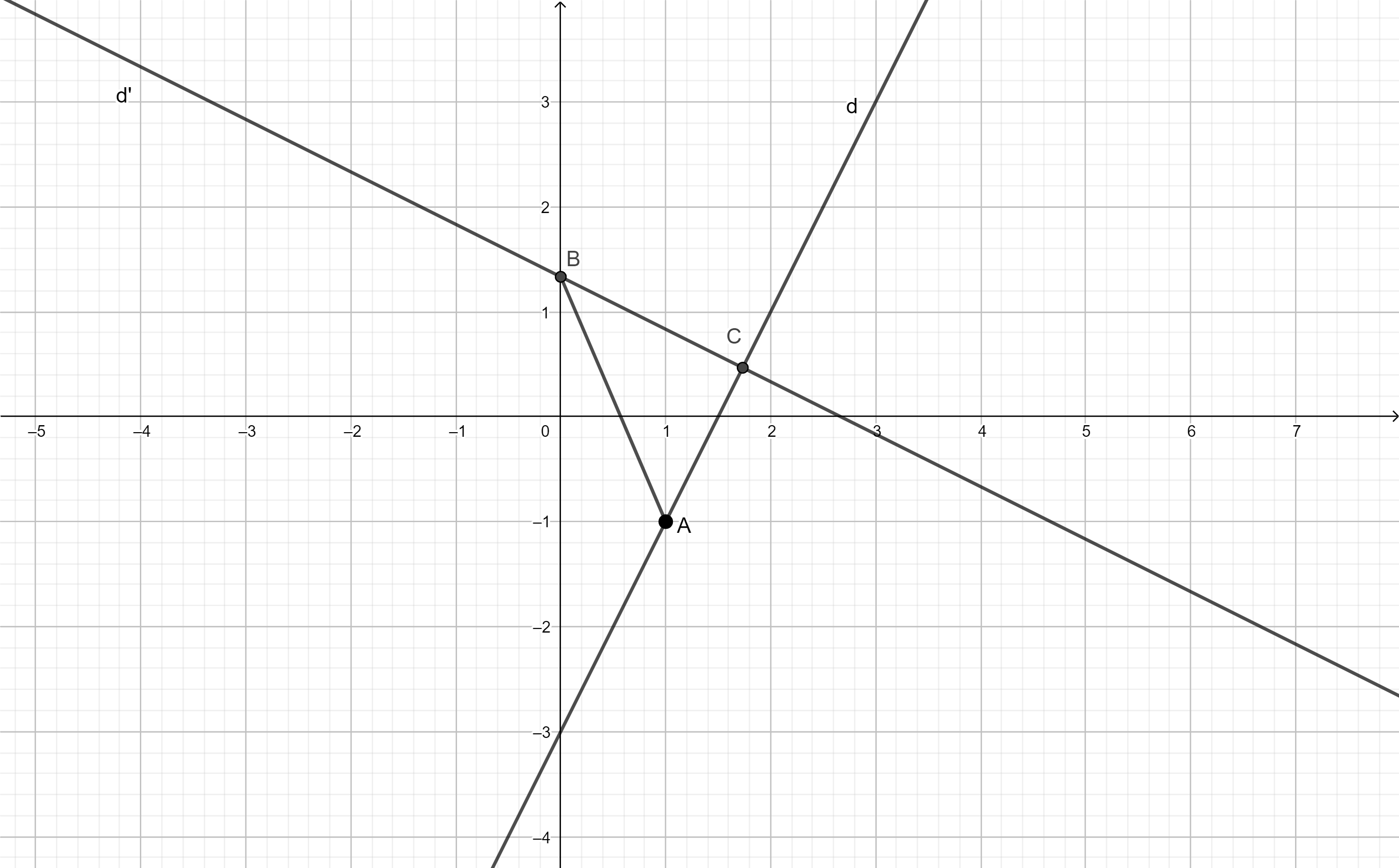
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 
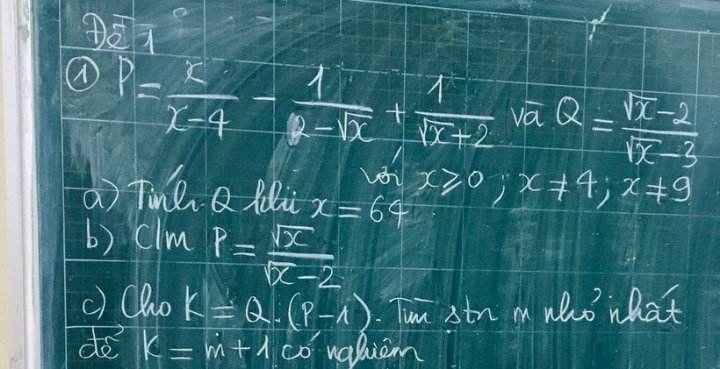giúp mình câu c với ạ, mình cảm ơn nhiều