a: Xét (O) có
MA là tiếp tuyến có A là tiếp điểm
MB là tiếp tuyến có B là tiếp điểm
Do đó: MA=MB
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
hay \(\widehat{MAB}=\widehat{MBA}\)
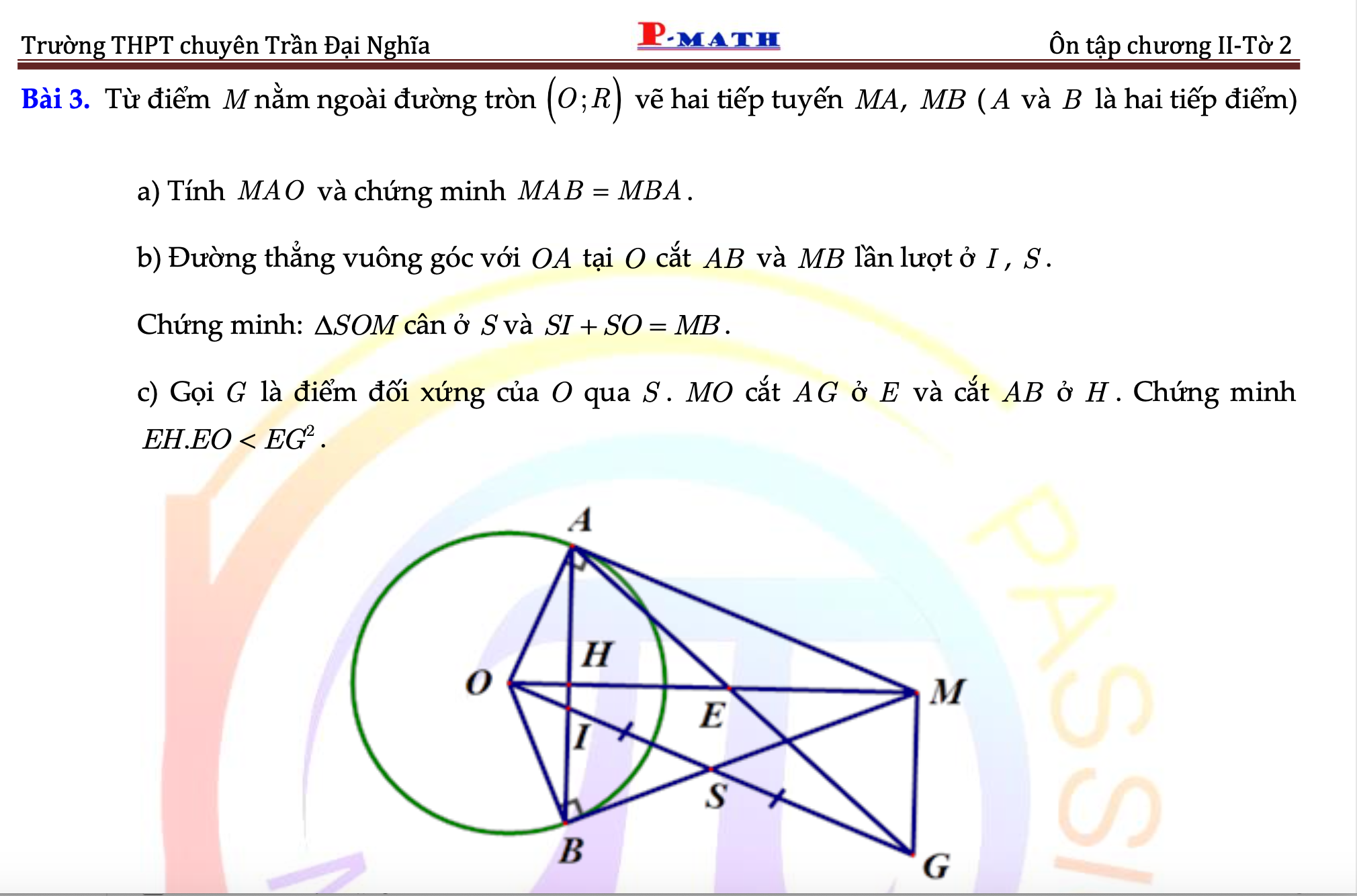
c, Vì \(AM=MB\Rightarrow M\in\) trung trực AB
Vì \(OA=OB=R\Rightarrow O\in\) trung trực AB
Do đó OM là trung trực AB
\(\Rightarrow OM\perp AB\) tại H
Mà SO=OM (SOM cân) và \(SO=\dfrac{1}{2}OG\)(S là trung điểm)
Do đó \(SM=\dfrac{1}{2}OG\) hay \(\Delta OMG\) vuông tại M
\(\Rightarrow AH//MG\left(\perp MO\right)\)
Áp dụng Talet: \(\left\{{}\begin{matrix}\dfrac{EG}{EA}=\dfrac{EM}{EH}\\\dfrac{EG}{EA}=\dfrac{EO}{EM}\end{matrix}\right.\Rightarrow\dfrac{EM}{EH}=\dfrac{EO}{EM}\Rightarrow EO\cdot EH=EM^2\)
Mà \(\Delta EMG\perp M\) nên \(EM< EG\) (EG là cạnh huyền)
Vậy \(EO\cdot EH< EG^2\)







 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 

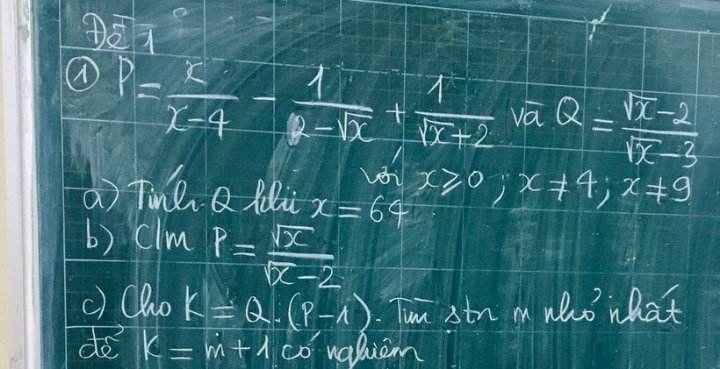 giúp mình câu c với ạ, mình cảm ơn nhiều
giúp mình câu c với ạ, mình cảm ơn nhiều











