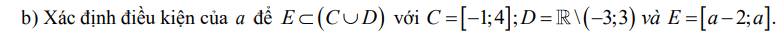lớp 10a có 45 học sinh, 21 giỏi toán, 22 giỏi lí, 20 giỏi hóa. hỏi có bao nhiêu hs giỏi đúng 1 môn biết 12 bạn k giỏi môn nào ?
§3. Các phép toán tập hợp
Cho A=(2,5] ; B=[-3,6).Tìm hợp của hai tập hợp A và B
A=(2;5]
B=[-3;6)
=>\(A\cup B=[-3;6)\)
Đúng 0
Bình luận (0)
\(C=[-1;4]\)
\(D=R\)\\(\left(-3;3\right)\)
\(E=\left[a-2;a\right]\)
\(\Rightarrow C\cup D=(-\infty;-3)\cup[-1;+\infty)\)
\(E\subset\left(C\cup D\right)\Leftrightarrow\left[{}\begin{matrix}a< -3\\a-2\ge-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}a< -3\\a\ge1\end{matrix}\right.\)
Vậy \(a< -3\cup a\ge1\) thỏa mãn yêu cầu đề bài.
Đúng 0
Bình luận (0)
Câu 2: D
Câu 3: B
Câu 4: C
Câu 5: C
Câu 6: D
Câu 7: B
Câu 8: D
Câu 9: B
Đúng 0
Bình luận (0)
Câu 2: D
Câu 3: B
Câu 4: C
Câu 5: C
Câu 6: D
Câu 7: B
Câu 8: D
Câu 9: B
Đúng 0
Bình luận (0)
Giúp mình câu 6 với mng
Cho tập A = [m+1; m+2] và tập B = [0;1]. Tìm các giá trị thực của m sao cho A ∩ B = Ø
Mọi người ơi giúp e với e dang gấp, e cảm ơn ạ :<
\(A\cap B\\ \Leftrightarrow\left\{{}\begin{matrix}m+2< 0\\m+1< 1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m< 0\end{matrix}\right.\\ hay.m\in\left[-\infty;-1\right]\cap\left[1;+\infty\right]\)
Đúng 1
Bình luận (0)
Số giá trị nguyên của tham số m để phương trình x^4 -2mx^2+9=0 có bốn nghiệm phân biệt nhỏ hơn hoặc bằng 3 là
Cho tập A={x thuộc Z|x^2/2x+3 thuộc Z} số tập con của A là
giúp em với ạ
11B
A={0;2;3;5}
B={2;7}
=>\(A\cap B=\left\{2\right\}\)
10
\(X=\left\{1;2;4;7;9\right\};Y=\left\{-1;0;7;10\right\}\)
=>\(X\cup Y=\left\{1;2;4;7;9;-1;0;10\right\}\)
=>Chọn C
9:
\(A=\left\{a;b;c\right\};B=\left\{a;c;d;e\right\}\)
=>\(A\cap B=\left\{a;c\right\}\)
=>Chọn A
8C
7B nha bạn
Đúng 0
Bình luận (0)