Ôn tập chương I
Nội dung lý thuyết
1. Mệnh đề
- Mỗi mệnh đề phải hoặc đúng hoặc sai. Một mệnh đề không thể vừa đúng vừa sai.
Ví dụ: - Mệnh đề "\(x^2\ge0,\forall x\in R\)" là một mệnh đề đúng ;
- Mệnh đề "Phan-xi-păng là ngọn núi ở vùng Tây Nam Bộ" là một mệnh đề sai.
- Kí hiệu mệnh đề phủ định của mệnh đề \(P\) là \(\overline{P}\), ta có:
\(\overline{P}\) đúng khi \(P\) sai ;
\(\overline{P}\) sai khi \(P\) đúng.
Ví dụ: \(P\): "3 là một nguyên tố." (đúng)
\(\overline{P}\): "3 không phải là một số nguyên tố." (sai)
- Mệnh đề "Nếu \(P\) thì \(Q\)" được gọi là mệnh đề kéo theo, và được kí hiệu là \(P\Rightarrow Q\).
- Mệnh đề \(P\Rightarrow Q\) chỉ sai khi \(P\) đúng và \(Q\) sai.
- Các định lí toán học là các mệnh đề đúng và thường có dạng \(P\Rightarrow Q\). Khi đó ta nói:
\(P\) là giả thiết, \(Q\) là kết luận của định lí, hoặc
\(P\) là điều kiện đủ để có \(Q\), hoặc
\(Q\) là điều kiện cần để có \(P\).
- Mệnh đề \(Q\Rightarrow P\) được gọi là mệnh đề đảo của mệnh đề \(P\Rightarrow Q\).
Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
- Nếu cả 2 mệnh đề \(P\Rightarrow Q\) và \(Q\Rightarrow P\) đều đúng ta nói \(P\) và \(Q\) là hai mệnh đề tương đương. Khi đó ta kí hiệu là \(P\Leftrightarrow Q\) và đọc là
\(P\) tương đương \(Q\), hoặc
\(P\) là điều kiện cần và đủ để có \(Q\), hoặc
\(P\) khi và chỉ khi \(Q\).
Ví dụ: "Tam giác \(ABC\) cân và có một góc \(60^0\) là điều kiện cần và đủ để tam giác \(ABC\) đều."
- Kí hiệu \(\forall\) đọc là "với mọi"
Ví dụ: \(x^2\ge0,\forall x\in R\)
- Kí hiệu \(\exists\) đọc là "có một" (tồn tại một) hay "có ít nhất một" (tồn tại ít nhất một).
Ví dụ: \(\exists n\in Z:n^2=1\).
@70302@
2. Tập hợp
- Tập hợp (còn gọi là tập) là một khái niệm cơ bản của toán học, không định nghĩa.
- Giả sử đã cho tập hợp \(A\). Để chỉ \(a\) là một phần tử của tập hợp \(A\), ta viết \(a\in A\) (đọc là \(a\)thuộc \(A\)). Để chỉ \(a\) không phải là một phần tử của tập hợp \(A\) ta viết \(a\notin A\) (đọc là \(a\) không thuộc \(A\)).
- Ta có thể xác định tập hợp bằng một trong hai cách sau:
a) Liệt kê các phần tử của nó ;
b) Chỉ ra tính chất đặc trưng cho các phần tử của nó.
Ví dụ: \(A=\left\{0;2;4;6;8;10\right\}\)
\(A=\left\{x\in N|x⋮2,x\le10\right\}\)
- Ngoài ra, người ta có thể dùng biểu đồ Ven để minh hoạ một tập hợp.

- Tập hợp rỗng, kí hiệu là \(\varnothing\), là tập hợp không có phần tử nào.
- Nếu \(A\) không phải là tập hợp rỗng thì \(A\) chứa ít nhất một phần tử: \(A\ne\varnothing\Leftrightarrow\exists x:x\in A\)
- Nếu mọi phần tử của tập hợp \(A\) đều là phần tử của tập hợp \(B\) thì ta nói \(A\) là một tập hợp con của \(B\) và kí hiệu là \(A\subset B\) (đọc là \(A\) chứa trong \(B\)); hoặc \(B\supset A\) (đọc là \(B\) chứa \(A\)hoặc \(B\) bao hàm \(A\)).
\(A\subset B\Leftrightarrow\left(\forall x:x\in A\Rightarrow x\in B\right)\)
- Ta có các tính chất:
a) \(A\subset A\) với mọi tập hợp \(A\) ;
b) Nếu \(A\subset B\) và \(B\subset C\) thì \(A\subset C\) ;
c) \(\varnothing\subset A\) với mọi tập hợp \(A\).
- Khi \(A\subset B\) và \(B\subset A\) ta nói tập hợp \(A\) bằng tập hợp \(B\) và viết là \(A=B\).
\(A=B\Leftrightarrow\left(\forall x:x\in A\Leftrightarrow x\in B\right)\)
3. Các phép toán tập hợp
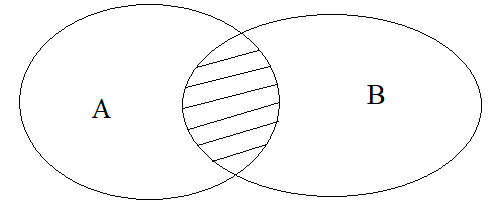
- Giao của hai tập hợp: Tập hợp \(C\) gồm các phần tử vừa thuộc \(A\) vừa thuộc \(B\) được gọi là giao của \(A\) và \(B\). Kí hiệu \(C=A\cap B\).
\(A\cap B=\left\{x|x\in A;x\in B\right\}\)
\(x\in A\cap B\Leftrightarrow\left\{{}\begin{matrix}x\in A\\x\in B\end{matrix}\right.\)
- Hợp của hai tập hợp: Tập hợp \(C\) gồm các phần tử thuộc \(A\) hoặc thuộc \(B\) được gọi là hợp của \(A\) và \(B\). Kí hiệu là \(C=A\cup B\).
\(A\cup B=\){\(x|x\in A\) hoặc \(x\in B\)}
\(x\in A\cup B\Leftrightarrow\left[{}\begin{matrix}x\in A\\x\in B\end{matrix}\right.\)

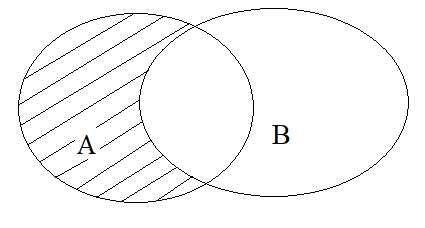
- Hiệu của hai tập hợp: Tập hợp \(C\) bao gồm các phần tử thuộc \(A\) nhưng không thuộc \(B\) gọi là hiệu của \(A\) và \(B\). Kí hiệu là \(C=A\)\\(B\).
\(A\)\\(B\)\(=\left\{x|x\in A;x\notin B\right\}\)
\(x\in A\)\\(B\) \(\Leftrightarrow\left\{{}\begin{matrix}x\in A\\x\notin B\end{matrix}\right.\)
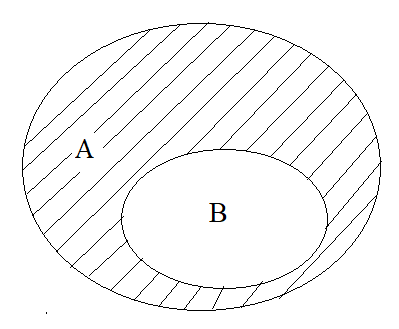
- Khi \(B\subset A\) thì \(A\)\\(B\) gọi là phần bù của \(B\) trong \(A\). Kí hiệu là \(C_AB\).
@70788@
4. Các tập hợp số
- Tập hợp số tự nhiên \(N\) :
\(N=\left\{0,1,2,3,4,...\right\}\)
\(N\)*\(=\left\{1,2,3,4,...\right\}\)
- Tập hợp số nguyên \(Z\): \(Z=\left\{...,-3,-2,-1,0,1,2,3,...\right\}\)
- Tập hợp số hữu tỉ \(Q\):
Số hữu tỉ biểu diễn được dưới dạng phân số \(\dfrac{a}{b}\), trong đó \(a,b\in Z;b\ne0\).
Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Ví dụ: \(\dfrac{5}{4}=1,25;\dfrac{5}{12}=0,41\left(6\right);...\)
- Tập hợp các số thực \(R\):
Tập hợp các số thực bao gồm các số thập phân hữu hạn, vô hạn tuần hoàn và vô hạn không tuần hoàn. Các số thập phân vô hạn không tuần hoàn gọi là số hữu tỉ.
Mỗi số thực được biểu diễn bởi một điểm trên trục số và ngược lại;

- Các tập hợp con thường dùng của \(R\):
+) Khoảng
| \(\left(a;b\right)=\left\{x\in R|a< x< b\right\}\) |
|
| \(\left(a;+\infty\right)=\left\{x\in R|a< x\right\}\) |
|
| \(\left(-\infty;b\right)=\left\{x\in R|x< b\right\}\) |
|
+) Đoạn:
| \(\left[a;b\right]=\left\{x\in R|a\le x\le b\right\}\) |
|
+) Nửa khoảng:
| \([a;b)=\left\{x\in R|a\le x< b\right\}\) |
|
| \((a;b]=\left\{x\in R|a< x\le b\right\}\) |
|
| \([a;+\infty)=\left\{x\in R|a\le x\right\}\) |
|
| \((-\infty;b]=\left\{x\in R|x\le b\right\}\) |
|
5. Số gần đúng. Sai số
- Trong đo đạc, tính toán ta thường chỉ nhận được các giá trị gần đúng.
- Nếu \(a\) là số gần đúng của số đúng \(\overline{a}\) thì \(\Delta_a=\left|\overline{a}-a\right|\) được gọi là sai số tuyệt đối của số gần đúng \(a\).
- Nếu \(\Delta_a=\left|\overline{a}-a\right|\le d\) thì \(-d\le\overline{a}-a\le d\) hay \(a-d\le\overline{a}\le a+d\).
Ta nói \(a\) là số gần đúng của \(\overline{a}\) với độ chính xác \(d\) và quy ước viết gọn là \(\overline{a}=a\pm d\)
- Ngoài ra ta còn dùng tỉ số \(\delta_a=\dfrac{\Delta_a}{\left|a\right|}\), gọi là sai số tương đối của số gần đúng \(a\).
- Quy tắc làm tròn số:
a) Nếu chữ số sau hàng quy tròn nhỏ hơn 5 thì ta thay nó và các chữ số bên phải của nó bởi chữ số 0.
b) Nếu chữ số sau hàng quy tròn lớn hơn hoặc bằng 5 thì ta cũng làm như trên, nhưng cộng thêm một đơn vị vào chữ số của hàng quy tròn.
@1839324@







