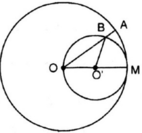
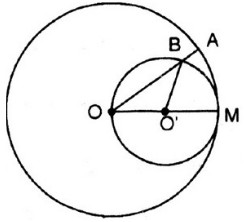
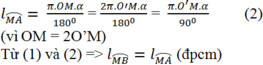cho một đường tròn (O;R) từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB và AC với đường tròn.
a, chứng minh ABOC nội tiếp.
b,D là trung điểm AC và BD cắt đường tròn tại E, AE cắt đường tròn tại F. Chứng minh AB2= AE•AF
c, i là giao điểm ao với (o) chứng minh BC=CF

















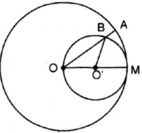
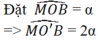 (góc nội tiếp và góc ở tâ của đường tròn (O'))
(góc nội tiếp và góc ở tâ của đường tròn (O'))