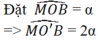 (góc nội tiếp và góc ở tâ của đường tròn (O'))
(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
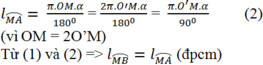

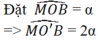 (góc nội tiếp và góc ở tâ của đường tròn (O'))
(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
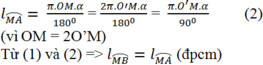
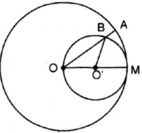
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
Chứng minh cung Ma và cung MB có độ dài bằng nhau
Cho đường trong tâm O bán kính 3cm và một điểm M sao cho OM=5cm. Từ M kẻ tiếp tuyên MA với đường tròn (O) (A là tiếp điểm)
a) Tính độ dài đoạn thẳng AM và giá trị của gicd AMO
b) Qua A vẽ đường thẳng vuông góc với OM tại H,cắt đường tròn(O) tại H,cắt đường tròn(O) tại B(B khác A). Chứng minh MB là tiếp tuyến của đường tròn (O)
c) Kẻ đường kính AC của đường tròn(O). Đường thẳng MC cắt đường tròn tại điểm thứ hai là D. Chứng minh góc MHD bằng góc OCD.
cho đường tròn tâm O bán kính R 2 tiếp tuyến tại A và B của đường tròn cắt nhau tại điểm M đoạn thẳng OM cắt đường tròn (O) tại điểm I , cắt AB tại điểm K a)chứng minh 4 điểm M,A,O,B cùng thuộc đường tròn b)chứng minh OM.OK=R^2 và điểm I là tâm đường tròn nội tiếp tam giác MAB
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM<BM. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn tại D. Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính chiều dài đoạn thẳng AE theo R, r.
Cho đường trong (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC ^ OA. Biết độ dài đường tròn (O) 4π cm. Tính:
a, Bán kính đường tròn (O)
b, Độ dài hai cung BC của đường tròn
cho đường tròn tâm O,bán kính OA .Gọi H là trung điểm của OA ,đường thẳng vuông góc với OA tại H cắt đường tròn tâm O tại B và C . Kẻ tiếp tuyến với đường tròn tâm O tại B cắt đường thẳng OA tại M . Chứng minh OBAC là hình thoi ,tính góc, tính góc BOC biết OM = 2R
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O’). Đường tròn đường kính OC cắt (O) tại M và N. a/ Đường thẳng CM cắt (O’) tại P. Chứng minh: OM//BP. b/ Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. Chứng minh: Tam giác OCD là tam giác cân.
Cho đường tròn tâm O,có bán kính R. Qua điểm M ở ngoài đường tròn, vẽ hai tiếp tuyến MA,MB đến đường tròn(A,B là tiếp điểm).Kẻ đường kính AC của đường tròn tâm O.
a, Chứng minh rằng OM vuông góc với AB, từ đó chứng minh CB song song với OM.
b, Gọi K là giao điểm thứ hai của MC với (O). Chứng minh CK.CM=4R2
c, Chứng minh rằng \(\widehat{MBK}\)= \(\widehat{MCB}\)