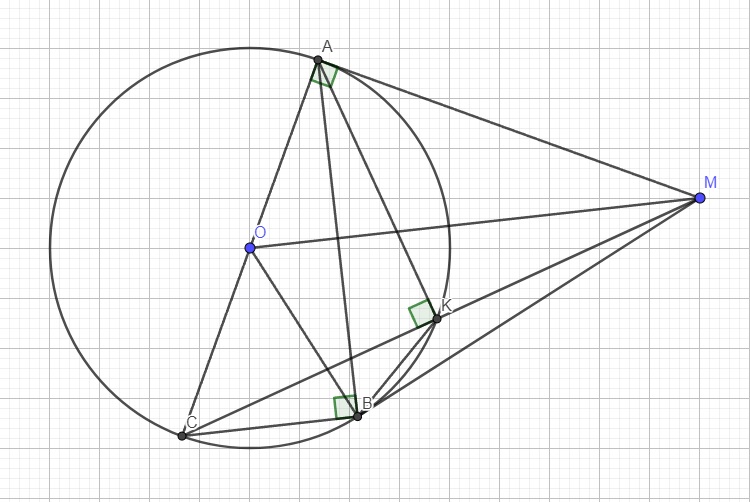
Cho đường tròn tâm O,có bán kính R. Qua điểm M ở ngoài đường tròn, vẽ hai tiếp tuyến MA,MB đến đường tròn(A,B là tiếp điểm).Kẻ đường kính AC của đường tròn tâm O.
a, Chứng minh rằng OM vuông góc với AB, từ đó chứng minh CB song song với OM.
b, Gọi K là giao điểm thứ hai của MC với (O). Chứng minh CK.CM=4R2
c, Chứng minh rằng \(\widehat{MBK}\)= \(\widehat{MCB}\)
a.
Ta có \(MA=MB\) (t/c hai tiếp tuyến cắt nhau)
\(OA=OB=R\)
\(\Rightarrow OM\) là trung trực AB hay OM vuông góc AB
AC là đường kính và B là điểm thuộc đường tròn \(\Rightarrow\widehat{ABC}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ABC}=90^0\Rightarrow AB\perp BC\)
\(\Rightarrow BC||OM\) (cùng vuông góc AB)
b.
Do MA là tiếp tuyến \(\Rightarrow AM\perp AC\) hay tam giác MAC vuông tại A
AC là đường kính và K thuộc đường tròn \(\Rightarrow\widehat{AKC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AKC}=90^0\) hay AK là đường cao trong tam giác vuông MAC
Áp dụng hệ thức lượng:
\(AC^2=CK.CM\Rightarrow CK.CM=\left(2R\right)^2=4R^2\)
c.
Em có nhầm đề ko nhỉ, vì 2 góc này hiển nhiên bằng nhau, ko cần chứng minh, do 1 góc là góc nội tiếp và 1 góc là góc tạo bởi tiếp tuyến và dây cung, cùng chắn cung BK.