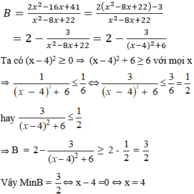tính giá trị nhỏ nhất:A= 2x2-8x-10

Những câu hỏi liên quan
Tính giá trị lớn nhất hoặc nhỏ nhất của các biểu thức sau: A = 2 x 2 - 8 x - 10
A = 2 x 2 - 8 x - 10
= 2 x 2 - 4 x + 4 - 18 = 2 x - 2 2 - 18
Do 2 x - 2 2 ≥ 0 với mọi x ⇒ 2 x - 2 2 – 18 ≥ −18
A = -18 khi và chỉ khi x - 2 = 0 hay x = 2
Do đó giá trị nhỏ nhất của biểu thức A bằng -18 tại x = 2
Đúng 0
Bình luận (0)
Bài 2: Tìm giá trị nhỏ nhất, giá trị lớn nhất (nếu có) của:
a) A = x2 - 4x + 1
b) B = -x2 - 8x + 5
c) C = 2x2 - 8x +19
d) D = -3x2 - 6x +1
a) \(A=x^2-4x+1=\left(x-2\right)^2-3\ge-3\)
\(minA=-3\Leftrightarrow x=2\)
b) \(B=-x^2-8x+5=-\left(x+4\right)^2+21\le21\)
\(maxB=21\Leftrightarrow x=-4\)
c) \(C=2x^2-8x+19=2\left(x-2\right)^2+11\ge11\)
\(minC=11\Leftrightarrow x=2\)
d) \(D=-3x^2-6x+1=-3\left(x+1\right)^2+4\le4\)
\(maxD=4\Leftrightarrow x=-1\)
Đúng 2
Bình luận (0)
a) A = (x-2)^2 - 3 >= -3
--> A nhỏ nhất bằng -3
<=> x = 2
Đúng 1
Bình luận (0)
b) B = -(x+4)^2 + 21 <= 21
--> B lớn nhất bằng 21
<=> x = -4
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị nhỏ nhất của phân thức B = 2 x 2 - 16 x + 41 x 2 - 8 x + 22
Tìm giá trị nhỏ nhất:
a/ P=x2+y2-6x-2y+17
b/ Q=x2+xy+y2-3x-3y+999
c/ R=2x2+2xy+y2-2x+2y+15
d/ S=x2+26y2-10xy+14x-76y+59
e/ T=x2-4xy+5y2+10x-22y+28
Giúp mình với nha!
Tìm giá trị nhỏ nhất của biểu thức A=x4+2x2-8x+2019
Giúp mik vs !!!
\(A=x^4+2x^2-8x+2019\) \(=x^4-2x^2+1+4x^2-8x+4+2014\)
\(=\left(x^2-1\right)^2+4\left(x-1\right)^2+2014\ge2014\forall x\)
" = " \(\Leftrightarrow x=1\)
Đúng 2
Bình luận (1)
Tìm giá trị nhỏ nhất của biểu thức :
A=5+2x2+4y2+4xy-8x-12y
Lời giải:
$A=(x^2+4y^2+4xy)+x^2+5-8x-12y$
$=(x+2y)^2-6(x+2y)+x^2+5-2x$
$=(x+2y)^2-6(x+2y)+9+(x^2-2x+1)-5$
$=(x+2y-3)^2+(x-1)^2-5\geq 0+0-5=-5$
Vậy $A_{\min}=-5$. Giá trị này đạt được khi $x+2y-3=x-1=0$
$\Leftrightarrow x=1; y=1$
Đúng 0
Bình luận (0)
Tìm Gía Trị Nhỏ Nhất:
A=16x2+8x+5
B=x2-x
C=a2-2a+b2+6b+2021
`A=16x^2+8x+5`
`=16x^2+8x+1+4`
`=(4x+1)^2+4>=4`
Dấu "=" xảy ra khi `4x+1=0<=>x=-1/4`
`B=x^2-x`
`=x^2-x+1/4-1/4`
`=(x-1/2)^2-1/4>=-1/4`
Dấu "=" xảy ra khi `x=1/2`
`C=a^2-2a+b^2+6b+2021`
`=a^2-2a+1+b^2+6b+9+2011`
`=(a-1)^2+(b+3)^2+2011>=2011`
Dấu "=" xảy ra khi \(\begin{cases}a=1\\b=-3\\\end{cases}\)
Đúng 1
Bình luận (2)
Tìm giá trị nhỏ nhất của biểu thức :A= 2x2-8x+10
\(A=2x^2-8x+10\)
\(=2\left(x^2-4x+4\right)+2\)
\(=2\left(x-2\right)^2+2\)
Vì \(\left(x-2\right)^2\ge0\Rightarrow A=2\left(x-2\right)^2+2\ge2\)
Dấu "=" xảy ra khi x - 2 = 0 => x = 2
Vậy giá trị nhỏ nhất của A là 2 khi x = 2
Dựa vào hằng đẳng thức để tim giá trị nhỏ nhất trong biểu thức sau: 2x2+ y2+ 2xy- 8x- 6y+ 30
Lời giải:
$2x^2+y^2+2xy-8x-6y+30$
$=(x^2+y^2+2xy)+x^2-8x-6y+30$
$=(x+y)^2-6(x+y)+(x^2-2x)+30$
$=(x+y)^2-6(x+y)+9+(x^2-2x+1)+20$
$=(x+y-3)^2+(x-1)^2+20\geq 20$
Vậy GTNN của biểu thức là $20$ khi $x+y-3=x-1=0$
$\Leftrightarrow x=1; y=2$
Đúng 0
Bình luận (1)